Розділ 3. Вступ до математичного аналізу

Тема 1: Границя функції в точці і на нескінченності. Перша і друга «чудові» границі.

1. Границя функції в точці.

2. Границя функції на нескінченності.

3. Основні теореми про границі функцій.

4. Обчислення границі.

5. «Чудові» границі.

Короткі теоретичні відомості

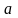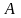Нехай функцію f визначено в деякому околі точки . Число називається границею функції f у точці ,якщо для довільного числа ε >0 існує число 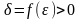таке, що для всіх x , для яких 0<|x-a|<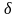 справджується нерівність |f(x)-A| < ε.

Якщо число А є границею функції f у точці а, то це записують так:

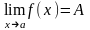(1)

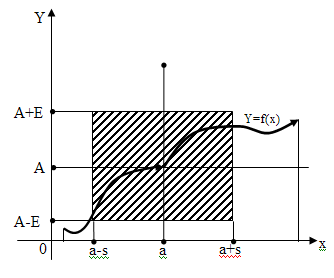Рівність (1) має таке геометричне тлумачення: які б не взяти дві прямі 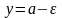та 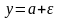(ε>0), знайдуться дві прям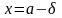і і 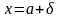(δ>0) такі, що частина графіка функції f, яка відповідає всім точкам xє(а-δ;а+δ),x≠a, потрапляє в середину прямокутника, обмеженого прямими y=A-ε, y=A+ε, x=a-δ та x=a+δ (мал. 1). Що ж до точки (a;f(a)) (якщо в точці а функція f визначена), то вона може належати або не належати цьому прямокутнику. Нехай функція f визначена для всіх х, що задовольняють нерівність |x|>k (x>k,x<-k) при деякому k>0. Ч

Мал. 1.

исло А називається границею функції f при x→∞ (x→+∞, x→-∞), якщо для довільного числа ε >0 існує число M=M(ε)>k таке, що для всіх х для яких |x|>M (x>M, x<-M), виконується нерівність |f(x)-A|<ε.

Символічний запис у цьому випадку такий:

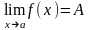(2)

Рівність (2) має таке геометричне тлумачення:

які б не взяти дві прямі y=A-ε та y=A+ε, знайдеться пряма x=M (M≥k , k>0) така, що частина графіка функції f, яка відповідає всім х>M, потрапляє в середину півсмуги, обмеженої прямими y=A-ε , y=A+ε та х=М, що лежить праворуч від прямої х=М (мал. 2).

Мал.2.

Теорема 1.(про представлення функції у вигляді суми своєї границі та нескінчено малої функції).

тоді й тільки тоді, коли 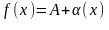, де α(x) – нескінчено мала функція при x→a.

Теорема2 (про границі суми, добутку та частки) Якщо функції і 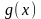визначені в деякому околі точки , можливо , за визначенням самої точки та існують границі 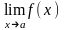, , 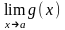то існують границі їх суми (різниці) 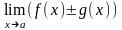, добутку 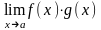, та якщо 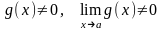, то й частки 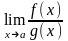та мають місце рівності:

1. ;

2. ;

3. .

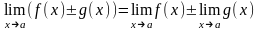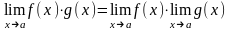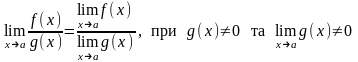Наслідки з теореми 2.

1). Постійний множник можна виносити за знак границі

.

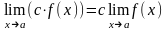2). Границя степеня дорівнює степеню границі

.

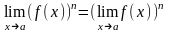Приведемо деякі прийоми обчислення границь на конкретних прикладах.

1). Границя многочлена.

Обчислити .

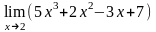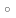Використовуючи теорему 2, отримуємо .

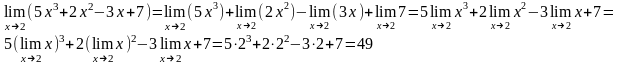Таким чином, для обчислення границі многочлена f(x) при x→x₀ достатньо замість змінної х поставити значення х₀ до якого вона прямує та виконати відповідні дії, тобто .

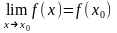2). Границя відношення двох многочленів.

.

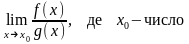а). Якщо g(x₀)≠0 , можна використати теорему про границю частки.

б

x→x₀

). Якщо g(x₀)=0, то теорему про границю частки використати не можна. Тоді якщо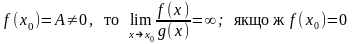 -то маємо невизначеність 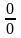. В цьому випадку можна обчислити розкладанням многочленів f(x) і g(x) на множники або заміною y=x-x₀.

П

риклад. Обчислити .

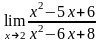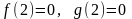. Так як х≠2, маємо .

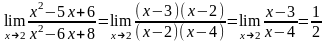3). Граничне відношення многочленів.

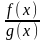при х→∞.

П

риклад. Обчислити .

.

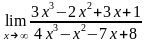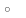
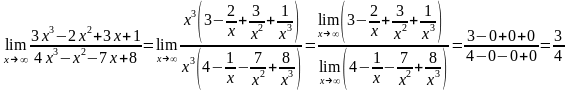4). Границі деяких ірраціональних функцій.

Для обчислення 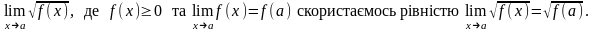(3)

Н

^X→-1

априклад, lim = =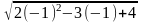 =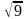3.

Приклад. Обчислити .

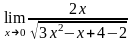Так як 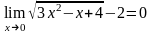, то теорему про границю частки використати не можна. Помножимо чисельник та знаменник на вираз, спряжений до знаменника, отримаємо

l

^x→0

^x→0

^x→0

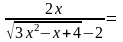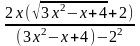im lim =lim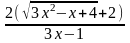 = =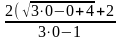-8.

Дуже часто при обчисленні границь використовують «чудові» границі.

I-ша «чудова» границя 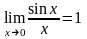(4)

II-га «чудова» границя 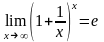(5)

П

риклад. Обчислити .

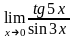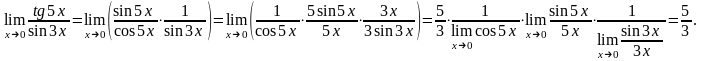
П

риклад. Обчислити .

.
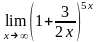
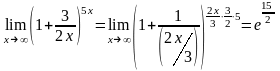