2.1 Примеры решения задач и контрольное задание по разделу колебания Методические указания

При решении задач этого раздела следует добиваться четкого уяснения понятий “амплитуда”, “частота”, “период колебаний”, “фаза”, “разность фаз”. Необходимо обратить внимание на общие закономерности, которые характерны для всех колебательных процессов независимо от их природы. При рассмотрении механических колебаний и волн качественный анализ рекомендуется начинать, как и ранее при изучении поступательного и вращательного движений, с анализа сил, действующих на тело.

При изучении темы “Волны” следует обратить внимание на картину мгновенного распределения смещений в бегущей волне, различие между бегущей и стоячей волнами, условие интерференции волн, перераспределение энергии при образовании максимумов и минимумов интенсивности.

Пример 19.

Материальная точка совершает гармонические колебания с угловой частотой ω. В момент, принятый за начальный, точка имела максимальное отклонение х = х_мах. Написать уравнения для смещения х(t), скорости V(t) и ускорения а(t.)

Решение

Уравнение для смещения при гармоническом колебании можно записать двумя способами:

(1)

, (2)

где А и ω – амплитуда и угловая частота колебаний; t – время; и – начальные фазы, соответствующие форме записи (1) и (2). Обе формы записи эквивалентны и основаны на простой связи между синусом и косинусом:

, .

Если использовать форму записи (1), то начальную фазу можно найти из условия при t = 0. Отсюда имеем , или

Поскольку изменение фазы на 2 не изменяет состояние колебательного движения, то можно считать . По тем же соображениям для формы записи (2) имеем

, или , так что . Подставляя и соответственно в (1) и (2).получим

и . (3)

Найдя 1-ю и 2-ю производные от , получим формулы для скорости и ускорения:

; (4)

. (5)

Сопоставив (3) и (5), имеем .

Таким образом, ускорение максимально в точках максимального отклонения маятника от положения равновесия и в каждый момент времени направлено в сторону, противоположную смещению х.

Пример 20. Точка совершает гармонические колебания с периодом Т=24 с и начальной фазой, равной нулю. Определить, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.

Решение

Уравнение гармонических колебаний имеет вид

x = Asin(ωt + φ_o),

где ω – циклическая частота, связана с периодом ω =2π/T. φ_{o –}начальная фаза, φ_o =0. По условию x(t) =A/2, тогда получим откуда после подстановки или , следовательно, t = 2 c.

Пример 21. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы Е = 0,1мДж. Определить амплитуду А колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение

Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы: , где ω =2π/T. Отсюда амплитуда .

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть определена: F = - kx, где k – коэффициент упругости, x – смещение колеблющейся точки.

Максимальной сила будет при максимальном смещении x_max, равном амплитуде: F_max = kA.

Коэффициент k выразим через период колебаний: , подставив А и k в выражение для F_max после упрощения получим

Произведем вычисления А = и .

Пример 22.

Тонкий обруч, повешенный на гвоздь, вбитый в стенку, колеблется в плоскости, параллельной стене. Радиус обруча равен 30 см. Вычислить период Т колебаний обруча.

Р ешение

О бруч, висящий на гвозде, представляет собой физический маятник. Его период выражается формулой , где - приведенная длина маятника, I –момент инерции маятника относительно оси колебаний, l_c- расстояние от оси до центра масс.

Момент инерции обруча относительно оси, проходящей через центр масс равен I = mR² , для определения момента инерции относительно оси О надо воспользоваться формулой Штейнера I = I_c + ma^2.. В данном случае а является расстоянием l_c и равен R,

тогда I = mR² +mR² =2mR² .

Таким образом, , произведя вычисления, получим

Пример 23.

Однородный стержень длиной L = 0,5 м совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Hайти период колебаний Т стержня.

Решение

Д ля периода колебаний T физического маятника имеем выражение: , где J - момент инерции маятника относительно точки подвеса, m - его масса, a - расстояние между центром масс маятника и осью вращения, g - ускорение свободного падения. Момент инерции стержня относительно перпендикулярной ему оси, проходящей через его конец, равен J = mL²/3. Центр масс стержня совпадает с его серединой, потому a = L/2. Подставив найденные выражения в формулу для периода колебаний, получим: . Подставив численные значения, найдем T=1,16 c.

Пример 24.

Амплитуда колебаний математического маятника длиной L=1 м за время t=10 мин уменьшилась в N=2 раза. Определить логарифмический декремент затухания колебаний Θ.

Решение

Зависимость амплитуды затухающих колебаний от времени имеет вид A(t) = A₀exp(-δt), где A₀ - амплитуда колебаний в момент времени t = 0, δ - коэффициент затухания. Логарифмический декремент затухания Θ определяется следующим образом:

,

где A(t) и A(t+T) - амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на время T, равное периоду колебаний.

П о условию задачи A(t)=A₀/N, откуда получаем и .

П ериод колебаний математического маятника равен: . Подставляя величины T и δ, находим логарифмический декремент затухания:

Используя численные значения, получаем Θ=0,00232.

Пример 25.

Определить максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой A=3 см и угловой частотой ω=π/2 c^-1.

Решение

Уравнение гармонических колебаний имеет вид: x = A cos(ωt+ϕ), где ϕ - начальная фаза колебаний. Скорость движения точки V и ее ускорение a найдем, вычислив производные:

V = dx/dt = -Aω sin(ωt+ϕ) и a = dV/dt = - Aω²cos(ωt+ϕ).

Максимальные значения функций sinx и cosx равны 1. Соответственно, максимальные значения модулей скорости и ускорения точки будут равны: V_max= Aω, a_max = Aω².

Подставляя численные значения, получим V_max= 4,71 см/c, a_max= 7,40 см/c².

Пример 26.

Складываются два колебания одинакового направления, описываемых уравнениями x₁=A₁cosωt и x₂= A₂ cos(ωt+π/3), где A₁=4 см, A₂=2 см. Найти амплитуду результирующего колебания.

Р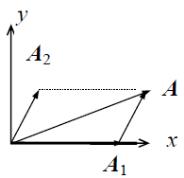 ешение

Для решения задачи удобнее всего использовать метод векторных диаграмм. Диаграмма сложения колебаний показана на рисунке. Так как начальная фаза первого колебания равна нулю, то вектор, соответствующий этому колебанию, направлен вдоль оси абсцисс. Вектор, соответствующий второму колебанию, составляет с осью x угол π/3, равный начальной фазе второго колебания. Амплитуду результирующего колебания находим из треугольника AA₁O по теореме косинусов:

A² = A₁² +A₂² -2A₁A₂cos(π-π/3).

Подставляя численные значения, получим A = 5,3 см.

Пример 27.

Период затухающих колебаний Т = 4 с; логарифмический декремент затухания θ = 1,6; начальная фаза _о = 0. При смещение точки равно х = 4,5 см. Написать уравнение движения этого колебания

Решение.

Затухающее колебание в общем случае описывается уравнением: , (1)

где – параметры, подлежащие определению; ₀ = 0 по условию задачи. Найдем численные значения коэффициента затухания  и частоты затухающих колебаний :

.

Амплитуду определим, исходя из формулы (1):

. (2)

Воспользовавшись начальными условиями, согласно которым х=4,5см при с, получим после подстановки численных значений в (2):

. (3)

Подставив в (1) все найденные числовые значения параметров, запишем искомое уравнение в окончательном виде: .