§3. Дифференциальные уравнения 1 – го порядка

Сведения из теории

Дифференциальное уравнение 1-го порядка (далее везде ДУ)– это уравнение вида , которое содержит переменную , переменную у и переменную . Именно наличие символа указывает на то, что переменная у является функцией переменной , т.е. . Проблема в том, что символ у, так же как и символ являются всего лишь значками функции и ее производной. Нет самого главного – формулы, выражающей через х явно или неявно. Найти эту формулу и означает решить дифференциальное уравнение.

Очень важна другая форма записи дифференциального уравнения – симметрическая или дифференциальная. Она имеет вид

.

Это уравнение описывает зависимость между переменными х, у и их дифференциалами и . Такая запись дифференциального уравнения не навязывает, какую переменную считать независимой, а какую зависимой. Именно поэтому форма называется симметрической. Обе формы дифференциального уравнения легко преобразуются друг в друга с помощью равенства .

Теперь определим, что же является решением ДУ.

Определение Решение ДУ – это функция , которая при подстановке ее в дифференциальное уравнение превращает его в тождественное равенство относительно х, т.е.

.

Необходимо подчеркнуть, что каждому дифференциальному уравнению удовлетворяет не одна функция , а бесконечное множество функций , где С -- произвольная постоянная. Чтобы выделить одно нужное решение достаточно указать какое числовое значение у₀ искомая функция должна принимать при заданном значении х₀.

Задача Коши: найти решение дифференциального уравнения , удовлетворяющее начальным данным . Геометрически это означает – найти такое решение дифференциального уравнения, график которого проходит через точку .

Определение Общим решением ДУ первого порядка называется бесконечное семейство функций , содержащее одну произвольную постоянную и удовлетворяющее двум условиям:

1. при каждом фиксиро­ванном значении С функция является решением ДУ;

2. каково бы ни было начальное условие , можно найти такое значение постоянной С = С₀, при котором функция 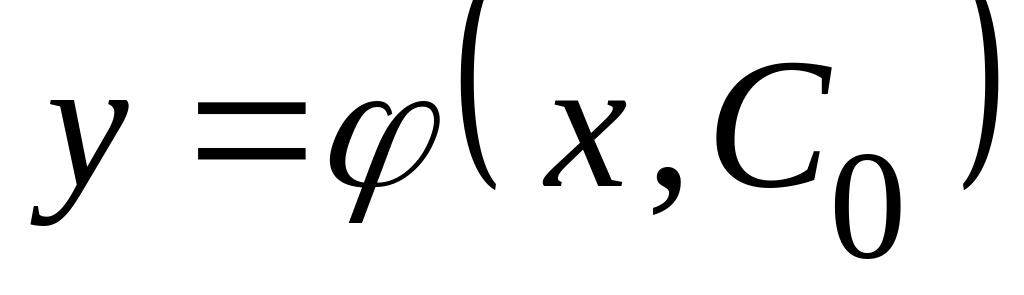удовлетворяет данному начальному условию.

Решение, получающееся из общего при любом конкретном значении , называется частным решением .

Говорят, что найдено общее решение ДУ, если зависимость у от х получена в виде функция (у выражено через х явно с помощью формулы ).

Говорят, что найден общий интеграл ДУ, если зависимость между у и х получена в виде уравнения , где С -- произвольная константа. В этом случае зависит от неявно через уравнение. Иногда можно из этого уравнения выразить у явно через х. Но, как правило, формула получается очень громоздкой. Иногда такое выражение невозможно в принципе.

3.1. Дифференциальные уравнения с разделенными переменными

Сведения из теории

Традиционно изложение методов решения дифференциальных уравнений начинается с уравнений с разделенными переменными. Это обязательно уравнение в симметрической форме, у которого выражение, стоящее перед символом , зависит только от переменной , а выражение, стоящее перед , зависит только от переменной (слово «разделить» здесь означает не арифметическую операцию деления, а процедуру отделения выражений, содержащих только х от выражений, содержащих только у). Короче, уравнение с разделенными переменными имеет вид

.

Перенесем в правую часть слагаемое, содержащее . Получим уравнение . Выражения слева и справа рассматриваем как дифференциалы двух неизвестных функций, каждая из которых зависит только от одной переменной, а именно , а . Если дифференциалы функций равны, то сами функции могут отличаться только на константу. Следовательно, , где - некоторая константа. Как найти функции и ? Да очень просто. -- это какая - либо первообразная для функции , а -- какая - либо первообразная для функции .

Прежде чем рассматривать пример, оговорим одну «вольность», допустимую при решении дифференциального уравнения с разделенными переменными. Пусть уравнение приведено к виду . «Вольность» заключается в том, что можно не переносить слагаемое с переменной у вправо, а сразу взять неопределенные интегралы от всех трех элементов уравнения, а именно . При этом неважно по какой переменной вы возьмете интеграл от нуля: по х или по . Он все равно будет равен константе С.

Подчеркнем конструктивные особенности дифференциального уравнения в симметрической форме:

1. символы и в уравнении должны присутствовать по одному разу;

2. символы и не должны стоять в знаменателе;

3. неважно, в каком порядке следуют слагаемые с и ;

4. лучше, если символы и будут стоять в конце выражений.

Пример16. Найти общий интеграл дифференциального уравнения

.

Решение. Очевидно, что наше уравнение содержит два слагаемых с символом . Это нужно исправить. Перенесем, например, выражение влево, сгруппируем слагаемые с и вынесем символ за скобку, но лучше назад, а не вперед.

 

Проинтегрируем его: . В результате получим уравнение . Очевидно, что переменные х и у входят в это уравнение вперемешку. Переменная у не выражена явно как функция переменной х. Поэтому это уравнение является общим интегралом дифференциального уравнения. Получение этого уравнения можно считать концом решения.

Ответ. Общий интеграл дифференциального уравнения .

Замечание. Если бы в примере 1 требовалось найти общее решение дифференциального уравнения, то получение уравнения не являлось бы концом решения. Для получения общего решения в явном виде нужно из уравнения выразить : .