Замена переменной и интегрирование по частям в определенном интеграле.
Теорема 1.
Пусть на отрезке
задана непрерывная функция
y=f(x)
, и меющая первообразную
F(x)
, и пусть существует функция
,
такая, что
1.
;
2.
….
и…. непрерывны на отрезке
; 3.
непрерывна на отрезке
.
Тогда справедливо равенство
(12.11)
Доказательство.
Таким образом, сравниваем левую и последнюю части, приходим к формуле (12.11).
Как и в случае с
неопределенным интегралом, использование
замены переменной позволяет упросить
исходный интеграл, приблизив его к
табличному. При этом, в отличие от
неопределенного интеграла, нет
необходимости возвращаться к исходной
переменной интегрирования. Достаточно
найти пределы изменения
новой переменной интегрирования t,
когда
.
Замечание.
Как и в случае неопределенного интеграла,
на практике новую переменную вводят
как функцию
.
В этом случае пределы интегрирования
новой переменной находятся совсем
просто:
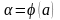
Пример.
Вычислить
Решение.
Пусть
.
Тогда
.
Если
,
то
,
если
,
то
Следовательно,
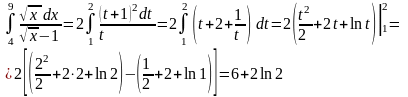
Теорема 2.
Пусть функции
и
непрерывны и имеют производные на
отрезке
.
Тогда
(12.12)
Доказательство.
Как известно,
.
Проинтегрируем то равенство на отрезке
.
Но
,
откуда и следует формула (12.12), которая
называется формулой
интегрирования по частям определенного
интеграла.
Пример.
Вычислить
Решение.
Пусть
,
.
Тогда
,
Применяя формулу (12), получаем
