- •Лекция 11. Неопределенный интеграл
- •11.1 Первообразная и неопределенный интеграл.
- •11.2 Свойства неопределенного интеграла.
- •11.3 Таблица основных интегралов.
- •11.4 Некоторые методы интегрирования. Метод подстановки.
- •Интегрирование некоторых выражений, содержащих в знаменателе квадратный трехчлен.
- •Пример.
- •Метод интегрирования по частям.
- •11.5 Понятия о неберущихся интегралах
- •Лекция 12. Определенный интеграл. Понятие определенного интеграла. Определенный интеграл, как предел интегральной суммы.
- •12.1. Задачи, приводящие к понятию определенного интеграла:
- •12.2. Геометрический и экономический смысл определенного интеграла.
- •12.3. Несобственные интегралы с бесконечными пределами.
- •12.1. Задачи, приводящие к понятию определенного интеграла. Задачи о пути, пройденном точкой при неравномерном движении.
- •Теорема о существовании определенного интеграла.
- •Вычисление определенного интеграла. Формула Ньютона-Лейбница.
- •Дифференцирование определенного интеграла по переменному верхнему пределу (теорема Барроу).
- •Свойства определенного интеграла.
- •Замена переменной и интегрирование по частям в определенном интеграле.
11.2 Свойства неопределенного интеграла.
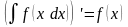 .
.
Действительно, если – первообразная для функции , то
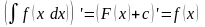 ,
что и требовалось
доказать.
,
что и требовалось
доказать.
 .
. .
.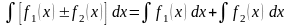 .
.
Докажем это свойство
Найдем
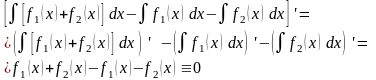
Следовательно
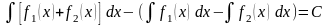
и окончательно
, что и требовалось доказать..
5
 .
.
Доказательство аналогично свойству 4.
6.Инвариантность формулы исследования.
Ф ормула
интегрирования сохраняет вид, если в
нее вместо независимой переменной х
подставить любую дифференцируемую
функцию
ормула
интегрирования сохраняет вид, если в
нее вместо независимой переменной х
подставить любую дифференцируемую
функцию
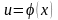 ,
то есть
,
то есть
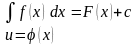
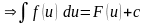
Доказательство.
Пусть
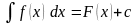 и
– дифференцируемая функция. Рассмотрим
сложную функцию
и
– дифференцируемая функция. Рассмотрим
сложную функцию
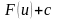 .
.

Примеры.
,
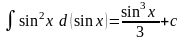 ,
,
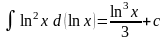
11.3 Таблица основных интегралов.
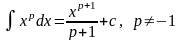 7.
7.
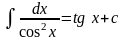
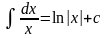 8.
8.

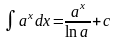 9.
9.

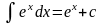 10.
10.

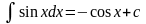 11.
11.
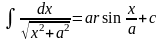
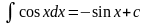 12.
12.
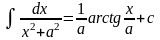
Замечание. Не путать интегралы 9 с 11 и 10 с 12.
Задача успешного интегрирования состоит в умении свети интеграл к табличному.
Примеры.
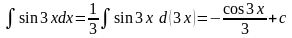

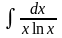
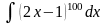
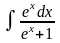


11.4 Некоторые методы интегрирования. Метод подстановки.
Метод подстановки
(или метод замены переменной) – один из
основных методов интегрирования.
Рассмотрим
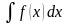 , где
, где
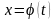 – непрерывная и дифференцируемая
функция. Тогда
– непрерывная и дифференцируемая
функция. Тогда
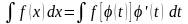 (11.1)
(11.1)
Докажем.
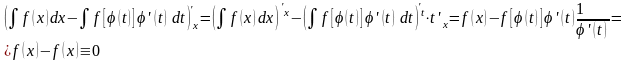 Отсюда
Отсюда
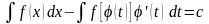
Так как неопределенные интегралы определены с точностью до постоянной, то отбросив указанную постоянную, получим формулу (11.1).
Смысл использования замены - от заданного интеграла перейти к более простому или даже табличному.
Пример 1.
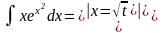
Замечание.
Часто удобно вводить замену
в неявном виде, то есть рассматривать
новую переменную t
как
функцию от х
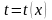 .
.
Пример 2.
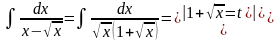 .
.
Пример 3
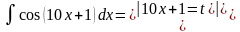 .
.
Интегрирование некоторых выражений, содержащих в знаменателе квадратный трехчлен.
В случае обоих знаков получим табличные интегралы.
2.

Для первого
интеграла введем замену
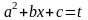 тогда
тогда
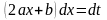 .
.
В результате
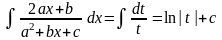 .
.
Окончательно

Пример.
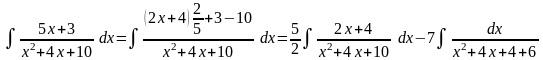
Для первого
интеграла введем замену
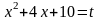 .
.
Тогда
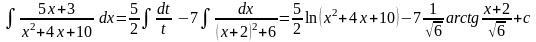
Метод интегрирования по частям.
Пусть
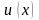 и
и
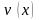 – дифференцируемые функции. Тогда по
свойству дифференциала
– дифференцируемые функции. Тогда по
свойству дифференциала
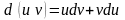 или
или
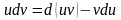
Интегрируя обе части последнего равенства, получаем
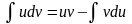 (11.2)
(11.2)
Формула (11.2)
называется формулой
интегрирования по частям
неопределенного интеграла. При
использовании этой формулы разбиение
подынтегрального выражения исходного
интеграла на два сомножителя
u
и dv
осуществляется таким образом, что один
из них u
-
дифференцируется, а второй – dv
-
интегрируется. При этом цель заключается
в том, чтобы новый интеграл
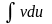 был
проще исходного
был
проще исходного
 .
.
Пример. Найти интегралы
а)
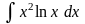 б)
б)
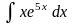
а)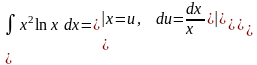
Анализ полученного
решения показывает, что постоянная С1,
полученная при вычислении
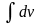 ,
не входит в общее решение. Поэтому можно
считать, что С=0. Это упрощает запись
решения.
,
не входит в общее решение. Поэтому можно
считать, что С=0. Это упрощает запись
решения.
б)

В некоторых случаях формулу интегрирования приходится применять несколько раз.
Пример.
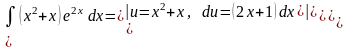
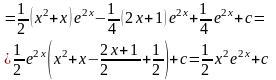
Следует иметь в виду, что по частям находят интегралы типов:
а)
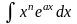 ;
;
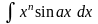 ;
;
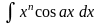 ;
;
б)
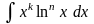 ;
;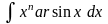 ;
;
 ;
;
в)
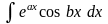 ;
; ,
,
где a, b, k – действительные числа, n – целое положительное число.
При вычислении интегралов группы «а)» принимают xn=u; при вычислении интегралов группы «б)» принимают dv=xkdx.