Интегральное исчисление
Интеграл - одно из важнейших математических понятий. Он широко применяется во многих отраслях науки, техники, экономики; имеет мировоззренческое значение.
Цель: показать, что операция дифференцирования имеет обратную операцию – интегрирование. Эта операция неоднозначная, что следует из геометрического смысла неопределенного интеграла.
Задача: научиться различать является ли данный интеграл табличным (околотабличным); овладеть способами интегрирования, позволяющими сложные интегралы сводить к табличным.
Лекция 11. Неопределенный интеграл
1
1.1.
Понятие первообразной и неопределенного
интеграла
11.2. Свойства неопределенного интеграла.
11.3. Таблица интегралов.
11.4. Некоторые методы интегрирования:
- метод подстановки;
- интегрирование некоторых выражений, содержащих в знаменателе квадратный трехчлен;
- интегрирование по частям.
11.5. Понятие о неберущихся интегралах.
11.1 Первообразная и неопределенный интеграл.
При решении многих
задач физики, математики требуется по
заданной функции
найти ее производную
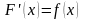Но достаточно часто приходится сталкивать
с обратными задачами, когда по известной
производной
требуется найти саму функцию
.
Н
апример,
по закону измерения скорости V=V(t)
необходимо найти закон движения S=S(t).
Но
.
Таким образом, по
известной производной
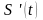следует найти функцию
.
О
пределение.
Операция отыскания функции по ее
производной называется интегрированием,
а раздел математики, изучающий способы
интегрирования функций – интегральным
исчислением.
Определение.
Функция
,
определенная на промежутке
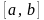называется
первообразной
для функции
на том же отрезке,
если для любого
имеет место
равенство
Примеры.
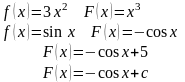
Очевидно, что если
- первообразная для функции
, то
,
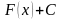где
есть также первообразная той же функции.
Действительно,
пусть
,
но и
.
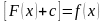Вывод: если функция имеет хотя бы одну первообразную, то для нее существует бесчисленное множество первообразных.
Теорема 11.1.
Если некоторая первообразная функции , то выражение ,
где С – произвольная постоянная величина, исчерпывает множество всех
первообразных функции на данном промежутке.
Доказательство.
Пусть
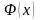наряду с
есть первообразная функции
.
Это означает, что:
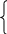
отсюда
,
то есть
,
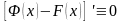или
.
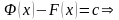
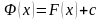иными словами, любые первообразные функции отмечаются на постоянную величину.
Ф
ункция
имеющая на некотором промежутке
первообразную, называется интегрируемой
на этом промежутке.
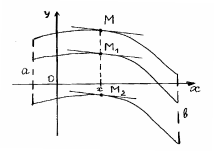
Определение. Множество всех первообразных для функции на данном промежутке называется неопределенным интегралом и обозначается следующим образом
– подынтегральная функция
– подынтегральное
выражение
Очевидно,
операция интегрирования ставит
соответствие функции
бесчисленное множество функций
(первообразных)
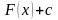или говорят семейство функций.
О
Рис. 11.1
тыскание первообразной для функции означает нахождение уравнения кривой по известному в каждой ее точке угловому коэффициенту касательной. Очевидно, в силу произвольности С таких кривых существует бесчисленное множество. Геометрически это объясняется тем, что в каждой задается лишь направление касательной, а не сама касательная. Каждая кривая получается с параллельным любой из них вверх (вниз). Каждая из кривых называется интегральной кривой.Таким образом, с геометрической точки зрения неопределенный интеграл представляет собой бесчисленное множество (или семейство) интегральных кривых.
Пример
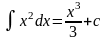– семейство
кубических парабол.
Теорема существования неопределенного интеграла. Если
подынтегральная функция непрерывна на некотором отрезке, то она на
нем интегрируема.