Методическое пособие по ТАУ / 8 / 77-89
.DOC
4. ОЦЕНКА КАЧЕСТВА УПРАВЛЕНИЯ.
СТАБИЛИЗАЦИЯ И КОРРЕКЦИЯ
4.1. Показатели качества
Как всякая динамическая система, САУ может находиться в одном из двух режимов - стационарном (установившемся) и переходном. Стационарный режим может быть двух типов: статический и динамический. Ограничимся здесь рассмотрением лишь статического режима.
В статическом режиме, при котором все внешние воздействия и параметры системы не меняются, качество управления характеризуется точностью.
Рассмотрим САУ с
двумя воздействиями: задающим
и возмущающим
.
Структурная схема такой САУ приведена
на рис.4.1, где обозначено: 1 - участок
системы от входа до точки приложения
возмущения; 2 - участок системы от точки
приложения возмущения до выхода с
передаточной функцией
;
3 - цепь обратной связи.
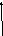
1
2
3
Рис.4.1
В операторной форме САУ описывается уравнением динамики:
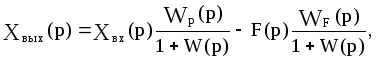
где
-
передаточная функция разомкнутой САУ,
-
передаточная функция разомкнутой цепи.
Уравнение статики получается из уравнения динамики при подстановке в последнее р=0, что соответствует постоянству всех переменных, то есть равенству нулю их производных.
В рассматриваемом примере уравнение статики принимает вид:
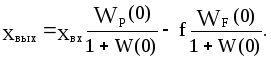
Вид
и
зависит от того, содержатся ли в системе
интегрирующие звенья или нет. Рассмотрим
вначале случай, когда интегрирующие
звенья отсутствуют (такие САУ называются
статическими).
В случае статической
системы
и
так как знаменатели передаточных функций
всех звеньев, входящих сомножителями
в выражения
и
при р=0 обращаются в единицу.
В результате получим:
(4.1)
Статическая
характеристика
неоднозначна из-за наличия возмущения
f. Статическая ошибка
при неизменном задающем воздействии
определяется выражением:
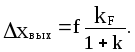
Для разомкнутой САУ уравнение статики будет иметь вид
а статическая ошибка относительно замкнутой системы увеличивается в (1+k) раз:
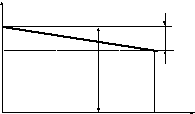
График зависимости выходной величины САУ от возмущения обычно называется внешней характеристикой, которая в общем виде представлена на рис.4.2.
0 1max f
Рис.4.2
В различных областях техники точность в установившемся режиме принято характеризовать величиной отклонения выходной координаты в полном диапазоне изменения возмущающего воздействия в следующем виде:
1) абсолютной
величиной отклонения. Например:
.
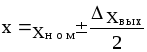Под номинальным
значением
понимается усредненное значение выходной
величины;
2) относительной величиной отклонения, выраженной в процентах. Например:
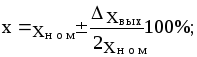(4.2)
3) статизмом внешней характеристики S, определяемым выражением
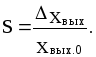
Наличие статической ошибки в общем случае является нежелательным, так как создается погрешность управления. Но для полного устранения статического отклонения требуется до бесконечности увеличивать коэффициент передачи k, что нереализуемо по ряду причин (например, по условию обеспечения устойчивости). Таким образом, в статической САУ принципиально нельзя полностью устранить статическую ошибку.
Но вместе с тем имеется путь устранения статической ошибки при конечной величине коэффициента передачи.
Введем в рассмотренную статическую САУ интегрирующее звено, причем так, чтобы оно находилось на участке 1 структурной схемы (см. рис.4.1), т.е. между точками приложения задающего и возмущающего воздействий. Теперь САУ будет описываться уравнением динамики
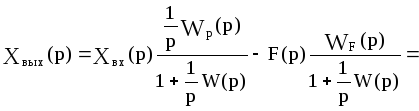
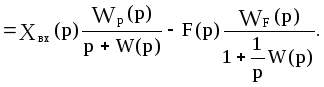
Подставив в это выражение значение р=0, получим уравнение статистики:
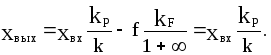
Отсюда следует, что при включении интегрирующего звена в оговоренный выше участок системы удалось полностью ликвидировать статическую ошибку, то есть получить S=0.
САУ, в которых при стремлении возмущающего воздействия к постоянной величине, отклонение выходной величины стремится к нулю и не зависит от величины приложенного воздействия, называются астатическими.
Если интегрирующее звено включить не в оговоренный выше участок структуры, а, например, в цепь обратной связи, то получим
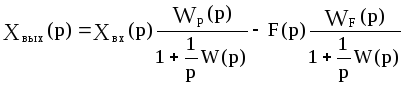
и уравнение статики
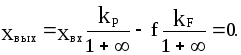
Практический смысл такая система потеряла.
В другом случае, если интегрирующее звено включить на участке 3 структуры (т.е. после точки приложения возмущения), действуя аналогично, выведем:
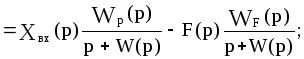
То есть система не является астатической.
Для характеристики переходного режима наибольшее распространение имеют следующие показатели качества: время переходного процесса, перерегулирование, колебательность.
Время переходного процесса характеризует быстродействие системы. Определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становится меньше определенной достаточно малой величины. Обычно это пять процентов.
Перерегулированием
называется максимальное отклонение
выходной величины
на интервале переходного процесса от
установившегося после окончания
переходного процесса значения
,
выраженное в процентах:
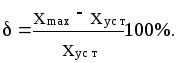
Колебательность характеризуется обычно числом колебаний переходной характеристики за время переходного процесса. В зависимости от характера затухания различают следующие типы переходных характеристик: монотонная (нет ни одного колебания); апериодическая (не более одного колебания); колебательная (несколько колебаний).
Пример 4.1.
Рассчитать
статическую точность системы стабилизации
выходного напряжения генератора
постоянного тока (см. рис.1.3) при следующих
значениях параметров и воздействий:
А/В;
В/А;
;
Ом;
В;
А.
Прежде всего, необходимо составить уравнение статики рассматриваемой системы. Не зная передаточных функций отдельных элементов и системы в целом, составим математическое описание для установившегося режима на основе статических характеристик отдельных элементов (примем допущение, что все элементы имеют линейные статические характеристики).
В разомкнутой системе (см. рис.1.2), как было выведено в подразделе 1.2,
(а)
Э.д.с. генератора
пропорциональна току возбуждения, т.е.
,
где
- коэффициент пропорциональности,
зависящий от материала магнитопровода
генератора, конструктивных особенностей
генератора и т.д.
Ток возбуждения,
в свою очередь, пропорционален входному
сигналу усилителя У, т.е.
,
где
- коэффициент передачи функционального
усилителя У.
С учетом этого соотношение (а) можно записать в следующем виде:
(б)
Уравнению (б) соответствует структурная схема, представленная на рис.4.3.
Рис.4.3
В замкнутой схеме (см. рис.1.3) часть выходного напряжения сравнивается с задающим и разность этих напряжений подается на вход усилителя У, в соответствии с чем можно записать
(в)
где
- коэффициент передачи делителя.
С учетом формулы (в) на основе структурной схемы разомкнутой системы составим структурную схему замкнутой системы, как показано на рис.4.4.
Рис.4.4
С учетом правил преобразования структурных схем для схемы на рис. 4.4 получим уравнение:
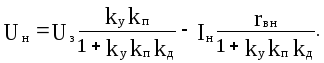(г)
Уравнение статики (г), как видим, полностью соответствует обобщенному уравнению (4.1), отличаясь лишь обозначениями.
Подставим в
уравнение (г) заданные значения величин
и определим максимальное
и минимальное
значение
выходного напряжения, соответствующие
соответственно минимальному (
А) и максимальному (
А) токам нагрузки:
В;
В.
Представим выходное напряжение в форме (4.2):
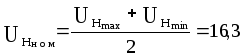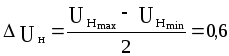В;
В;
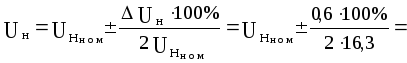
Таким образом, при изменении в оговоренном диапазоне возмущающего воздействия (тока нагрузки) отклонение выходного напряжения не превысит величины 1,84% от номинального значения.
4.2. Критерии качества переходного процесса
Исчерпывающее представление о качестве переходного процесса дает, естественно, сама кривая процесса. Однако при разработке САУ необходимо иметь возможность судить об основных показателях качества переходного процесса без построения их кривых, по каким-либо косвенным признакам, которые определяются более просто и, кроме того, позволяют связать показатели качества непосредственно со значениями параметров САУ. Такие косвенные признаки называются критериями качества переходного процесса.
Существуют три группы критериев качества: частотные, корневые и интегральные.
Наибольшее распространение получили частотные критерии, в основу которых положено использование частотных характеристик. Для иллюстрации возможности оценки качества переходного процесса по частотным характеристикам установим точную аналитическую зависимость между переходной характеристикой h(t) и вещественной частотной характеристикой (ВЧХ) P().
На основании возможности разложения функции времени в ряд Фурье единичное ступенчатое воздействие можно представить в виде выражения
то есть суммы
постоянной составляющей и бесконечного
числа синусоид частотой
и амплитудой
при изменении
от 0 до .
Уравнение АФЧХ имеет вид:
где
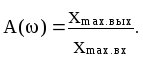
Если на вход системы
подать 1(t), то каждому из входных
синусоидальных колебаний
будет соответствовать колебание на
выходе [с амплитудой
,
сдвинутое по фазе относительно входного
колебания на угол ]
Постоянной
составляющей
на входе будет соответствовать постоянная
составляющая
на выходе.
Результирующее значение выходной величины:
(4.3)
Так как воздействие 1(t) подается в момент t=0, то при t<0:
Уравнение (4.3) при подстановке значения (t) вместо t примет вид:
(4.4)
Вычтем из уравнения (4.3) уравнение (4.4):
t>0.
(4.5)
Пользуясь зависимостью (4.5), можно составить предварительное приближенное суждение о качестве переходной характеристики по виду ВЧХ. Различные типы ВЧХ представлены на рис.4.5.
Р()
Р(0)
3
2
1
4
0
Рис.4.5
Основные положения оценки качества по ВЧХ сводятся к следующему:
1) приблизительно одинаковым частотным характеристикам соответствуют приблизительно одинаковые переходные характеристики;
2) значение переходной характеристики h(t) в установившемся состоянии подчиняется следующему соотношению
3) если ВЧХ имеет вид кривой 1 (см. рис.4.5), переходная характеристика будет монотонной;
4) для ВЧХ, имеющей вид кривой 2, характерно наличие перерегулирования у переходной характеристики величиной 18%;
5) наличие экстремума
ВЧХ (кривая 3) увеличивает колебательность
до величины
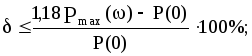
6) наличие экстремума ВЧХ в отрицательной области (кривая 4) приводит к дополнительному росту колебательности:
,
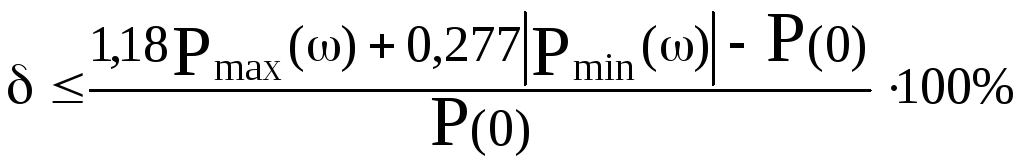где
- величина экстремума ВЧХ в отрицательной
области;
7) длительность
переходного процесса
оценивается приблизительно по величине
интервала существенных частот cщ
(в этом интервале Р()
0,05 Р(0), причем
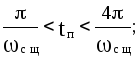
8) острый пик ВЧХ
при
свидетельствует о медленно затухающих
колебаниях с частотой, близкой к
;
9) если при некоторой частоте ВЧХ претерпевает разрыв, то САУ является неустойчивой.
Колебательность переходной характеристики можно оценить по величине относительного максимума амплитудной частотной характеристики А(), примерный вид которой представлен на рис.4.6.
A()
A(0)
Рис.4.6
Величина относительного максимума называется показателем колебательности М и определяется отношением
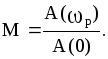
При М<1 переходная
характеристика неколебательна. Чем
больше М, тем больше колебательность.
При М
- незатухающие колебания. Оптимальным
обычно считается М=1,3-1,5. При этом
переходная характеристика имеет слабую
колебательность с частотой, близкой к
.
Вследствие
предельной простоты построения ЛАЧХ
удобно пользоваться именно этой
характеристикой. Информацию здесь несет
среднечастотная часть характеристики.
При частоте среза
наклон ЛАЧХ должен составлять минус 20
дБ/дек, а значение
определяется временем переходного
процесса
и перерегулированием :
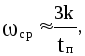
где k берется по графику на рис.4.7 в зависимости от величины .
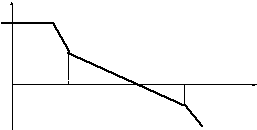
Сопрягающие частоты
ЛАЧХ слева и справа от
,
как показано на рис.4.8, рассчитываются
по выражениям:
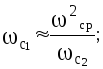
k 4
-
3
2
1
0
-
10
20
30
40
Рис.4.7
G
20
дБ/дек
lg
lg
lg
Рис.4.8
Величины наклонов
ЛАЧХ слева от
и справа от
на качество
переходного процесса почти не влияют.