Звенья второго порядка.

В общем случае описываются уравнением

Перейдем к изображениям по Лапласу:

Отсюда определяем передаточную функцию:

Однако общепринята запись передаточной функции звеньев второго порядка в другом виде:

где

Звенья второго порядка, таким образом, характеризуются тремя параметрами. Это коэффициент передачи, постоянная времени и коэффициент демпфирования . В зависимости от величины коэффициента демпфирования различают типы звеньев: колебательное (0<<1), консервативное (=0) и апериодическое второго порядка (1).

Рассмотрим свойства колебательного звена. Выражения для его частотных функций имеют следующий вид:

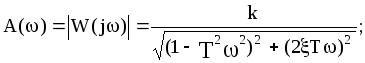
Асимптотическая ЛАЧХ строится тем же приемом, что и для апериодического звена. В области низких частот T<<1 и в подкоренном выражении всеми членами, кроме 1, можно пренебречь. Тогда низкочастотная асимптота G()_нч принимает вид

G()_нч 20lgk.

В области высоких частот ( и в подкоренном выражении можно оставить лишь , пренебрегая остальными членами. Высокочастотная асимптота G()_вч описывается формулой:

G()_вч20lgk20lg(T)²=20lgk40lgT.

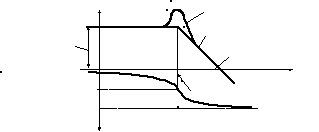
Эта асимптота имеет наклон минус 40 дБ/дек. Сопрягаются асимптоты на частоте , как показано на рис.2.17.

G() Точная ЛАЧХ

Асимптотическая ЛАЧХ

20lgk

40 дБ/дек

0 lg

lg 1/T



Рис.2.17

Точная ЛАЧХ несколько отличается от асимптотической . Максимальная ошибка - в районе около сопрягающей частоты. Для упрощенных расчетов можно считать, что наибольшая ошибка будет при :

В районе точная ЛАЧХ идет ниже асимптотической при и выше - при . При значениях ошибка становится существенной (более трех децибел) и ее необходимо учитывать, используя приведенную выше формулу либо поправочные кривые из справочной литературы.

Представление о динамических свойствах звена можно получить из переходной характеристики, представленной на рис.2.18.

h(t)

k

0 t

Рис.2.18

Примером звена второго порядка может служить колебательный контур (см. схему на рис.2.5 и вывод передаточной функции в примере 2.4).

Консервативное звено - частный случай колебательного звена, когда отсутствует демпфирование. Если обратиться к приведенному выше примеру (см. рис.2.5), то должны отсутствовать потери в контуре (выполняться условие R=0). В этом случае колебания стали бы незатухающими, и переходная характеристика описывалась бы выражением:

На сопрягающей частоте ЛАЧХ консервативного звена имеет всплеск бесконечной амплитуды, т.е. претерпевает разрыв, а ЛФЧХ из нулевого значения скачком достигает значения минус .

При   1 передаточную функцию звена второго порядка можно преобразовать следующим образом:

где

То есть апериодическое звено второго порядка не является типовым или элементарным, так как его можно представить двумя последовательно соединенными более простыми звеньями - апериодическими первого порядка.