Апериодическое (первого порядка) звено.

Описывается дифференциальным уравнением

Перейдя к изображениям, получим:

Передаточные и частотные функции:

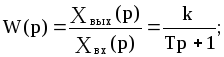
ЛАЧХ звена показано на рис.2.14. Но эта же характеристика может быть представлена приближенно ломаной линией, которая показана на том же рисунке. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика составлена из двух асимптот, к которым стремится ЛАЧХ при  и .

G() асимптотическая ЛАЧХ

20lgk 20дБ/дек

точная ЛАЧХ

lg



Рис.2.14

При малых значениях  можно считать , то есть , следовательно

Соответственно характеристика представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 20 lgk. Это есть первая асимптота, к которой стремится ЛАЧХ при .

С другой стороны, на больших частотах

В этом случае характеристика представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении  на декаду, т.е. в 10 раз,

Таким образом, величина уменьшилась на 20 lg10, т.е. на 20 дБ. Эта линия является асимптотой, к которой стремится ЛАЧХ при . Обе асимптоты пересекаются в точке, соответствующей частоте Поэтому эта частота называется сопрягающей частотой.

Максимальное расхождение между точной () и асимптотической () ЛАЧХ наблюдается при частоте, равной сопрягающей.

Вычислим это расхождение, подставив в соотношения для и значения сопрягающей частоты :

дБ.

От параметров звена рассматриваемая величина не зависит.

На этом же рисунке показана и ЛФЧХ: при  значение  изменяется от 0 до минус . При этом в точке имеем .

АФЧХ представляет собой полуокружность с радиусом в четвертом квадранте комплексной плоскости и центром в точке (, j0) на действительной оси.

Переходная функция, согласно решению уравнения звена, при и нулевых начальных условиях имеет вид

а импульсная переходная функция

Переходная характеристика представлена на рис.2.15.

h(t)

k

0 T t

Рис.2.15

Динамические свойства звена характеризуются постоянной времени Т. Постоянная времени может быть определена как время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

Коэффициент передачи k определяет свойства звена в установившемся режиме.

Очевидно, имея в распоряжении частотные либо переходные характеристики, полученные, например, экспериментально, можно восстановить передаточную функцию звена.

В рассмотренных выше примерах по определению передаточных функций схемы на рис.2.2; рис.2.3; рис.2.6, а являются апериодическими звеньями.

Пример 2.6.

Асимптотическая ЛАЧХ апериодического звена имеет частоту среза . Коэффициент передачи звена k=10. Требуется определить постоянную времени Т.

Нужно на графике или мысленно провести из точки на оси частот прямую с наклоном минус 20 дБ/дек до пересечения с горизонталью, проведенной на уровне . Координата точки пересечения по оси частот даст логарифм сопрягающей частоты , отсюда и с.

Форсирующее (идеальное) звено.

Часто в литературе именуется как пропорционально-дифференцирующее. Выходная величина этого звена пропорциональна входной и производной от входной величины. Передаточная функция и основные частотные функции:

Звено характеризуется двумя параметрами-коэффициентом передачи k и постоянной дифференцирования . В начальный момент времени переходная характеристика, как и у идеального дифференцирующего звена, должна иметь скачек бесконечной амплитуды.

ЛФЧХ форсирующего звена точно такая же, как и у апериодического, только фаза имеет положительные значения.

Низкочастотные асимптоты ЛАЧХ форсирующего и апериодического звеньев совпадают, но высокочастотная асимптота ЛАЧХ форсирующего звена имеет наклон плюс 20 дБ/дек. Сопрягающая частота . Логарифмические частотные характеристики форсирующего звена приведены на рис. 2.16

G() 

Рис. 2.16