2. Отже, f – проективне перетворення

Лема 2 Якщо проективнІ перетворення f₁ і f₂ три точки прямої d переводять відповідно у точки (тобто =А^! …..) то і =М^! (де М –довільна точка прямої d)

Нехай f₁ : f₂ :

(АВ,СМ^/)=(АВ,СМ^//), М^/=М^//.

Теорема Нехай і - довільні репери проективної площини. Тоді існує одне і тільки одне проективне перетворення, яке переводить репер R в репер R^!. При цьому точка з даними координатами в репері R переходить в точку з тими ж координатами в репері

За лемою 1 (Можна задати) : перетворення f, при якому відповідні точки мають однакові координати відносно своїх реперів, буде проективним.

Залишається довести, що це перетворення f єдине.

Доведемо методом від супротивного.

За умовою Нехай

Проведемо довільну пряму , що перетинає сторони координатного трикутника А₁ А₂А₃.

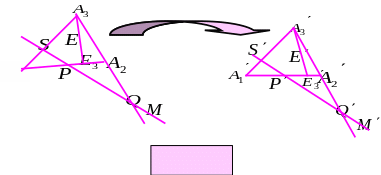
d

Маємо: , Р А₁А₂, За лемою 2 : , Р^/ .

Аналогічно

(лема 2)

Отже, . Тому - єдине проективне перетворення, яке репер R переводить в репер R^/

Властивості проективних перетворень

При проективному перетворенні:

-три точки, які не лежать на одній прямій, переходять у три точки, які не лежать на одній прямій.

-будь-який репер переходить в репер.

-пряма переходить в пряму.

-пучок прямих переходить у пучок прямих.

-зберігається складне відношення 4^х точок прямої, чотирьох прямих пучка.

-Будь-яке проективне перетворення задається парою реперів.

Гомологія

Означення Нетотожне проективне перетворення площини , яке має три інваріантні точки, що лежать на одній прямій, називається гомологією

Властивості гомології

1)Якщо три точки прямої є інваріантними при гомології, то і всі точки цієї прямої є інваріантними

f – гомологія,

Оскільки f проективне, то

Отже, пряма g є прямою інваріантних точок. Ця пряма називається

віссю гомології

2) Пряма, що з’єднує відповідні точки при гомології, є інваріантною прямою.

М

М₀ g g – вісь гомології f

М^/

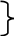
Отже, пряма - є інваріантною прямою.

3). Прямі, що з’єднують відповідні точки при гомології, належать одному пучку, центр якого є інваріантною точкою.

f – гомологія, g – вісь гомології

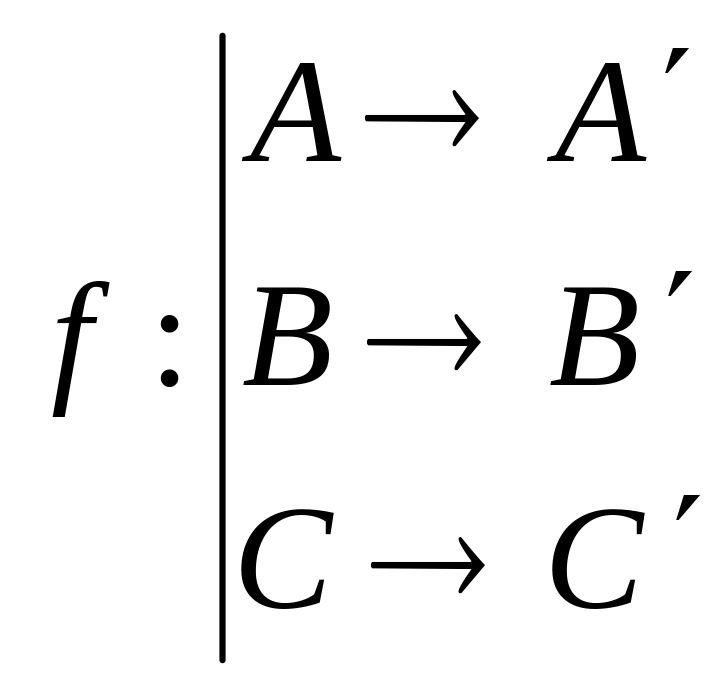
Нехай

Припустимо

З а властивістю 2

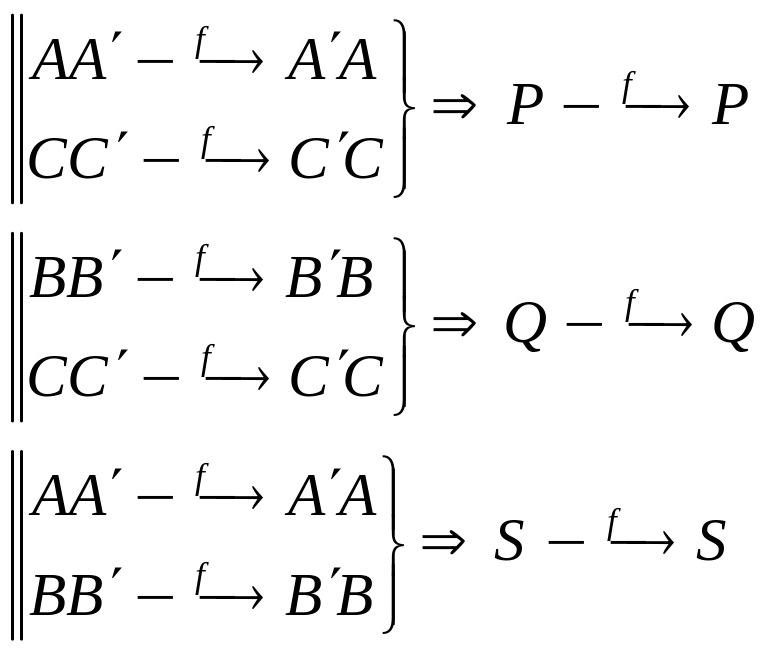
Точки P, Q, S, T –інваріантні і загального положення

- тотожнє,

що суперечить означенню гомології

Отже,

Зауваження: Точка перетину прямих, які проходять через відповідні точки при гомології, називається центром гомології.

Центр осі – гомологія гіперболічна . Центр осі – гомологія параболічна

4). Відповідні прямі при гомології перетинаються в точці, яка належить осі гомології.

S

f – гомологія

А

В

P q

А^! В^!

Нехай

,

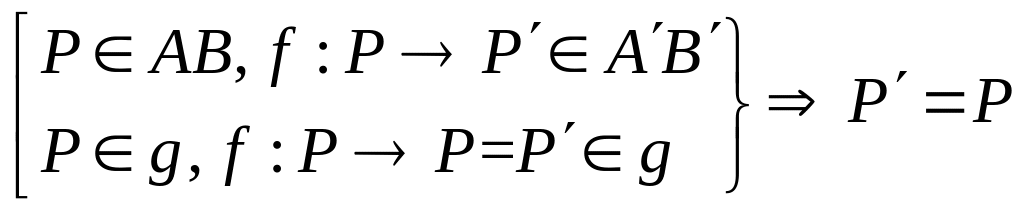Зауваження:

Гомологія задається центром, віссю та парою відповідних точок або іншими елементами, з яких можна знайти центр, вісь і пару відповідних точок