
- •Тема 6: Складне відношення 4-х точок прямої.
- •Складне відношення 4 точок прямої
- •Питання для самоперевірки.
- •Тема7: Проективні перетворення площини.
- •2. Отже, f – проективне перетворення
- •Властивості проективних перетворень
- •Гомологія
- •Властивості гомології
- •Аналітичне задання проективного перетворення площини
- •Питання для самоперевірки.
- •Тема 8: Проективні і перспективні відображення прямих і пучків.
- •Питання для самоперевірки.
- •Тема 9: Лінії другого порядку на проективні площині.
- •Лінії другого порядку.
- •П итання для самоперевірки.
- •Тема10: Перетини лінії другого порядку з прямою.
- •Питання для самоперевірки.
Тема 6: Складне відношення 4-х точок прямої.
М ета:
Ввести поняття складного відношення
4-х точок прямої, довести їх властивості;
розглянути повний чотирьохвершинник,
довести теореми про існування гармонічних
точок, гармонічних прямих у повному
чотирьох -вершиннику.
ета:
Ввести поняття складного відношення
4-х точок прямої, довести їх властивості;
розглянути повний чотирьохвершинник,
довести теореми про існування гармонічних
точок, гармонічних прямих у повному
чотирьох -вершиннику.
План
Означення складного відношення 4-х точок прямої.
Властивості складного відношення 4-х точок прямої
Складне відношення 4-х прямих пучка.
Знаходження складного відношення 4-х точок прямої через їх координати відносно репера на площині.
Повний чотирьохвершинник. Існування гармонічних точок та гармонічних прямих у повному 4-хвершиннику.
Ключові слова: складне відношення 4-х точок прямої, складне відношення 4-х прямих пучка, подвійне відношення, ангармонічне відношення, просте відношення трьох точок, гармонічне відношення 4-х точок, повний 4-вершник, , діагональні точки, діагоналі, четвірка гармонічних точок .
Складне відношення 4 точок прямої
Д ано
ано
![]()
![]()
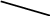 А
(
А
(![]() )
)
 В
(
В
(![]() )
R
)
R
С
(![]() )
)
D
(![]() )
)
Озн-я: Складним, або подвійним, або ангармонічним відношенням чотирьох точок А, В, С, D прямої називається число, яке позначається (АВ,СD)
і
обчислюється так
![]() де (АС),
(ВD)...-визначники,
складені
з координат точок
де (АС),
(ВD)...-визначники,
складені
з координат точок
Властивості:
1.
![]() ,
,
![]()
Якщо у складному відношенні 4-х точок поміняти пари букв місцями, то...
2.
,
![]()
Якщо у складному відношенні 4-х точок поміняти місцями букви в одній парі, то…
3. Нехай
А,
В, С, D
![]() d
,
d
,
![]()
![]()
![]() d
d
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
-
(АС)=
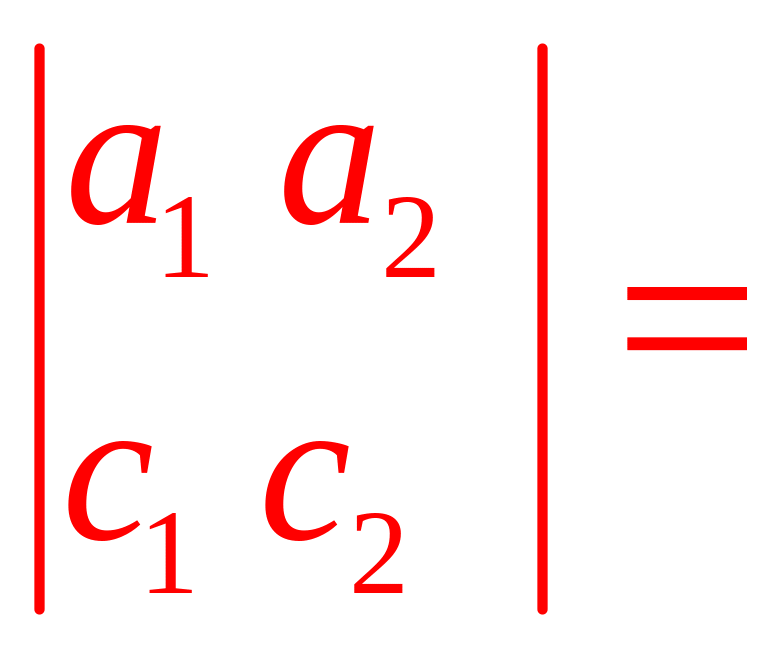
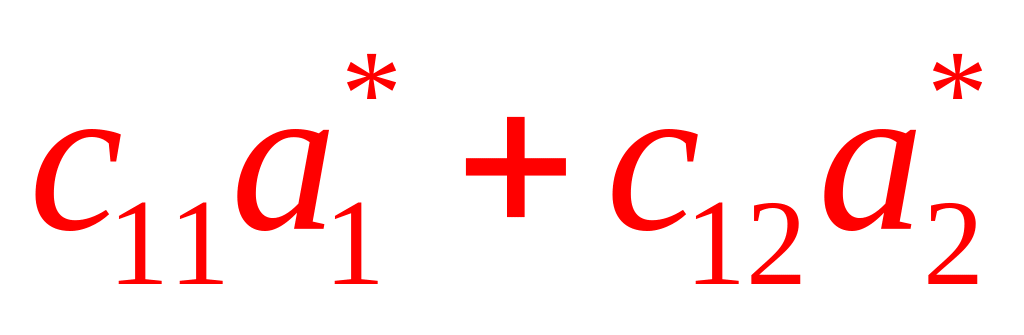
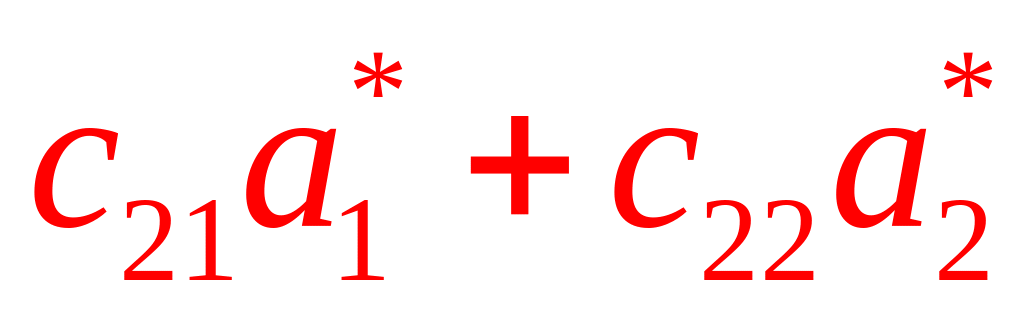
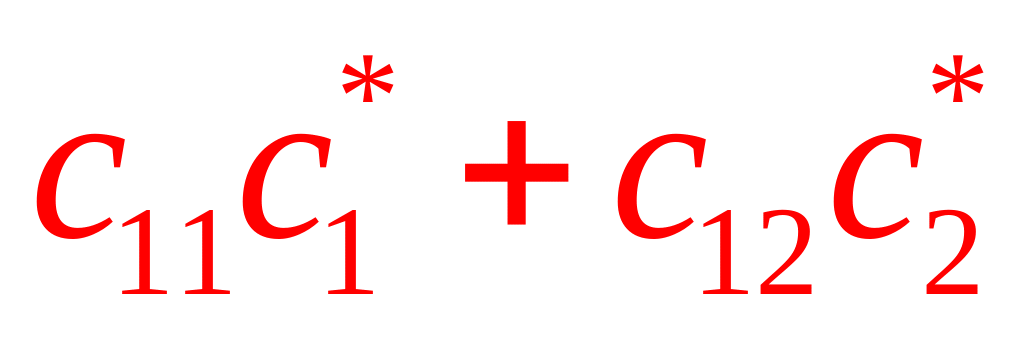

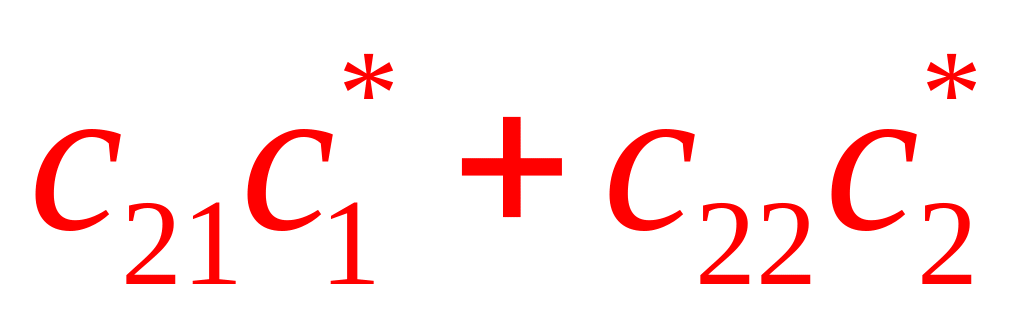
![]()
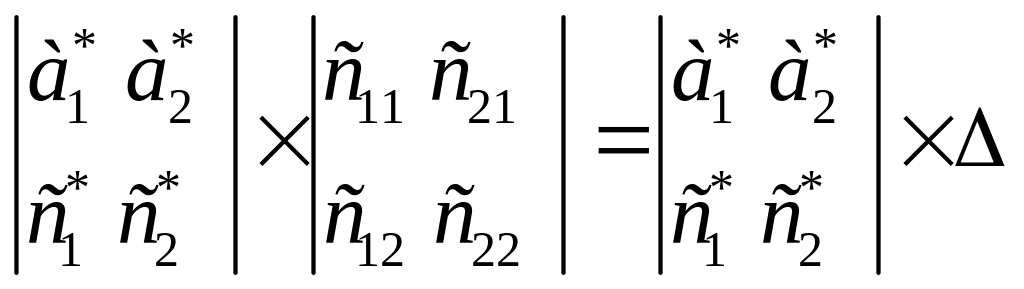

![]() Аналогічно
Аналогічно
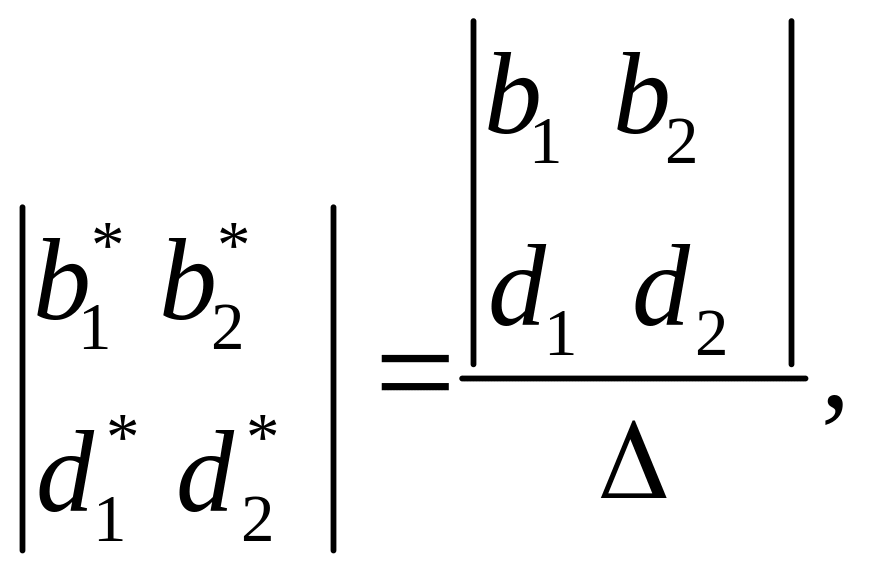

Отже
(АВ,СD)
= 
Складне відношення чотирьох точок не залежить від вибору репера на прямій.
4. Дано : А,В,С,D d, R=(А,В,С) d , D(d1 ,d2)R (АВ,СD)=?
 (АВ,СD)=
(АВ,СD)=![]()
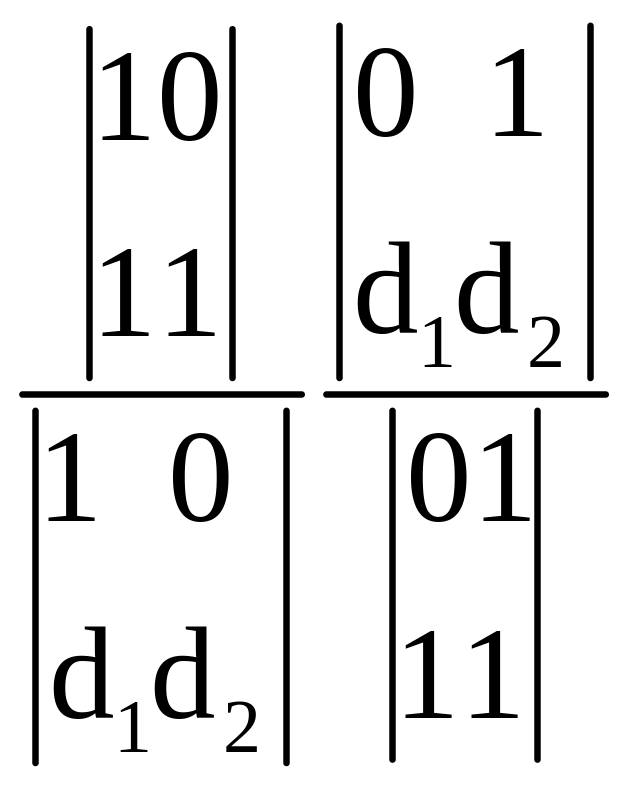 =
=![]()
Складне відношення чотирьох точок прямої, три з яких є точками репера , дорівнює...
5. Чи виражається складне відношення чотирьох точок прямої через прості відношення трьох точок?
Д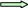 ано:
ано:
![]() d,
d,
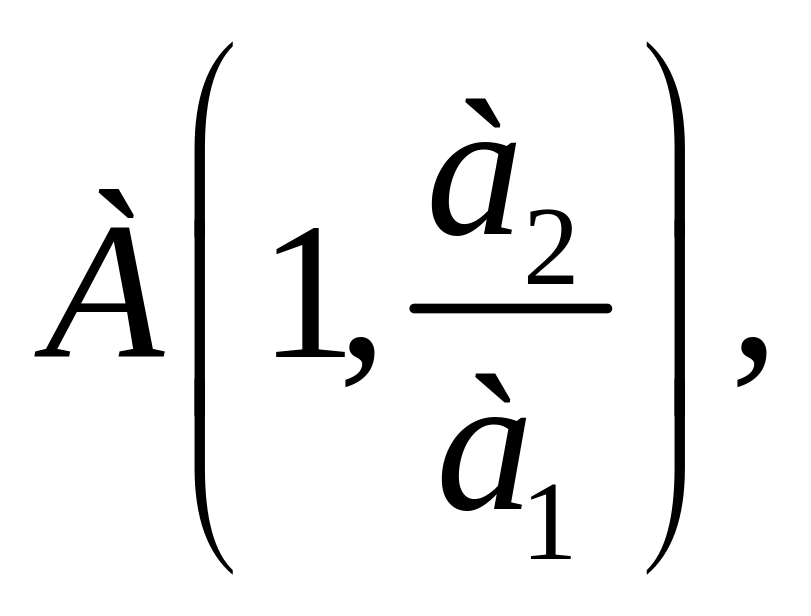
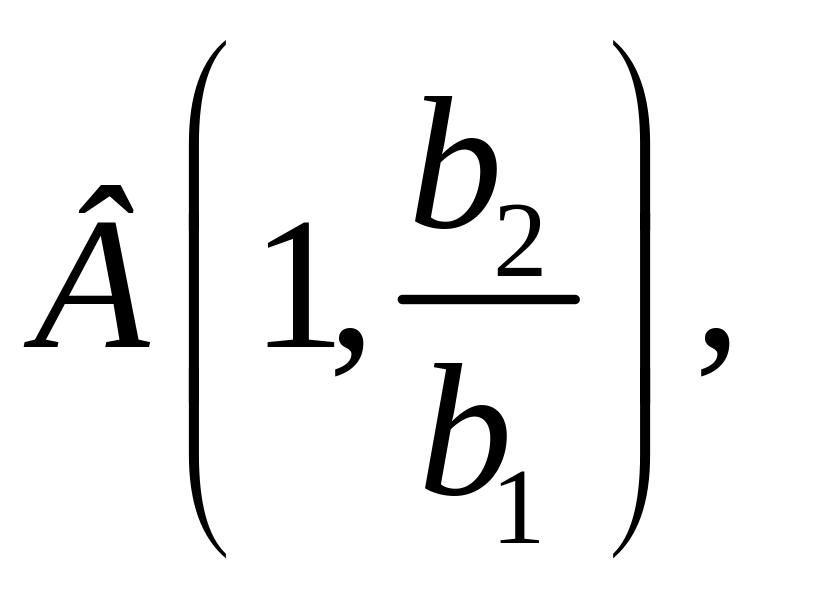


П означимо
означимо
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ---R
---R
![]()
![]()
![]()
![]() ---
---![]()
а ,b, с, d—афінні координати заданих
точок відносно репера R*
( АВ,СD)=
АВ,СD)=
 =
=![]() (1)
(1)
Знайдемо (АВ,С) , (АВ,Д)
( AB,C)=
AB,C)=
![]() ,
За озн.
,
За озн.
![]() ,
,
![]() (AB,C)=
(AB,C)=
![]()
(
AB,D)=
![]() ,
За озн.
,
За озн.
![]() ,
,
![]() (AB,D)=
(AB,D)=
![]()
Тоді
![]() (2)
(2)
З
(1) (2) (АВ,СД)=
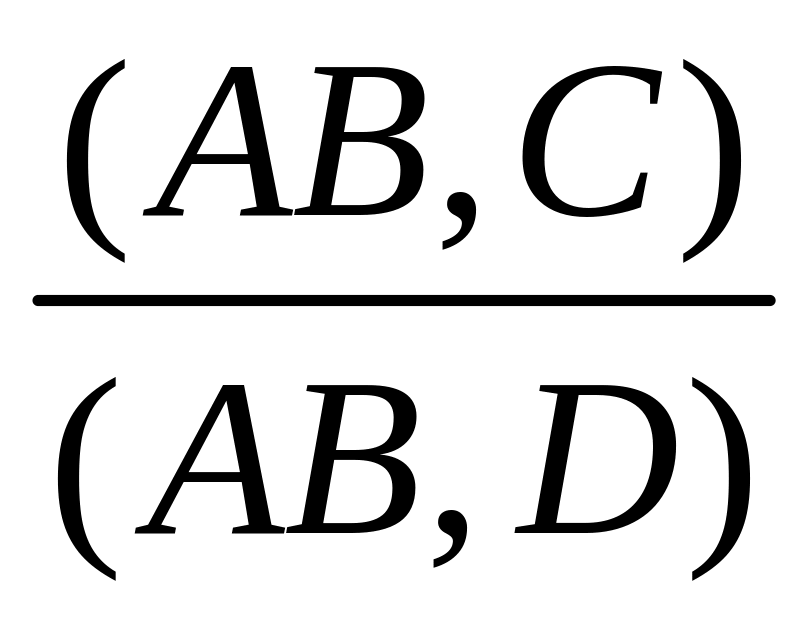
Отже, складне відношення чотирьох точок дорівнює відношенню……….
6.
(АВ,СС)=1
7.
Якщо
(АВ,СD)=(АВ,СМ),
то D=М.
![]()
8. Якщо (АВ,СD)= -1, то складне відношення називається гармонічним.
(АВ,СD)=( СD, АВ )=( ВА,СD)= - 1

Складне відношення чотирьох прямих пучка.
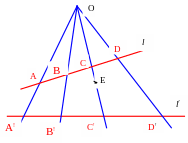
Теорема: Дано : точки А, В, С, D є l,

точки А!, В!, С!, D!- проекції на пряму l!

Дов. (АВ,СD)=( А!В!,С!D! )

Через координати


 R=(
А,В,О,Е)
,
D
єАВ
D(
d1,d2,0)R
,
R=(
А,В,О,Е)
,
D
єАВ
D(
d1,d2,0)R
,
 D(
d1,d2),
R3=(
А,В,C)
D(
d1,d2),
R3=(
А,В,C)
(АВ,СD)= (1)
R!=( А!,В!,О,Е) D! єА!В! D!( d!1,d!2,0) R!,
 D!(
d!1,d!2),
R!3=(
А!,В!,C!)
D!(
d!1,d!2),
R!3=(
А!,В!,C!)
(А!В!,С!D!)=![]() (2)
(2)
Формули перетворення
А !(1,0,а)R
!(1,0,а)R
![]() х1=х1!
х1=х1!
В!(
0,1, b)R
![]() х2=х2!
х2=х2!
О(
0, 0 , 1)R
![]() *
( 1,-а, -b)
х3=ах1!
+в х2!
+( 1-а-в)х3!
*
( 1,-а, -b)
х3=ах1!
+в х2!
+( 1-а-в)х3!


Е(1,1
, 1)R
![]() (1,
1 ,1 ) d1=d1!
(1,
1 ,1 ) d1=d1!
d2=d2! (3)
d3 =
 (1).(2),(3) (АВ,СD)=
(А!В!,С!D!)
(1).(2),(3) (АВ,СD)=
(А!В!,С!D!)
 П(О)+
Т
П(О)+
Т

Складним відношенням чотирьох прямих пучка називається складне відношення чотирьох точок перетину будь-якої прямої з прямими пучка
a b c d
(аb,сd)=(АВ,СD)= (А!В!,С!D!)
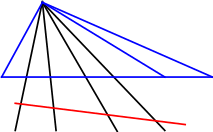
Знаходження складного відношення чотирьох точок прямої через їх координати відносно репера на площині
 A2
P2,
R=( A1,A2,A3,E)
P2
A2
P2,
R=( A1,A2,A3,E)
P2
M (
m1,m2
,
m3
)
(
m1,m2
,
m3
)
N(n1, n2, n3 )
K( k1, k2, k3 ) R
P(p1, p2, p3 )
A1 M2, N2, K2, P2, E2 A3
M N
K P d
M
 ---------M2
M2(m1,m3)
N---------N2
A1A3
N2(n1,n3)
---------M2
M2(m1,m3)
N---------N2
A1A3
N2(n1,n3)
K---------K2 K2(k1,k3) R2=(A1, A3,E2 )
P----------P2 P2(p1,p3)
За теоремою про складне відношення чотирьох прямих пучка
(MN,
KP)=(
M2N2,K2P2)=
Повний 4-вершинник
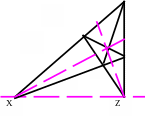
Означення: Повним 4-вершинником називається фігура, яка складається з чотирьох точок проективної площини загального положення та шести прямих, які попарно з’єднують ці точки.
 B
B
![]() - 4-вершинник
- 4-вершинник
![]() і
і![]()
A
![]() і
і
![]()
![]() протилежні
сторони
протилежні
сторони
 Y
Y
![]() і
і
![]()
C
D
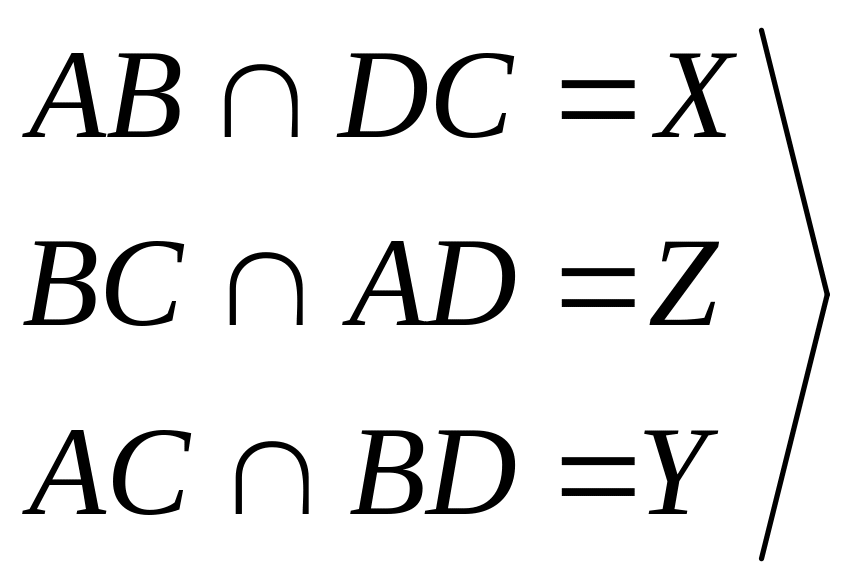 діагональні
точки
діагональні
точки
![]() діагоналі
діагоналі
Теорема: 1) На кожній діагоналі повного 4-вершинника є
четвірка гармонійних точок: дві з яких є діагональними, а дві
інші – це точки перетину цієї діагоналі з протилежними
сторонами, що проходять через третю діагональну точку;
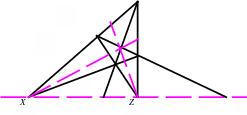 В
В
А - повний 4-вершинник
Y
С
D
M
N
П учок
учок
![]() перетнуто прямими
і
перетнуто прямими
і![]()
![]() Чому?
Чому?
 Пучок
Пучок
![]() перетнуто прямими
і
перетнуто прямими
і
![]() Чому?
Чому?
![]()

![]()
![]()


![]()
якщо отже
![]()
![]() (3)
(3)

![]()
![]()
суперечність умові гармонічна четвірка
2)
з
(1),(3)
![]()
На кожній стороні повного 4-вершинника є четвірка гармонічних точок:
дві з них – вершини, одна діагональна, одна – точка перетину цієї сторони
з діагоналлю, що проходить через дві інші
діагональні точки;
діагоналлю, що проходить через дві інші
діагональні точки;
3)
![]()
Кожна діагональна точка є центром пучка гармонічних прямих, дві з
яких – протилежні сторони, дві інші – діагональні прямі.
