1. Определение

15.1.1. Определённый интеграл как предел интегральной суммы

, где .

15.1.2. Геометрический смысл определённого интеграла – площадь криволи-

b

нейной трапеции.

2. Формула Ньютона – Лейбница вычисления

определённого интеграла

Если непрерывна на отрезке или имеет конечное число конечных разрывов ( I рода ) и , то

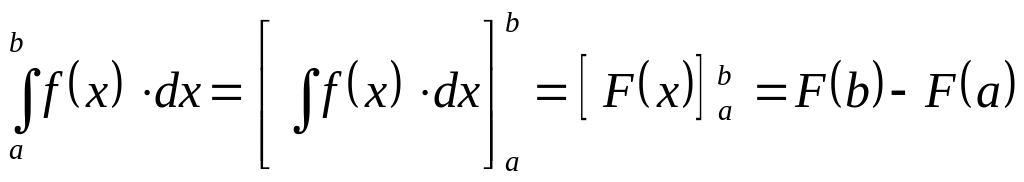
3. Основные свойства определённого

интеграла.

1) = = ,

т.е. результат не зависит от обозначения переменной

интегрирования.

2) .

3) .

4) = + .

5) , где А – пост. .

6) = + .

7) Теорема о среднем: = , где

.

15.4. Основные методы интегрирования

1. Метод замены переменной

Если и , , то

= .

15.4.2. Метод интегрирования по частям

.

15.5.Приближенные вычисления определённых

интегралов

Промежуток интегрирования от а до разбивают на n равных частей и для точек деления вычисляют значения интегрируемой функции . Затем используют одну из следующих формул, полагая :

а) формула прямоугольников: ;

б) формула трапеций: ;

в) формула парабол (Симпсона), n – чётное:

.

15. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

1. Интегралы с бесконечными пределами

а) .

б) .

в) ,

где с – некоторая точка промежутка .

2. Интегралы от разрывных функций

Если непрерывна во всех точках отрезка за исключением точки с, в которой имеет бесконечный разрыв (разрыв II рода), то

= + = + .

15. Некоторые определённые и несобственные интегралы

1.		11.
2.		12.
3.		13.
4.		14.
5.		15.
6.		16.
7.		17.
8.		18.
9.		19.
10.		20.

18. Приложения определенных интегралов

1. Вычисление площадей

1. В прямоугольных координатах

с

2. В полярных координатах

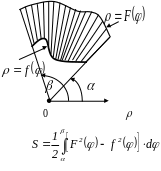
1. Вычисление длин дуг

1. в прямоугольных координатах

Длина дуги гладкой кривой в прямоугольных координатах от точки до точки :

.

18.2.2. в полярных координатах

Длина дуги гладкой кривой в полярных координатах от точки

до точки :

.

18.2.3. КРИВАЯ ЗАДАНА В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ

Длина дуги гладкой кривой , заданной в параметрической

форме, : .

18.3. Вычисление объёмов тел

18.3.1. Объём тела с известным поперечным сечением

2. Объём тела вращения вокруг оси Ох кривой

2. Объём тела вращения вокруг оси Оу кривой