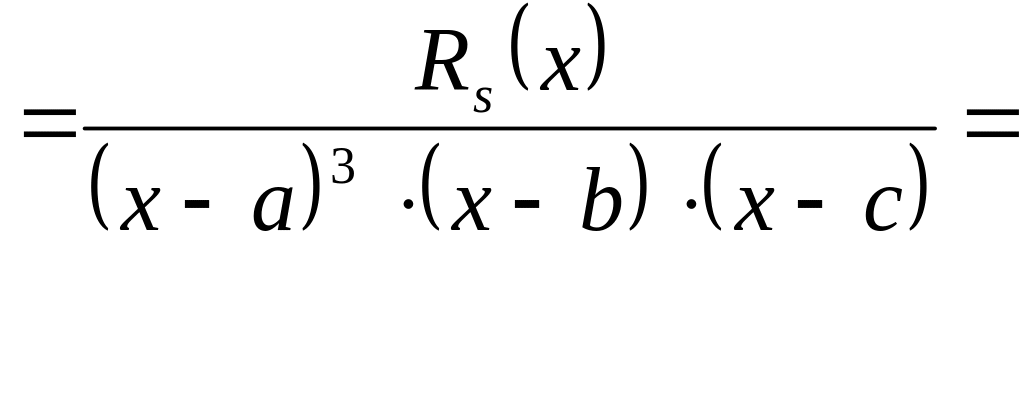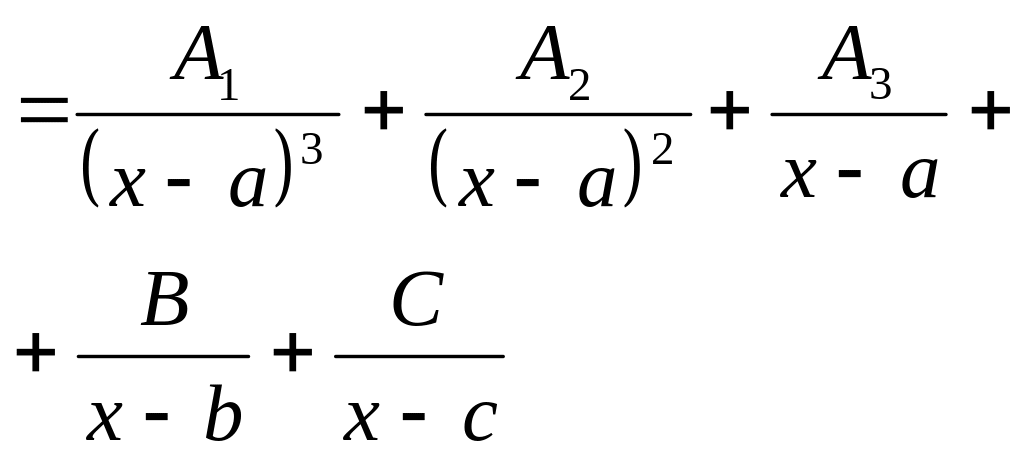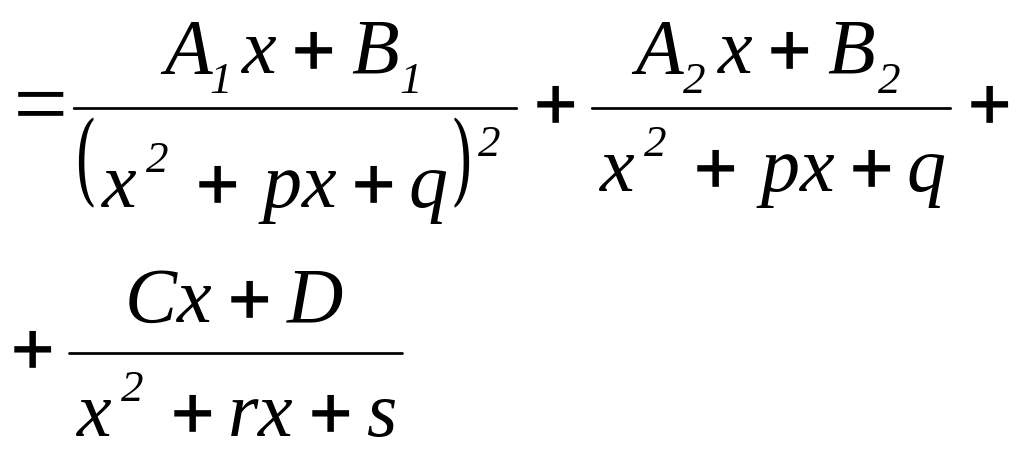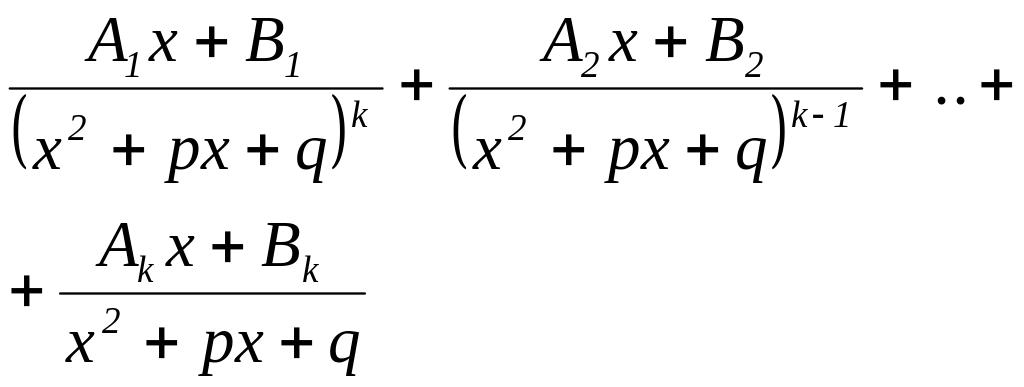2. Интегрирование рациональных дробей

			Вид интеграла		Метод интегрирования
				Если дробь неправильная (т.е. степень числителя больше или равна степени знаменателя: ), то по правилу деления многочлена на многочлен эту дробь всегда можно представить в виде суммы целой рациональной функции и правильной дроби: = .
	=			Целая часть интегрируется непосредственно. Задача свелась к интегрированию правильной дроби. Знаменатель правильной рациональной дроби разлагают на множители первой степени (х – а) (некоторые из них могут повторяться ) и множители второй степени , не имеющих действительных корней (т.е. дискриминант меньше нуля); некоторые из этих множителей также могут повторяться.
	= = + + . . . + .			Если знаменатель правильной рациональной дроби разлагается на множители вида , то каждому множителю соответствует дробь вида , и т.д.
	Пример. =			5) Знаменатель содержит только множители пер вой степени, но некоторые из них повторяются, например: . Тогда каждому множителю вида соответствует следующая сумма дробей: .
	Пример. =			6) Знаменатель правильной дроби содержит множители второй степени . Каждому такому множителю соответствует правильная дробь вида .
	Пример. =			7) Некоторые множители второй степени повторяются, например, . Каждому такому множителю соответствует сумма дробей :

8. Неизвестные коэффициенты разложения А, В, С и т.д. можно находить двумя способами.

Первый способ (метод неопределённых коэффициентов или по другому - метод сравнения коэффициентов). Он состоит в следующем.

• Правильную рациональную дробь разлагают на сумму простейших (как описано выше);

• В правой части этого разложения дроби складывают (приводят к общему знаменателю и т. д.), получают также правильную дробь, после чего знаменатели левой и правой частей (а они одинаковые!) отбрасывают.

• Получают тождественное равенство, в левой части которого стоит многочлен 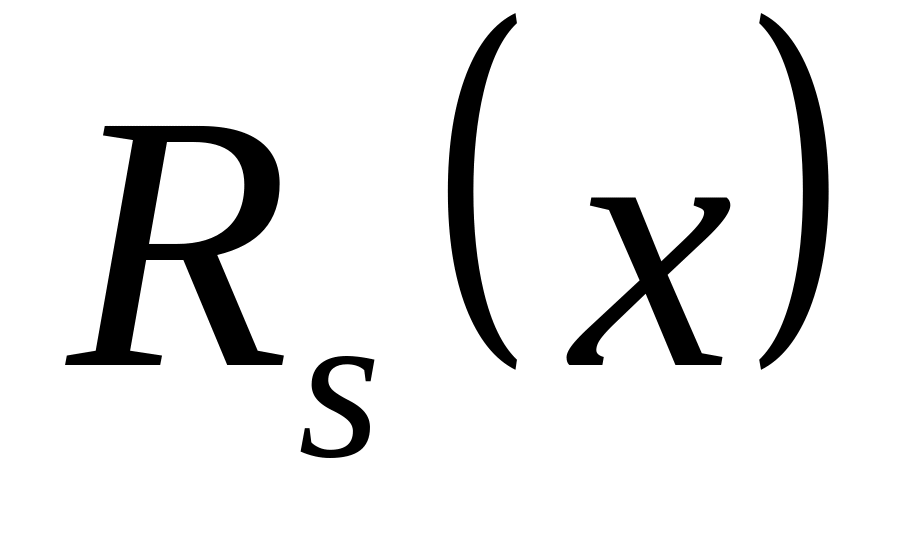с известными коэффициентами, а в правой части стоит многочлен с неизвестными коэффициентами. Приравнивая коэффициенты многочленов при одинаковых степенях х , получим линейную систему из n уравнений c n неизвестными. Решив её , найдём искомые коэффициенты.

Второй способ (метод частных значений).

В полученное тождественное равенство двух многочленов подставляют конкретные числовые значения x . Этим самым вновь получают систему линейных уравнений, из которых и найдутся неизвестные коэффициенты разложения. Для простоты вычислений удобнее придавать переменной x значения, при которых знаменатель правильной дроби обращается в нуль (т.е. значения корней знаменателя ).

Замечание. В практических вычислениях нередко применяют комбинированный прием, т.е. для определения одних коэффициентов применяют первый способ, других – второй.

Пример. Рациональную дробь разложить на сумму простейших.

Решение. Дробь правильная, множитель не имеет действительных корней (т.е. не разлагается на множители), следовательно, разложение имеет вид:

= .

Коэффициенты А.В.С.D,E подлежат определению.

Приводя к общему знаменателю и отбросив его, получаем:

или, после очевидных преобразований,

Приравнивая коэффициенты многочленов, стоящих в левой и правой частях тождества, приходим к системе:

х4 х3

х2 х1

х0

Решив систему, получаем: .

Следовательно, = .
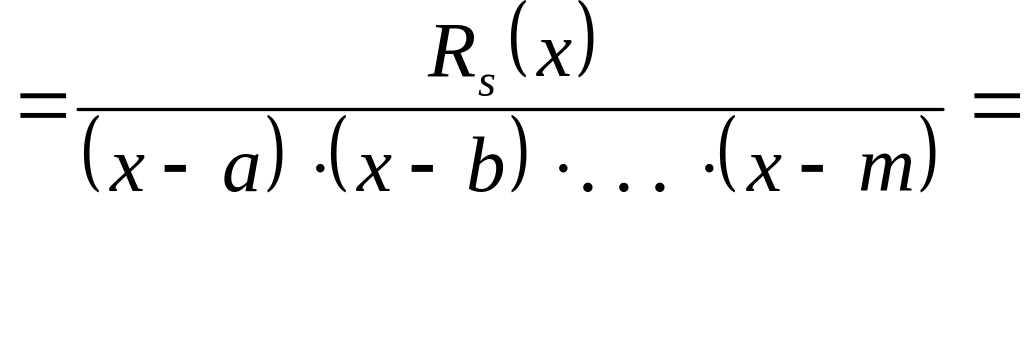