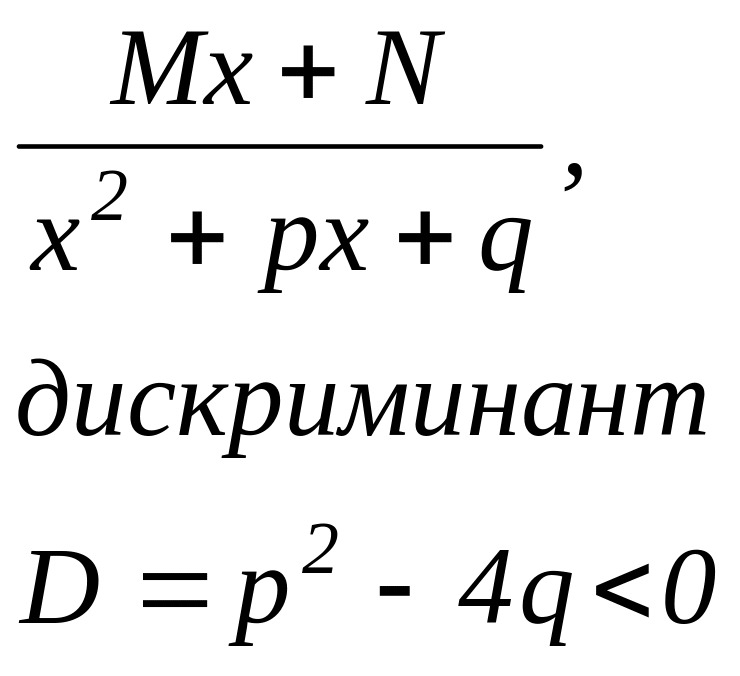- •Обзор используемых приемов интегри-
- •14.5.1. Вычисление интегралов, содержащих квадратный
- •Интегрирование рациональных дробей
- •Интегрирование некоторых иррациональ-
- •14.5.5. Интегрирование квадратичных иррациональностей
- •Интегрирование выражений, содержащих
- •Интегрирование некоторых иррациональностей с помощью тригонометрических подстаново
- •14.6.1. Интегралы от рациональных функций, содержащих
- •Интегралы от рациональных функций, содержащих
- •Интегралы от иррациональных функций, содержащих
- •Интегралы от функций, содержащих
- •Интегралы от некоторых иррациональностей
- •Интегралы, содержащие показательную и логарифмическую функции
- •Интегралы, содержащие тригонометрические функции
- •Определение
- •15.4. Основные методы интегрирования
- •15.4.2. Метод интегрирования по частям
- •Площадь поверхности вращения дуги кривой
- •18.4.1. Кривая задана уравнением
- •18.5. Работа переменной силы
14. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
ОПРЕДЕЛЕНИЕ
Если
![]() ,
то
,
то
![]() .
.
Основные свойства неопределённого
интегр ла
1.
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() ,
где
,
где
![]()
3.
![]()
![]() +
+
![]() .
.
14.3. Основные методы интегрирования
14.3.1 Метод замены переменной ( он же - метод подстановки ):
если
![]() то
то
![]() .
.
Подведение под знак дифференциала
как один из частных приёмов замены переменной:
14.3.3. Метод интегрирования по частям
![]()
Таблица основных интегралов
Таблица производных |
Таблица интегралов |
Обобщенные интегралы |
||||
1º |
|
1.
|
|
|
||
2º |
|
2. |
|
|
||
3º
4º |
|
3.
4. |
|
|
||
5º
6º
7º
8º
|
|
5.
6
7
8
|
|
|
||
9º
10º
11º
12º
|
|
9
10
11
12
|
|
|
||
13º
14º
15º
16º |
|
13
14
15
16 |
|
|
||
17º |
|
17 |
|
|||
18º |
|
18 |
|
|||
Обзор используемых приемов интегри-
рования
14.5.1. Вычисление интегралов, содержащих квадратный
ТРЁХЧЛЕН В ЗНАМЕНАТЕЛЕ
I.
![]() II.
II.
![]()
Частные случаи |
Методы вычисления |
1). В числителе стоит производная квадратного трёхчлен:
|
Эти интегралы вычисляются так:
|
2). В числителе отсутствует х:
а)
б)
|
В обоих случаях в знаменателе выделяют полный квадрат из квадратного трёхчлена. В результате приходят к одному из табличных интегралов: a) Для первого интеграла приходят к виду :
или
б)
Для второго
интеграла (в зависимости от знака а)
интеграл приводится к одному из
табличных интегралов: a>0:
или
a<0 :
|
Общий случай |
|
I.
II.
|
1)
В числителе 1-го интеграла выделяют
производную
квадратного трёхчлена (это можно
сделать, например, делением числителя
на (
где m,n – известные числа, которые появляются после выделения производной, которые являются рассмотренными частными случаями. 2)
После выделения в числителе производной
квадратного трёхчлена (во 2-м интеграле),
приходят к сумме двух интегралов:
которые являются уже рассмотренными частными случаями.
|
|
|||||||||||||||||||||||
|
|
Рекуррентная формула:
|