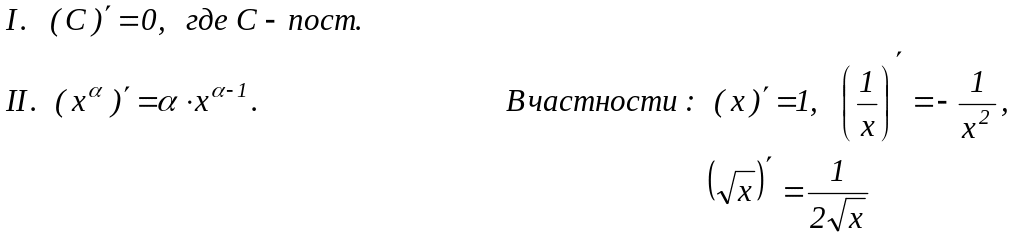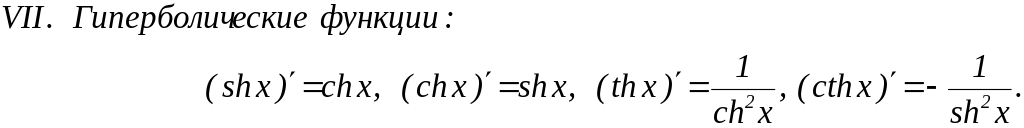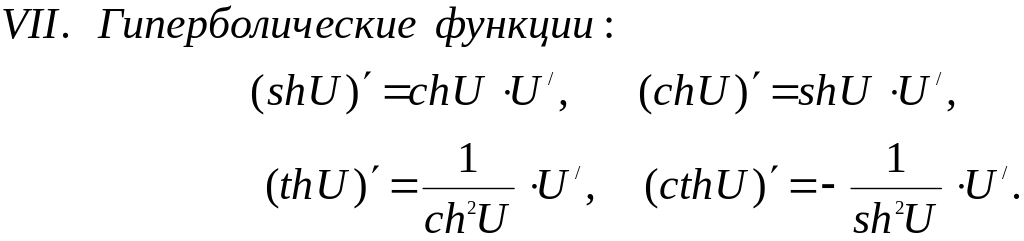11. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ

ОДНОЙ ПЕРЕМЕННОЙ

11.1. Основные теоремы о пределах

1. ;

2. ;

3. ;

4. , где С – пост.;

5. 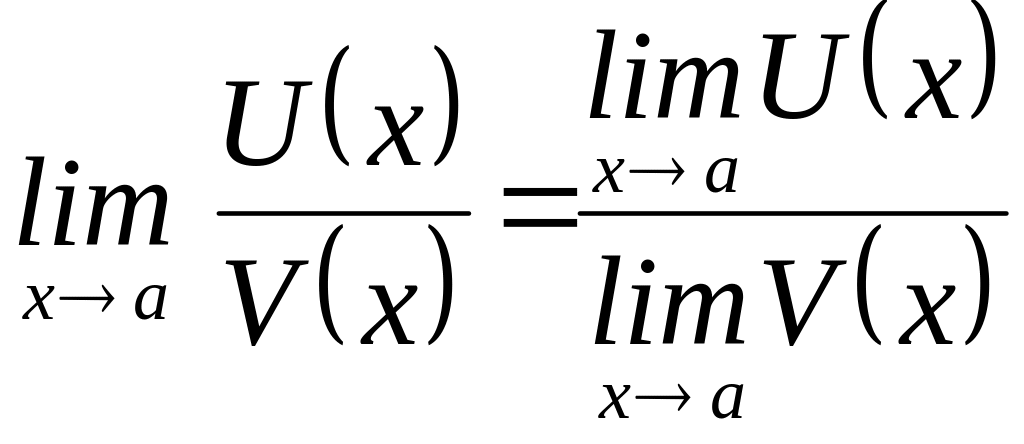, где .

2. Замечательные пределы

Первый: . В общем случае, .

Второй: или

В общем случае, .

11.3. Часто встречающиеся пределы

>0

4. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ

Функция α(x) называется бесконечно малой при , если .

Функция α(x) называется бесконечно большой при , если .

4. Сравнение бесконечно малых

Если , то - бесконечно малая более высокого порядка, чем .

Если (предел конечен и отличен от 0), то функции и называются бесконечно малыми одного и того же порядка.

Если , то и - равносильные (эквивалентные) бесконечно малые: ~ .

г) При эквивалентными являются следующие пары бесконечно малых функций (наиболее употребительные).

11.5.1. ПРИМЕРЫ ЭКВИВАЛЕНТГНЫХ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН

sin(αx)  αx
tg(αx)  αx
arcsin(αx)   αx
arctg(αx)  αx

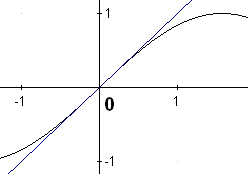
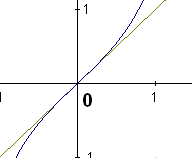
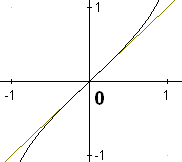
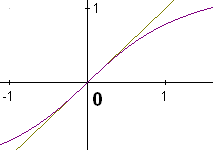
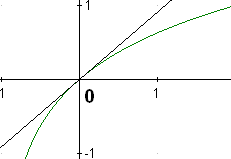
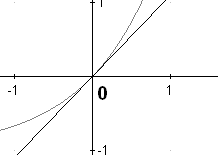
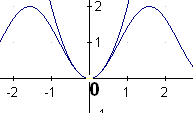
2. ГЕОМЕТРИЧЕСКАЯ ИЛЛЮСТРАЦИЯ ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ

ВЕЛИЧИН

Приближённая формула	Геометрическая интерпретация	Приближённая формула	Геометрическая интерпретация
			,

4. Приближенные формулы

В таблице для каждой приближенной формулы указано, какого числа не должно превосходить абсолютное значение x , чтобы формула давала k точных десятичных знаков.

Формула	k = 2	k = 3	k = 4
	0,07	0,022	0,007
	0,04	0,012	0,004
	0,06	0,022	0,007
	0,19	0,062	0,020
	0,20	0,065	0,021
	0,14	0,047	0,015
	0,04	0,014	0,004
	0,25	0,119	0,055

4. Приращение функции

Приращение функции , соответствующее приращению

аргумента : .

4. Условие непрерывности функции

Условие непрерывности функции :

.

11.9. Основное свойство непрерывной функции

.

11.10. Производная

.

Геометрически - угловой коэффициент касательной к графику функции в точке с абсциссой , т.е. , где - угол наклона касательной к кривой к положительному направлению оси

11. Основные правила дифференцирования

,

,

, где пост. ,

.

Производная сложной функции.

Если где , то

или .

в Предварительное логарифмирование функции часто упрощает вычисление производной:

; дифференцируя, получаем: .

Производная функции, заданной параметрически ,

вычисляется по формуле: .

Вторая производная .

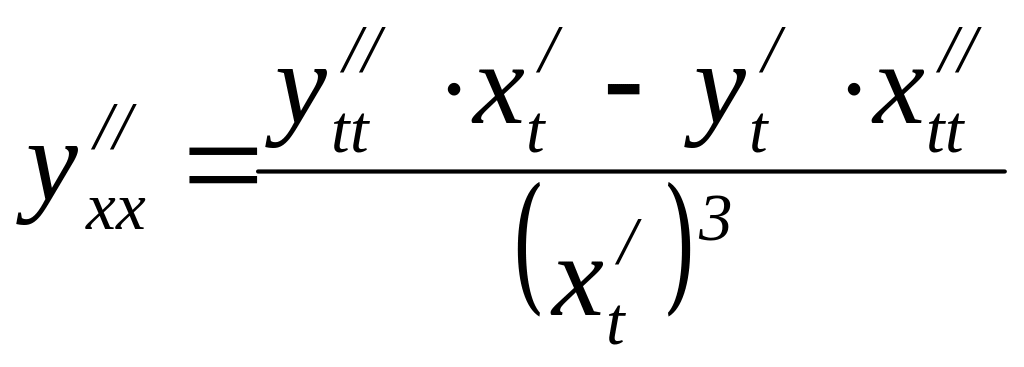Производная обратной функции: , .

11. Таблица производных основных функций

11. Таблица производных сложных функций

( )

.