Контрольные варианты к задаче 4

1. Найти объем треугольной пирамиды, построенной на векторах ,

и .

2. Найти объем треугольной пирамиды с вершинами ,

3. Найти объем треугольной пирамиды с вершинами :

4. Найти объем треугольной пирамиды, вершины которой находятся в точках

и

5. Найти объем треугольной пирамиды с вершинами .

6. Найти объем треугольной пирамиды с вершинами в точках

и

7. Вершины треугольной пирамиды находятся в точках и

8.Найти объем треугольной пирамиды, образованной векторами .

9. Найти объем треугольной пирамиды, образованной векторами

10. Найти объем треугольной пирамиды, образованной векторами .

Задача 5. Даны координаты вершин пирамиды ; .

1. Найти длину вектора .

2. Найти угол между векторами .

3. Найти проекцию вектора на вектор .

4. Найти площадь грани АВС .

5. Найти объем пирамиды ABCD.

Координаты векторов:

1. Длина вектора

2.

3. Проекция вектора на вектор

4.

5.

Контрольные варианты к задаче 5

Даны координаты вершин пирамиды ABCD. Требуется найти:

1) длины векторов

2) угол между векторами

3) проекцию вектора на вектор

4) площадь грани АВС ;

5) объем пирамиды ABCD.

1.		,	,
2.		,	,
3.		,	,
4.		,	,
5.		,	,
6.		,	,
7.		,	,
8.		,	,
9.		,	,
10.		,	,
11.		,	,
12.		,	,
13.		,	,
14.		,	,
15.		,	,
16.		,	,
17.		,	,
18.		,	,
19.		,	,
20.		,	,
21.		,	,
22.		,	,
23.		,	,
24.		,	,
25.		,	,
26.		,	,
27.		,	,
28.		,	,
29.		,	,
30.		,	,

З а д а ч а 6 Общее уравнение плоскости имеет вид: , где - ненулевой вектор, перпендикулярный плоскости (нормальный вектор плоскости).

Уравнение плоскости, проходящей через три данные точки , и определяется равенством

,т.к.

Векторы лежат в одной плоскости, т.е. их смешанное произведение равно нулю . Точка является текущей ,т.е. произвольной точкой плоскости.

Расстояние от точки до плоскости находится по формуле .

Пример 6

Найти расстояние от точки до плоскости, проходящей через точки .

Найдем уравнение плоскости, проходящей через точки :

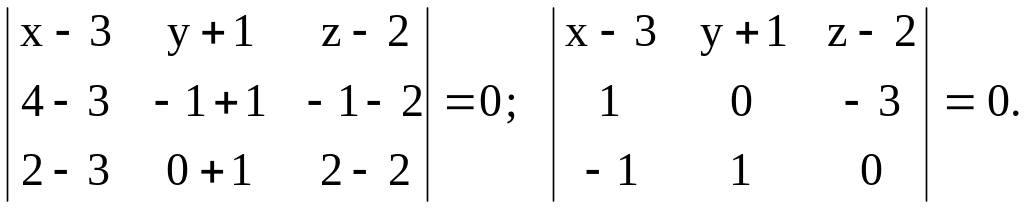
Вычислим определитель, разложив его по первой строке:

Найдем расстояние от точки до плоскости .