2. Теоретическая часть

Необходимое и достаточное условие устойчивости линеаризованных систем формулируется в теоремах А.М.Ляпунова [1,2].

Теорема 1. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво независимо от членов разложения выше первого порядка малости.

Теорема 2. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с положительной вещественной частью, то невозмущенное движение неустойчиво, независимо от членов разложения выше первого порядка малости.

Так как при порядках характеристического уравнения n выше третьего определение корней представляет сложную задачу, то устойчивость реальных систем исследуют с помощью специально разработанных критериев

Критерием устойчивости называются правила, позволяющие исследовать устойчивость системы без непосредственного нахождения корней характеристического уравнения.

Пусть характеристическое уравнение замкнутой системы имеет вид

(2.1)

Тогда формулировки основных критериев устойчивости будут следующие.

Критерий Рауса – алгебраический критерий, позволяющий судить об устойчивости системы по коэффициентам уравнения (2.1).

Формулировка критерия: для устойчивости замкнутой системы необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса были одного с а₀ знака.

Таблица 3

Таблица Рауса

а0	а2	а4	а6	
а1	а3	а5	а7	
C13	C23	C33		
C14	C24	C34		
C1,n+1	0	0	0	0

Таблица Рауса составляется по правилам:

а) в первой строке выписываются все коэффициенты с четными индексами, начиная с а₀, во второй - с нечетными, начиная с а₁, отсутствующие коэффициенты заменяются нулями;

б) коэффициенты третьей строки вычисляются по следующему алгоритму:

С₁₃₌; С₂₃=; С₃₃= и т.д.

в) коэффициенты четвертой строки определяются по двум предыдущим строкам:

С₁₄=;С₂₄=и т.д.

Таблица Рауса имеет (n+1) строку и целое от число столбцов.

Критерий Гурвица. Если характеристическое уравнение системы имеет вид (2.1), то для устойчивости системы необходимо и достаточно, чтобы при а₀>0 главный определитель Гурвица _n и все его диагональные миноры (₁, ₂, …_n-1) были положительными.

Определитель Гурвица _n представляет собой определитель квадратной матрицы n-го порядка, составленной из коэффициентов характеристического уравнения (2.1) так, что по главной диагонали выписываются все коэффициенты, начиная с а₁ и заканчивая а_n; все столбцы заполняются вверх от главной диагонали коэффициентами с возрастающими индексами, а вниз от главной диагонали с убывающими индексами; отсутствующие коэффициенты заменяются нулями.

_n=>0; (2.2)

₁=а₁; ₂=>0;₃=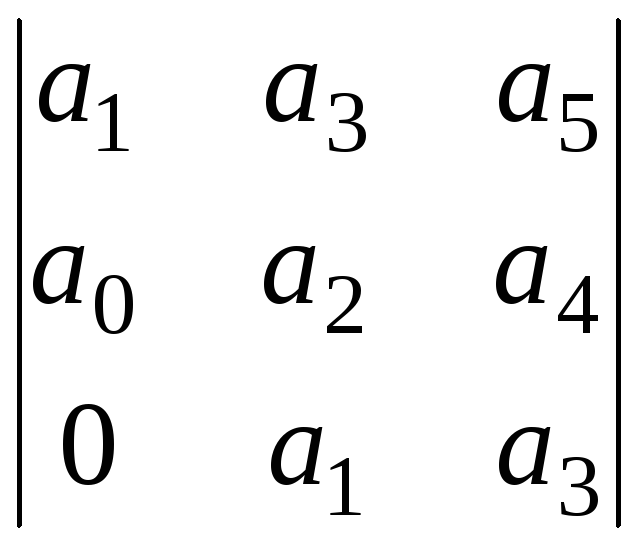>0; ; _n=_n-1а_n.

Критерий Михайлова – частотный критерий, позволяющий судить об устойчивости замкнутой системы по годографу ее характеристического вектора D(j) на комплексной плоскости. Формулировка критерия: для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф характеристического вектора при изменении частоты  от нуля добесконечности, начинаясь на вещественной положительной полуоси, повернулся в положительном направлении (против часовой стрелки) на угол, гдеn - порядок характеристического уравнения, нигде не изменяя своего направления и не обращаясь в нуль, т.е. согласно принципу аргумента

. (2.3)

Критерий Найквиста – частотный критерий, позволяющий судить об устойчивости замкнутой системы с единичной обратной связью по виду амплитудно-фазовой характеристики разомкнутой системы.

Первая формулировка критерия: замкнутая система будет устойчива, если амплитудно-фазовая характеристика устойчивой разомкнутой системы не охватывает точку с координатами , т.е..

Вторая формулировка критерия: если передаточная функция W(s) разомкнутой системы имеет правых корней, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении частоты  от нуля до бесконечности охватывала точку с координатами (-1,) в положительном направлении (против часовой стрелки) раз, т.е..

Формулировка критерия для астатических систем: замкнутая система будет устойчива, если АФХ разомкнутой системы, дополненная дугой бесконечного радиуса до положительной вещественной полуоси, если число правых полюсов  передаточной функции W(s) равно нулю или четное, и до отрицательной вещественной полуоси, если  - нечетное число, при изменении частоты  от нуля до бесконечности охватывает точку с координатами в положительном направлениираз.