
Методичка к системе MATLAB
.pdf31
1
2 >> L=[2 1] L =
21
2.Определим решение уравнения Ляпунова
>> G=dlyap(A, eye(2)) G =
-0.2211 -0.1215 -0.1215 -0.1285
3. Произведем расчет главных миноров
>> det(G(1:1, 1:1)) ans =
-0.2211 >> det(G) ans =
0.0136
По кри тери ю Си львестра реш ени е не я вля ется полож и тельно-опред еленной матри цей, след овательно, си стеманея вля ется аси мптоти чески устойчи вой.
4. А налоги чно мож но опред ели тьсвойство аси мптоти ческой устойчи вости в управля емой си стеме.
>> G=dlyap(A+B*L, eye(2)) G =
-0.2563 |
0.0833 |
|
|
0.0833 |
-0.0498 |
|
|
>> det(G) |
|
|
|
ans = |
|
|
|
0.0058 |
|
|
|
>> det(G(1:1, 1:1)) |
|
|
|
ans = |
|
|
|
-0.2563 |
|
|
|
По кри тери ю Си львестра реш ени е д и скретного уравнени я |
Л япунова не |
||
является |
полож и тельно-опред еленной матри цей, |
след овательно, си стема не |
|
является аси мптоти чески устойчи вой. |
|
|
|
5. При вед ем текст script-ф айла д ля опред елени я |
устойчи вости |
матри цы X на |
|
основеи спользовани я метод аРаусса-Гурви ца. |
|
|
|
%получение коэффициентов характеристического полинома lm= poly(X);
%определение размерности
[L, N] =size(lm);
%создание матрицы с нулевыми значениями g=zeros(N, N);
%заполнение нечетных строк матрицы Гурвица s=0;
for i=1:2:N j=1; j=j+s; r=0;
for r=2:2:N g(i, j)=lm(r); j=j+1;
end s=s+1;
end
%заполнение четных строк матрицы Гурвица s=0;
for i=2:2:N j=1;
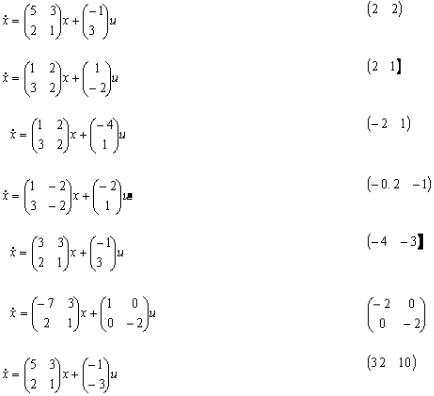
32
j=j+s;
r=0;
for r=1:2:N g(i, j)=lm(r); j=j+1;
end s=s+1;
end
g=g(1:N-1, 1:N-1);
%вычисление главных миноров minor=1;
for i=1:N-1
dd = det(g(1:i, 1:i)); if dd<0
minor=0; end
end
%вывод результатов if minor==0
disp('СИСТЕМА НЕ УСТОЙЧИВА');
else
disp('СИСТЕМА УСТОЙЧИВА');
end |
|
|
|
|
|
|
|
|
|
Результат вы чи слени я показы вает, что си стема |
управлени я не |
я вляется |
|||||||
аси мптоти чески |
устойчи вой. |
Полученны е |
граф и ки |
д и нами ки |
си стемы |
||||
и ллюстри руют |
полученны й |
анали ти чески й |
результат |
о |
неустойчи вости |
||||
си стемы . |
|
|
|
|
|
|
|
|
|
Задани е: в ы полни т ь дейст в и я, при в еденны е в |
при м ере |
для одной и з |
|||||||
си ст ем |
|
|
|
|
|
|
|
|
|
№ № |
У равнени я си стем |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

33
8
9
.
10
.
11
12
13
14
15
16
17
18
.
19
20
3.9. С и нт езопт и м альногоуправ лени яс полнойобрат нойсв язью
Пусть повед ени е мод ели объекта управлени я |
опи сы вается обы кновенны м |
д и ф ф еренци альны м уравнени ем x(t)=f (t, x(t), |
u(t)), гд е х - вектор состояни я |
си стемы , х Rn, Rn - n-мерноеевкли д ово пространство; u - векторуправлени я , и u U Rn, U - некотороезад анноемнож ество д опусти мы х значени й управлени я, t T=[t0, t1] – и нтервал времени ф ункци они ровани я си стемы , моменты начала процессаt0 и окончани я процессаt1 зад аны , f (t, x, u): Т × Rn × U → Rn.

34
Зад анф ункци онал качествауправлени я
гд е f 0(t, x, u), F(x) - зад анны е непреры вно д и ф ф еренци руемы е ф ункци и . Пред полагается , что при управлени и и спользуется и нф ормаци я о текущ ем времени и векторесостояни я х.
При меня емоев каж д ы й моментвремени t Т управлени еи меетви д управлени я c полной свя зью по всем переменны м векторасостояни я (Ри с. 5.).
Ри с.5.
Т ребуется найти такую ф ункци ю u*(t, x) Un, что
 .
.
Ф ункци я u*(t, x) Un назы вается опти мальны м управлени ем сполной обратной cвя зью. Д ля любого начального состояни я x0 и з множ естваRn онапорож д ает соответствующ ую опти мальную пару, т.е. опти мальную траектори ю х*(.) и опти мальноепрограммноеуправлени еu*(.).
Д остаточны м услови ем ми ни мумаф ункци оналая вля ется уравнени еБеллмана д ля непреры вны х д етерми ни рованны х си стем. Е сли сущ ествуют ф ункци я φ(t, x) C1,1, уд овлетворяющ ая уравнени ю Беллманасграни чны м услови ем:
и управлени еu*(t, x) Un, уд овлетворяющ ееуслови ю
то u*(t, x) я вля ется опти мальны м управлени ем сполной обратной свя зью. При этом ми ни мальноезначени еф ункци онала
. |
|
Д ля си нтеза опти мального регуляторов ли нейны х стаци онарны х |
си стем в |
Control System Toolbox и меются ф ункци и реш ени й уравнени й |
Беллмана |
(Т абли ца4.). |
|
Т абли ца4. Ф ункци и Control System Toolbox

|
35 |
|
|
|
|
|
|
Си нтакси с |
|
О пи сани е |
|
|
|
|
|
[K P e] = lqr(A, B, Q, S) |
|
Си нтез непреры вного регулятора |
|
|
|
|
|
[K P e] = lqr(A, B, Q, S, N) |
|
Си нтез непреры вного регулятора |
|
|
|
|
|
[K P e] = dlqr(A, B, Q, R) |
|
Си нтез д и скретного регулятора |
|
|
|
|
|
[K P e] = dlqr(A, B, Q, R, N) |
|
Си нтез д и скретного регулятора |
|
|
|
|
|
[K P e] = lqrd(A, B, Q, R, Ts) |
|
Си нтез д и скретного регулятора |
|
|
|
|
|
[K P e] = lqrd(A, B, Q, R, N, Ts) |
|
Си нтез д и скретного регулятора |
|
|
|
|
K cо |
Ф ункци я lqr вы чи сля ет |
матри |
цу коэф ф и ци ентов регули ровани я |
|
сред неквад рати чны м ф ункци оналом качествабез терми нального члена:
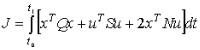 ,
,
при этом вы чи сля ются матри цаP, я вляющ ая ся реш ени ем уравнени я Ри ккати и
собственны езначени я e матри цы (A – BK). |
|
Ф ункци я dlqr вы чи сля ет матри цу коэф ф и ци ентов |
регули ровани я по всем |
переменны м состояни я K д ля д и скретной си стемы |
cо сред неквад рати чны м |
ф ункци оналом качествабез терми нального члена: |
|
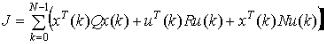 ,
,
при этом вы чи сля ются матри цаP, я вляющ ая ся реш ени ем уравнени я Ри ккати и собственны езначени я e матри цы (A – BK).
Ф ункци я lqrd пред назначенад ля си нтезаопти мального д и скретного регуля тора непреры вной си стемы cо сред неквад рати чны м ф ункци оналом качества:
|
|
. |
|
|
В качестве |
параметра |
в ф ункци ю |
перед ается |
ш аг д и скрети заци и Ts, |
возвращ аются |
значени я |
матри цы K |
д и скретного |
управлени я , матри ца P, |
являющ аяся реш ени ем уравнени я Ри ккати и собственны езначени я e матри цы си стемы управлени я , полученны й в результатед и скрети заци и .
При |
и спользовани и всех команд си нтеза опти мального ли нейного регуля тора |
по |
всем переменны м состояни я на и сход ны е д анны е наклад ы ваются |
след ующ и еограни чени я :
- си стема, опред еляемая матри цами (A, B), д олж набы тьстаби ли зи руема; - д олж ны вы полня ться неравенстваS> 0, Q – NR–1NT>0,
- параматри ц(Q – NR–1NT, A – BR–1BT) нед олж наи метьнаблюд аемы емод ы ссобственны ми значени я ми над ействи тельной оси .
При мер 12. М од ели ровани е си стемы управлени я и си нтез опти мального регуля тора.
Н и ж епри вод и тся текстscript-ф айла:
% Параметры си стемы
A=[1 0; -2 1];
B=[1 0; 1 0]';
36
%Параметров кри тери я качествауправлени я
Q=[1/2 0;0 1/2]; R=[1/2 0; 0 1/2];
%В ремя регули ровани я
T=10;
%В ели чи наш ага
SS=0.5;
%К оли чество ш агов
N=T/SS
%В ы чи слени епараметров регулятора
[k p e]= dlqr(A, B, Q, R) x = zeros(2, N);
u= zeros(2, N-1);
%Н ачальны еуслови я
x(1,1)=2;
x(2,1)=1;
% Построени еграф и ков д и нами ки си стемы for i=1:N-1,
u(:, i)= - k*x(:, i);,
x(:, i+1)=A*x(:, i)+B*u(:, i); end
x1= x(1,:); x2= x(2,:);
t = 0:SS:T-SS; subplot(4, 1, 1); plot(t, x1, 'b'); subplot(4, 1, 2); plot(t, x2, 'g'); subplot(4, 1, 3);
plot(SS:SS:T-SS, u(1, :), 'y'); subplot(4, 1, 4); plot(SS:SS:T-SS, u(2, :), 'r');
Результаты вы чи слени я след ующ и е: значени я параметров опти мального регуля тора–
k = |
|
0.8229 |
-0.1771 |
0.8229 |
-0.1771 |
p = |
|
3.7343 |
-1.4114 |
-1.4114 |
1.1614 |
e = |
|
0.1771 |
+ 0.1771i |
0.1771 |
- 0.1771i |
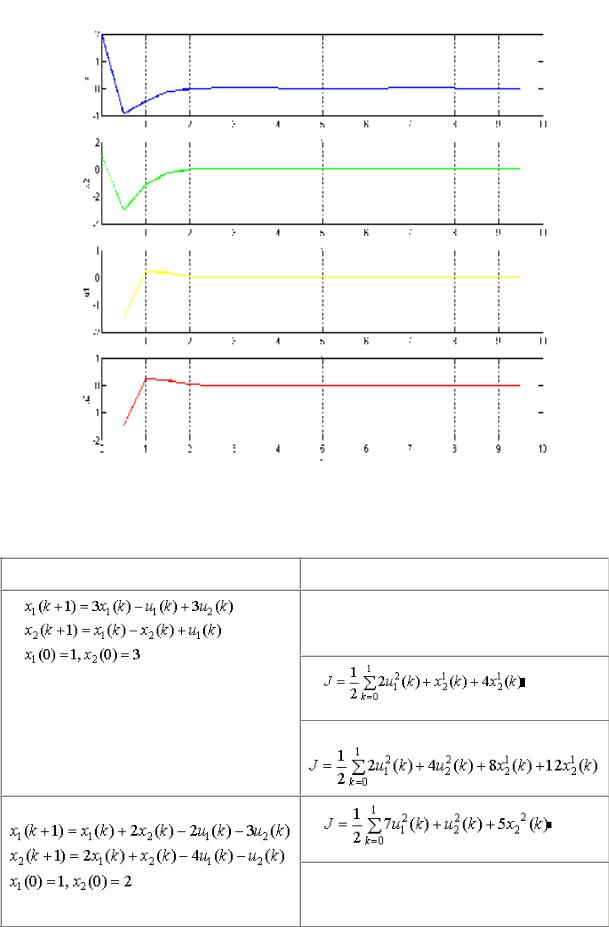
граф и ки д и нами ки си стемы – Ри с. 6.
37
Ри с. 6.
Задани е: осущест в и т ь м одели ров ани е заданной си ст ем ы управ лени я с учет ом в ы бранногоф ункци онала.
М од ельси стемы |
Ф ункци онал качествауправлени я |
1. 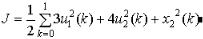
1.
2.
3.
2.
1.
2. 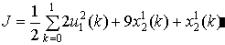

38
3. 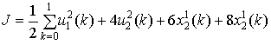
1. 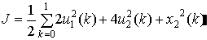
3.
2.
3. 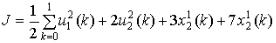
1. 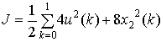
4.
2.
3. 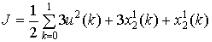
4. SIMULINK
ПрограммаSimulink явля ется при лож ени ем кпакету MATLAB, реали зующ и м при нци п ви зуального программи ровани я . При этом пользователю не нуж но д осконально и зучатья зы кпрограмми ровани я и чи сленны еметод ы математи ки ,
д остаточно общ и х знани й, требующ и хся |
при |
работе на компьютере и , |
|||
естественно, знани й той пред метной области , в которой онработает. |
|
||||
Д ля работы с Simulink не требуется |
знатьсам MATLAB и остальны е его |
||||
при лож ени я , од нако д оступкф ункци я м MATLAB и его и нструментам остается |
|||||
откры ты м, что позволя ет и спользоватьи х |
при |
мод ели ровани и в Simulink. |
|||
Пользователь мож ет созд авать свои |
собственны е би бли отечны е блоки , |
||||
и зменя тьсущ ествующ и е, |
а такж е составля тьновы е би бли отеки |
блоков. В |
|||
процессе мод ели ровани я |
мож но след и ть за |
прои сход ящ и ми |
в си стеме |
||
процессами спомощ ью специ альны х блоков, азатем пред ставля тьрезультаты мод ели ровани я в ви д еграф и ков и ли табли ц.
4.1.Началоработ ы
Д ля того чтобы начатьработатьсSimulink, мож но воспользоваться од ни м и з трех способов:
- в команд ном окнеMATLAB вы полни тькоманд у Simulink;
- воспользоваться кнопкой бы строго д оступа  (Simulink) на панели и нструментов;
(Simulink) на панели и нструментов;

|
39 |
- вы братьопци ю Open… |
в меню File и откры тьф айл мод ели (mdl - |
ф айл) в том случае, |
если мод ель уж е бы ла ранее созд ана и |
отлаж ена. |
|
В результате эти х д ействи й на экране буд ет отображ ено О кно обозревателя разд елов би бли отеки Simulink. Под робно состав окна обозревателя опи сан в
[2,3].
4.2. С оздани е м одели
Созд атьновы й ф айл мод ели мож но спомощ ью кнопки бы строго д оступа и ли опци и File/New/Model главного меню. О кно мод ели показанонаРи с. 7.
и ли опци и File/New/Model главного меню. О кно мод ели показанонаРи с. 7.
Ри с7.
Т еперьмож но при ступатькмод ели ровани ю. Д ля этого след ует располож и ть нуж ны е блоки в окне мод ели : откры тьсоответствующ и й разд ел би бли отеки , затем, указав курсором натребуемы й блоки наж ав налевую кнопку “мы ш и ”, “перетащ и ть” блокв созд анноеокно, уд ерж и вая кнопку наж атой, послеэтого след уетсоед и ни тьблоки . Размеры блоков и и х размещ ени ев окнеи зменяются станд артны м д ля ви зуальны х сред способом. Параметры блоков, установленны е“по умолчани ю”, меняются в окнеред акти ровани я параметров, д ля чего след уетуказатькурсором наи зображ ени еблокаи д важ д ы щ елкнуть левой клави ш ей “мы ш и ”. При зад ани и чи сленны х параметров след уети метьв ви д у, что в качествед есяти чного разд ели теля д олж наи спользоваться точка, а незапя тая . Послевнесени я и зменени й нуж но закры тьокно кнопкой OK.
После установки на схеме всех требуемы х блоков элементы схемы соед и ня ются . Д ля этого указатькурсором на“вы ход ” блока, азатем наж атьи , неотпуская левую клави ш у “мы ш и ”, провести ли ни ю квход у д ругого блокаи отпусти тьклави ш у. В случаеправи льного соед и нени я и зображ ени естрелки на вход еблокаи зменяетцвет. Д ля созд ани я точки разветвлени я в соед и ни тельной
ли ни и нуж но под вести курсор к пред полагаемому узлу |
и , наж ав правую |
клави ш у “мы ш и ”, протянутьли ни ю. Д ля уд алени я ли ни и |
требуется вы брать |
ли ни ю (каки блок), азатем наж атьклави ш у Delete. |
|
Послесоставлени я схемы онасохраняется в ви д еф айланад и скеспомощ ью опци и File/Save As... в главном меню мод ели . В д альнейш ем загрузкамод ели
40
осущ ествля ется спомощ ью опци и File/Open... в окнеобозревателя би бли отеки и ли и з основного окнаMATLAB.
4.3. Т екст ов ы е надпи си
Д ля |
повы ш ени я нагляд ности мод ели уд обно и спользоватьтекстовы енад пи си . |
|
Д ля |
созд ани я над пи си нуж но указать мы ш ью место над пи си |
и д важ д ы |
щ елкнутьлевой клави ш ей мы ш и . А налоги чно мож но и змени тьи |
под пи си к |
|
блокам мод ели . След уети метьв ви д у, что возмож ны труд ности при попы тке и спользовани я ки ри лли чески х ш ри ф тов (отображ ени енад пи сей в нечи таемом ви д е, обрезани е над пи сей, сообщ ени я об ош и бках, а такж е невозмож ность откры тьмод ельпослееесохранени я ).
4.4.И зм енени е парам ет ров расчет а
Перед вы полнени ем расчетов требуется зад ать параметры расчета, что осущ ествля ется спомощ ью пунктаменю Simulation/Parameters.
О кно настройки параметров расчетаи меет4 вклад ки :
∙Solver (Расчет) — установкапараметров расчетамод ели .
∙ |
Workspace |
I/O (В вод /вы вод |
д анны х в рабочую область) — установка |
параметров обменад анны ми срабочей областью MATLAB. |
|||
∙ |
Diagnostics |
(Д и агности ка) |
— вы бор параметров д и агности ческого |
реж и ма. |
|
|
|
∙Advanced (Д ополни тельно) — установкад ополни тельны х параметров.
У становка параметров расчета мод ели вы полня ется с помощ ью элементов управлени я , размещ енны х на вклад ке Solver. Более под робная и нф ормаци я о вклад ках при вед енав [2].
4.5. Вы полнени е расчет а
Запускрасчетавы полняется спомощ ью вы борапунктаменю Simulation/Start.
и ли и нструмента напанели и нструментов. Процессрасчетамож но заверш и ть
напанели и нструментов. Процессрасчетамож но заверш и ть
д осрочно, вы брав пунктменю Simulation/Stop и ли и нструмент . Расчеттакж е мож ноостанови ть(Simulation/Pause) и затем прод олж и ть(Simulation/Continue).
. Расчеттакж е мож ноостанови ть(Simulation/Pause) и затем прод олж и ть(Simulation/Continue).
4.6. Зав ерш ени е работ ы
Д ля заверш ени я работы необход и мо сохрани тьмод ельв ф айле, закры тьокно мод ели , окно обозревателя би бли отек, атакж еосновноеокно пакетаMATLAB. Задани е: и спользоватьSimulink д ля мод ели ровани я од ной и з при вед енны х вы ш еси стем.
Ли т ерат ура
1.Потемки н В .Г. Справочни кпо MATLAB: справ. пособи е / В .Г.Потемки н.-
М .:Д И А Л О Г-М И Ф И , 1998. -318с.
