Методичка к системе MATLAB
.pdf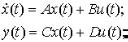
21
В Control System Toolbox и меется ти п д анны х, опред еляющ и х д и нами ческую си стему в пространстве состояни й. Си нтакси с команд ы , созд ающ и й непреры вную LTI (Linear Time Invariant)-си стему в ви д е ss-объекта c од ни м
вход ом и од ни м вы ход ом SS(A, B, C, D). |
|
|
||
В |
эту ф ункци ю в качестве параметров перед аются матри цы уравнени й |
|||
состояни й и вы ход ов ви д а |
|
|
||
М |
атри цу д и нами ки D буд ем счи татьв д анном случаенулевой. |
|||
Д ля вы полнени я работы могутпри меняться команд ы (Т абли ца3.). |
||||
|
|
|
Т абли ца3. |
|
|
|
Си нтакси с |
О пи сани е |
|
|
|
|
|
|
|
|
ctrb(LTI-объект>) |
Ф орми ровани ематри цы управляемости |
|
|
|
ctrb(A, B) |
|
|
|
|
|
|
|
|
|
obsv(<LTI-объект>) |
Ф орми ровани ематри цы наблюд аемости |
|
|
|
obsv(A, C) |
|
|
|
|
|
|
|
|
|
parallel(<LTI1>,<LTI2>) |
Параллельноесоед и нени е |
|
|
|
|
|
|
|
|
series(<LTI1>,<LTI2>) |
Послед овательноесоед и нени е |
|
|
|
|
|
|
|
|
feedback(<LTI1>,<LTI2>) |
Соед и нени еобратной свя зью |
|
|
|
|
|
|
|
|
append( <LTI1>, … , <LTIN>) |
О бъед и нени еси стем |
|
|
|
|
|
|
|
|
connect(<sys>,<Con>,<in>,<out>) |
У становлени есвя зей в соед и нени и |
|
|
|
|
|
|
Д ля получени я результатов вы чи слени я матри ц, результи рующ ей си стемы , по структурной схеме, воспользуемся послед ни ми д вумя команд ами .
Ф ункци я append созд аетобъектsys, пред ставляющ и й собой объед и нени евсех под си стем. При этом первы й вход ной си гнал первой си стемы станови тся вход ом номер1, второй вход ной си гнал первой си стемы – номер2 и т.д ., д алее и д утвход ы второй си стемы и т.д .; аналоги чно опред еля ются и вы ход ы .
В ф ункци и |
connect |
– параметр <Con> |
опред еля ет матри цу свя зей по |
|||||
структурной |
схеме. М |
атри ца ф орми руется |
по след ующ ему прави лу: |
каж д ая |
||||
строка пред ставля ет собой од и н вход |
си стемы |
sys, первы й элемент – номер |
||||||
вход а (в соответстви и |
с поряд ком в команд е append), затем и д ут номера |
|||||||
вы ход ов, |
которы е сумми руются |
и |
под аются |
на рассматри ваемы й |
вход . |
|||
Параметры |
<in>, <out> – строки |
и з номеров вход ов и вы ход ов соед и нени я , |
||||||
являющ и еся внеш ни ми .
Н апри мер, д ля послед овательного соед и нени я д вух си стем:
sys1= ss(A1, B1, C1, D1) sys2= ss(A2, B2, C2, D2) sys=append (sys1, sys2)
sysc=connect(sys, [2 1], [1], [2])
В этом случаенавход второй си стемы (общ и й вход номер2), поступаетвы ход первой (общ и й вы ход номер 1); вход первой си стемы (номер од и н) и вы ход второй си стемы (номерд ва) я вля ются внеш ни ми .
22
При мер10. Д аны три ли нейны естаци онарны еси стемы :
1. |
; 2. |
; 3. |
; |
и и меется структурная схемасоед и нени я си стем:
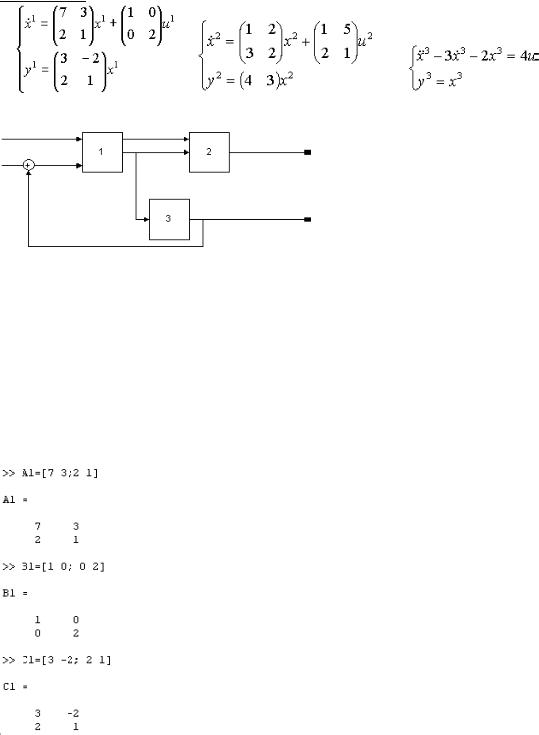
1. При вед ем си стему 3 кд ругому ви д у, д ля чего введ ем переменны е
;
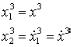и , под ставля я и х в и сход ны еуравнени я , получи м –
; 
; 
.
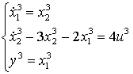2. Созд ад и м матри цы первой си стемы –
Созд авая аналоги чно матри цы д вух д руги х си стем, созд ад и м ss-объекты :
23
24
3. И сслед уем наблюд аемостьи управля емостькаж д ой си стемы , д ля чего построи м соответствующ и ематри цы и посчи таем и х ранги –
В и д но, что во всех случая х ранги матри ц управляемости и наблюд аемости совпад аютсразмерностями пространствасостояни й.
4. Получи м си стему, опред еляемую соед и нени ем.
|
25 |
|
|
Д ля корректного и спользовани я |
ф ункци и |
connect |
введ ем д ополни тельную |
си стему, перед аточная ф ункци я |
которой |
равна |
1. Э кви валентная схема |
при вед енанаРи с. 4. |
|
|
|
Ри с. 4.
>>s4 = tf(1) Transfer function: 1
>>sys=append(s1,s2,s3,s4);
>>Q=[2 -4 5; 3 1 0; 4 2 0; 5 2 0];
>>in=[1 5];
>>out=[3 4];
>>s_com=connect(sys,Q, in,out);
О бращ ая ськд анны м объекта, мож но получи тьматри цы А , В , С:
>>A=s_com.A;
>>B=s_com.B;
>>C=s_com.C;
4. В ы чи сли м ранги матри цнаблюд аемости и управля емости и тоговой си стемы :
>>rank(ctrb(A,B)) ans =
6
>>rank(obsv(A,C)) ans =
6
Результаты показы вают, что д анная си стемауправля емаи наблюд аема. Задани е: и спользоватьод и ни з след ующ и х вари антов
№ № |
У равнени я си стем |
|
|
Схема |
|
|
|
|
|
1 |
|
|
|
1 |
|
1. |
2. |
3. |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
1. |
2. |
3. |
|
|
|
|
|
|
3 |
|
|
|
3 |
|
1. |
2. |
3. |
|
|
|
|
|
|
|
|
|
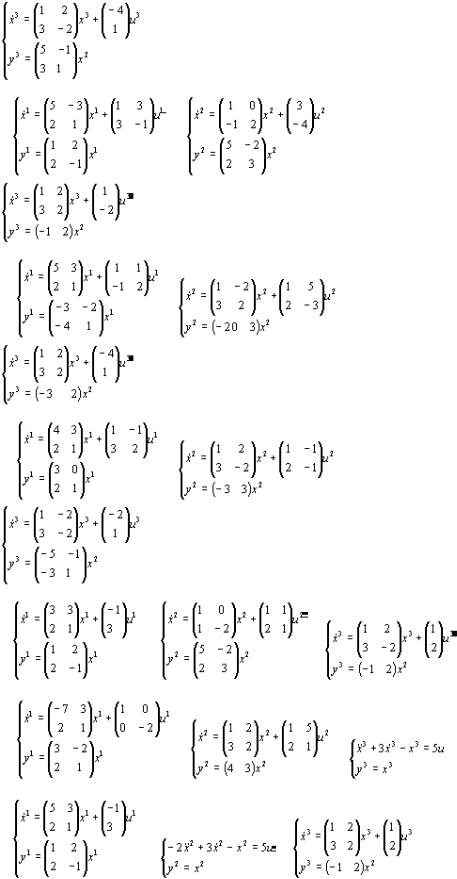
26 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
1. |
2. |
3. |
|
|
|
|
|
|
5 |
|
|
|
2 |
|
1. |
2. |
3. |
|
|
|
|
|
|
6 |
|
|
|
3 |
|
1. |
2. |
3. |
|
|
|
|
|
|
7 |
|
|
|
1 |
|
1. |
2. |
3. |
|
|
|
|
|
|
8 |
|
|
|
2 |
|
1. |
2. |
3. |
|
|
|
|
|
|
9 |
|
|
|
5 |
|
1. |
2. |
3. |
|
|
|
|
|
|
|
|
|
|
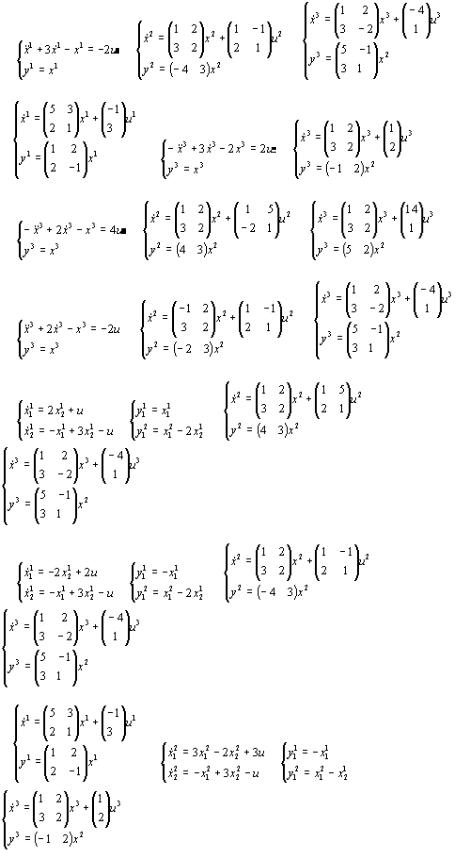
27 |
|
|
|
|
|
|
|
10 |
|
|
|
|
6 |
|
1. |
2. |
|
3. |
|
|
|
|
|
|
|
11 |
|
|
|
|
5 |
|
1. |
2. |
|
3. |
|
|
|
|
|
|
|
12 |
|
|
|
|
7 |
|
1. |
2. |
|
3. |
|
|
|
|
|
|
|
13 |
|
|
|
|
6 |
|
1. |
2. |
|
3. |
|
|
|
|
|
|
|
14 |
|
|
|
|
8 |
|
1. |
|
2. |
3. |
|
|
|
|
|
|
|
15 |
|
|
|
|
8 |
|
1. |
|
2. |
3. |
|
|
|
|
|
|
|
16 |
|
|
|
|
9 |
|
1. |
2. |
|
3. |
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
17 |
|
|
|
10 |
|
1. |
2. |
3. |
|
|
|
|
|
|
18 |
|
|
|
8 |
|
1. |
2. |
|
|
|
3. |
|
|
|
|
|
|
|
|
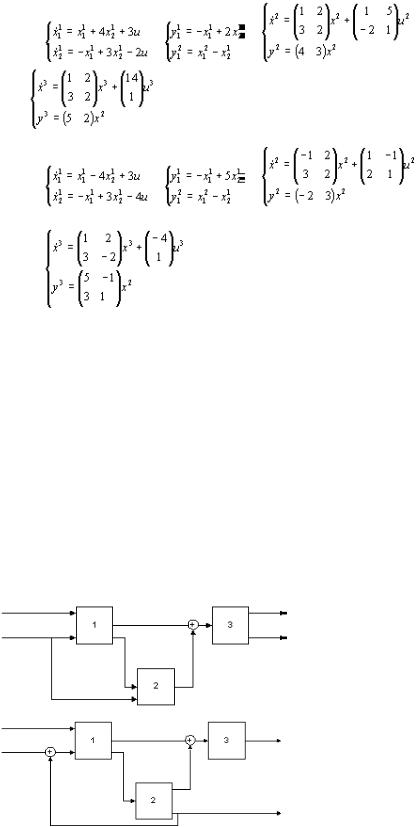
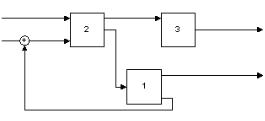
Структурны есхемы квари антам
1. 
2. 
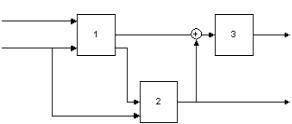
3.
4.
29
5.
6.
7.
8.
9.
10. |
|
|
3.8. Уст ойчи в ост ьли нейны х си ст ем |
|
|
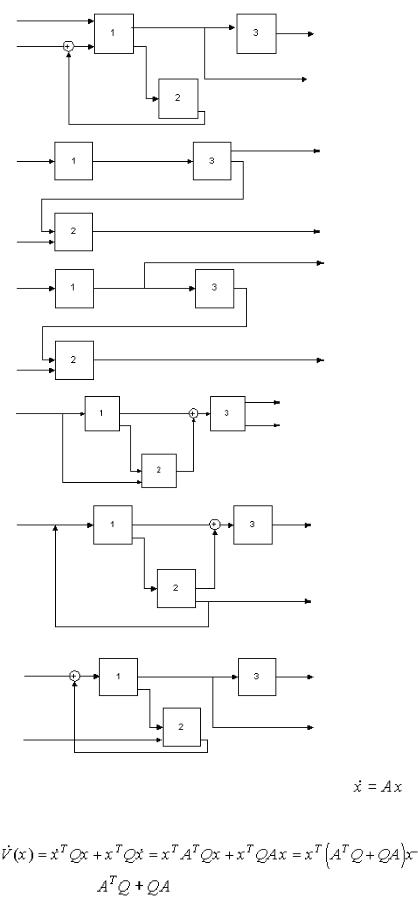
Рассмотри м ли нейную стаци онарную си стему |
. |
|
Д опусти м, что |
уд алось найти ф ункци ю |
Л япунова: V(x)=xTQx, гд е Q – |
си мметри чная и полож и тельная опред еленная матри ца. Т огд а |
||
О бозначи м |
= – С (*), тогд а, поскольку С полож и тельно опред елена, |
|
си стемааси мптоти чески устойчи вав целом. Болеетого, т.к.
30 |
|
|
, |
матри ца |
С |
си мметри чна.
Н а практи ке целесообразно реш атьобратную зад ачу. В ы би рают какую-ли бо полож и тельно опред еленную полож и тельную матри цу, напри мер C = I. Т огд а мож но получи тьQ. Е сли квад рати чная ф ормаQ оказы вается неопред еленной
(знакопеременной), то по теореме |
Л япунова |
о |
неустойчи вости начало |
||||
коорд и нат неустойчи во. Е сли |
Q полож и тельно |
опред елена, то поскольку |
|||||
си стемали нейнаи стаци онарна, |
начало коорд и натаси мптоти чески устойчи во в |
||||||
целом. |
О боснованность такого анали за зави си т от того, опред еля ет ли |
||||||
уравнени е (*) |
од нозначно матри цу |
Q, |
если |
|
зад ана си мметри чная и |
||
полож и тельная С . |
|
|
|
|
|
||
Справед ли вы след ующ и еутверж д ени я : |
|
|
|
|
|||
Е сли n |
собственны х значени й |
λ1, … |
, λn |
матри цы |
A таковы , что λi+λj <0 |
||
( |
), то и з уравнени я (*) при зад анной матри цеСматри цаQ опред еляется |
||||||
од нозначно. (Д остаточноеуслови еустойчи вости матри цы А ). |
|||||||
Е сли матри цаА |
устойчи ваи матри цаС полож и тельно опред елена, то матри ца |
||||||
Q такж е полож и тельно опред елена. |
(Н еобход и мое услови е устойчи вости |
||||||
матри цы А ). |
|
|
|
|
|
|
|
Си стемааси мптоти чески устойчи вав том и только том случае, если реш ени еГ,
являющ ееся (n×n)-матри цей, уравнени я Л япунова |
Зд есь H – прои звольная |
|||||||||
является |
полож и тельно-опред еленной |
матри цей. |
||||||||
полож и тельно-опред еленная си мметри чная |
матри ца. |
Д ля |
опред еленности |
|||||||
матри цу H мож но полож и тьед и ни чной. |
|
|
|
|
|
|
||||
Д ля установлени я полож и тельной опред еленности |
си мметри чной матри цы |
Г |
||||||||
мож но воспользоваться |
кри тери ем Си львестра: |
i > 0 |
д ля |
, гд е |
i – |
|||||
ми норы |
i-го |
поряд ка |
матри цы |
Г. |
Д ля |
опред елени я |
аси мптоти ческой |
|||
устойчи вости |
ли нейны х |
си стем |
мож но воспользоваться кри тери ем Раусса- |
|||||||
Гурви ца. |
Согласно этому кри тери ю, си стема я вляется |
устойчи вой, если все |
||||||||
ми норы матри цы Гурви цабы ли полож и тельны . А си мптоти ческая устойчи вость опред еляется аналоги чно, только вместо матри цы A берется матри цаA+BL.
При мер11.
Пусть |
зад ана си стема |
управлени я , |
опи сы ваемая |
конечно-разностны ми |
уравнени я ми в пространствесостоя ни й |
|
|
||
x(k+1) |
= A(k) x(k) + B(k) |
u(k), ( |
), |
и и звестна |
матри ца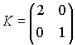
, опред еляющ ая законуправлени я u = Kx,.
1. Зад ад и м матри цы , опред еляющ и еси стему:
>> A=[1 2; -3 4] A =
1 |
2 |
-3 |
4 |
>> B= [1 2]' B =