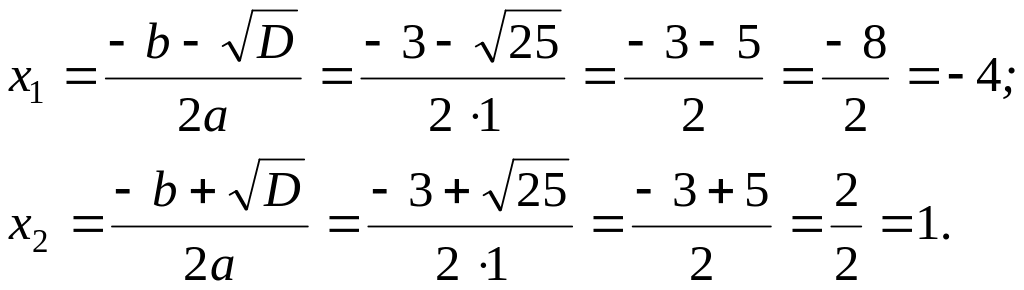Вычислить предел функции:

не противоречит основному правилу: «на нуль делить нельзя»

Получили неопределённость типа , для её устранения разложим и числитель, и знаменатель дроби на множители, затем сократим дробь и вычислим полученный предел:

при решении этого примера будем использовать:

• ФСУ – разность квадратов: а²-b²=(а-b)·(а+b);

• разложение квадратного трёхчлена на множители: ах²+bх+с=·а(х-х₁)·(х-х₂), где х₁; х₂ – его корни.

х²-1=х²-1²=(х-1)(х+1); х²+3х-4=1·(х-(-4))·(х-1)=(х+4)·(х-1).

х²+3х-4=0 (а=1; b=3; с=-4);

D=b²-4ac=3²-4·1·(-4)=9+16=25

Получили неопределённость типа , для её устранения разложим и числитель, и знаменатель дроби на множители, затем сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения разложим знаменатель дроби на множители, умножим и числитель, и знаменатель дроби на выражение сопряжённое числителю, затем преобразуем, сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения умножим и числитель, и знаменатель дроби на произведение выражений сопряжённых числителю и знаменателю, затем преобразуем, сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения умножим и числитель, и знаменатель дроби на выражение сопряжённое знаменателю, разложим числитель на множители, затем преобразуем, сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения умножим и числитель, и знаменатель дроби на произведение выражений сопряжённых числителю и знаменателю, затем преобразуем, сократим дробь и вычислим полученный предел:

Получили неопределённость типа , для её устранения подведём пример к первому замечательному пределу:

Получили неопределённость типа , для её устранения подведём пример к первому замечательному пределу: