Многочлены. Разложение рациональной функции на элементарные дроби.__________

Виды многочленов:

Многочлен n-ой степени	А0хn+А1хn-1+…+Аn-2х2+Аn-1х+Аn	Примеры
Многочлен четвёртой степени	Ах4+Вх3+Сх2+Dх+E	-х4-2х3+3х2+8, где А=-1; В=-2; С=3; D=0; E=8;
Многочлен третьей степени	Ах3+Вх2+Сх+D	2х3-х2+4х, где А=2; В=-1; С=4; D=0;
Многочлен второй степени	Ах2+Вх+С	-х2+4х-3, где А=-1; В=4; С=-3;
Многочлен первой степени	Ах+В	х+8, где А=1; В=8;
Многочлен нулевой степени	А	1, где А=1.

Разложение многочлена на множители.

1. Разложите многочлен на множители:

f(x)=х3+2х2-5х-6, выпишем делители свободного члена: 1; 2; 3; 6. x=1  не корень, так как f(1)=1+2-5-6=80 x=1 корень, так как f(1)=1+2+5-6=0 х3+2х25х6 | x+1 x3+x2 x2+x6 x25х6 x2+x 6x6 6x6 0 f(x)=х3+2х25х6=(x+1)(x2+x6)= =(x+1)(x2)(x+3) x2+x6=0 D=25 f(x)=(x+1)(x2)(x+3)	f(x)=х3+3х24х12, выпишем делители свободного члена: х3+3х24х12 | x f(x)= х3+3х24х12= f(x)=(x2)(x+2)(x+3)
f(x)=х3+2х2+5х+4, выпишем делители свободного члена: 1; 2. x=1 корень, так как f(1)=1+25+4=0 f(x)=	f(x)=х33х2+5х6,

Простейшие дроби часто называют элементарными дробями.

Различают следующие виды простейших дробей:

I
II
III	, где D=p2-4q<0
IV	, где D=p2-4q<0

Называют их соответственно дробями первого, второго, третьего и четвертого типов. Для чего вообще дробь раскладывать на простейшие?

Приведём математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов.

Вспомним, как складывались дроби с разными знаменателями:

Привести дроби к общему знаменателю	Разложить дробь на сумму простейших

Теорема 1: Если рациональная функция имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q(x) представим в виде:

Q(x)=А(x-)^r(x-)^s…(x²+px+q)^t(x²+ux+v)^l,

то эту функцию можно представить единственным образом в виде:

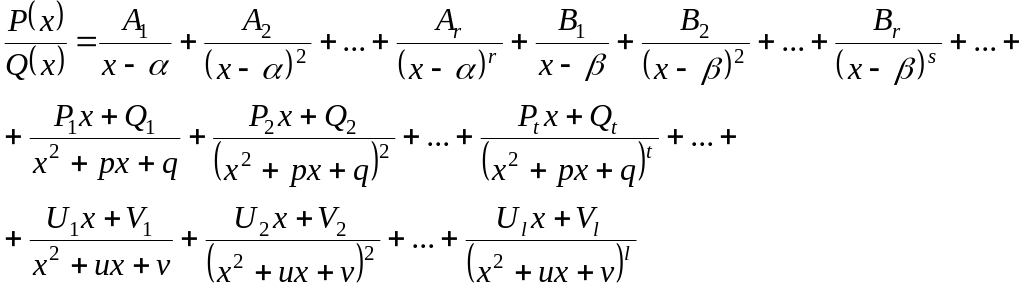
Данное разложение называется разложением рациональной функции на элементарные дроби.

Теорема 2: Если рациональная функция имеет степень многочлена в числителе не меньше степени многочлена в знаменателе, то выполнив деление получим:

,

где W(x) — некоторый многочлен, а R(x) — многочлен степени меньше, чем Q(x).