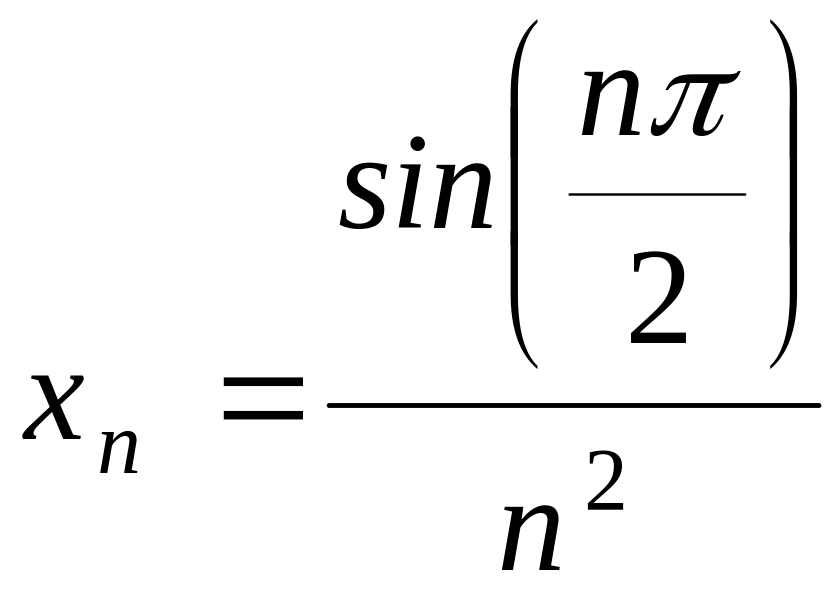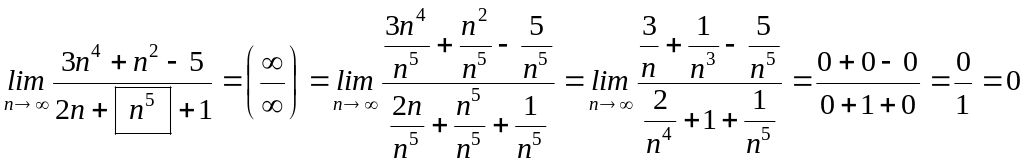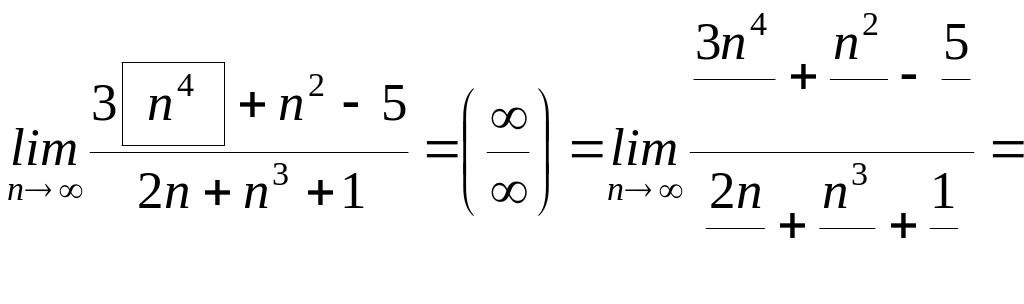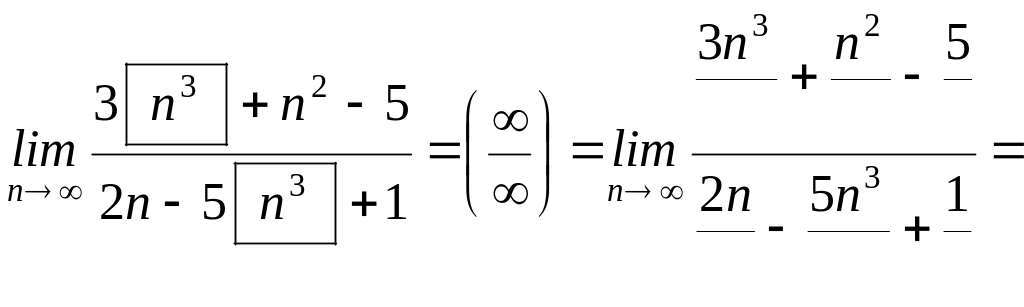- •Дана формула общего элемента последовательности. Указать пять первых её элементов:
- •Зная несколько первых элементов последовательности, написать формулу общего элемента последовательностей:
- •Последовательность заданна реккурентно. Найти х90, х238 и х 885:
- •Вычислить предел последовательности:
- •Вычислить предел последовательности (устно), в случае получения бесконечного предела уточнить знак:
- •Вычислить предел последовательности:
- •Вычислить предел последовательности (устно), в случае получения бесконечного предела уточнить знак:
- •Числовые последовательности. Теория.
- •Предел числовой последовательности. Практика.
Предел числовой последовательности.__________________________________________
Опр.: Если каждому члену n из натурального ряда чисел поставлено в соответствие вещественное число хn, то множество вещественных чисел х1, х2, …, хn – называется числовой последовательностью {хn}.
Числа х1, х2, …, хn – элементы (члены) последовательности; хn - общий элемент (член) последовательности; число n - номер последовательности.
Опр.: Формула, задающая хn – называется формулой общего элемента (члена) последовательности.
Дана формула общего элемента последовательности. Указать пять первых её элементов:
1)
|
2)
|
3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная несколько первых элементов последовательности, написать формулу общего элемента последовательностей:
№ |
Элементы |
Формула |
|||
1 |
|
|
|||
2 |
|
|
|||
3 |
|
|
|||
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|||
Последовательность заданна реккурентно. Найти х90, х238 и х 885:
|
||
|
n=5 |
|
|
n=6 |
|
n=1 |
n=7 |
|
n=2 |
n=8 |
|
n=3 |
n=9 |
|
n=4 |
n=10 |
|
х90= |
х238= |
х885= |
Вычислить предел последовательности:
|
|
|
|
|
|
|
|
|
Получили
неопределённость типа
|
||
|
Получили неопределённость типа , для её устранения разделим и числитель, и знаменатель дроби на старшую её степень, то есть на ____, а затем сократим дробь и вычислим полученный предел:
Это не противоречит основному правилу: «на нуль делить нельзя», так как в знаменателе не «точный нуль», а близкое к нему значение, то есть «приближённый нуль». |
||
|
Получили
неопределённость типа
|
||
При вычислении предела последовательности в случае раскрытия неопределённости типа , можно руководствоваться следующим правилом: Определяем старшую степень выражения и если «старшая степень находится»:
|
||
Вычислить предел последовательности (устно), в случае получения бесконечного предела уточнить знак:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|