2. Алгоритм решения задач

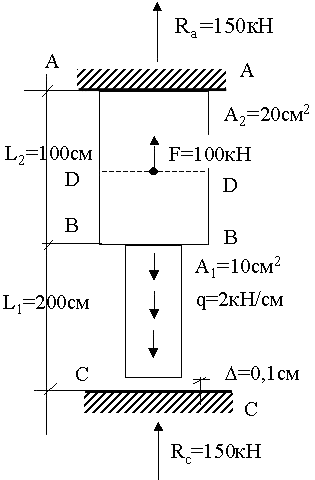
Задача 1. Статически определимый ступенчатый стержень под действием внешних сосредоточенных сил.

1. Определяют (если необходимо) реакцию в жесткой заделке.

2. Стержень разбивают на участки.

3. Используя метод сечений, определяют продольные усилия на каждом участке стержня.

4. По найденным значениям усилий строят эпюру силы N.

5. Зная продольные усилия и площади поперечного сечения участков стержня, определяют напряжения на них.

6. По значениям напряжений на участках стержня строят эпюру напряжений.

7. Определяют деформации отдельных участков стержня.

8. По значениям деформаций вычисляют перемещения граничных сечений участков стержня, начиная расчет от заделки.

9. По значениям перемещений граничных сечений участков стержня строят эпюру перемещений.

Задача 2. Статически неопределимый стержень под действием внешних сосредоточенных сил.

1. Определяют степень статической неопределимости системы. Если стержень с зазором, следует убедиться, что конструкция действительно статически неопределима. Для этого необходимо мысленно отбросить заделку со стороны зазора и вычислить полную деформацию конструкции, считая ее статически определимой. Если полученная деформация растяжения больше величины зазора, получаем статически неопределимую систему. В противном случае, если после нагружения зазор не перекрывается, задачу необходимо решать как статически определимую.

2. Определяют каждую из опорных реакций, составляя для этого дополнительные уравнения совместности деформаций.

3. Проводят проверку правильности определения опорных реакций.

4. Далее последовательность выполнения задачи сводится к задаче 1, начиная с п. 2.

Задача 3. Статически неопределимый ступенчатый стержень (с зазором или без него) под влиянием изменения температуры.

1. Если стержень с зазором, необходимо убедиться, что конструкция является статически неопределимой.

1. Определяют степень статической неопределимости стержневой системы.

2. Определяют одну из опорных реакций (они равны по величине), составляя дополнительное уравнение совместности деформаций.

3. Используя метод сечений, определяют продольное усилие в стержне и строят эпюру силы N.

4. Разбивают стержень на участки.

5. Определяют напряжения на участках стержня, и строят эпюру.

7. Определяют деформации отдельных участков стержня.

8. По значениям деформаций вычисляют перемещения граничных участков стержня, начиная расчет от заделки без зазора.

9. По значениям перемещений граничных сечений строят эпюру перемещений.

Задача 4. Статически неопределимый ступенчатый стержень с зазором под действием сосредоточенных и распределенных внешних сил.

Последовательность выполнения задачи аналогична выполнению задачи 2.

3. Примеры решения типовых задач

Требуется построить эпюры продольных сил, напряжений и перемещений.

З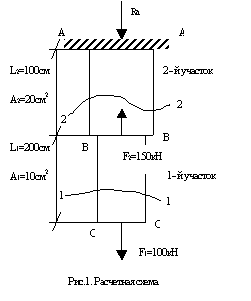 адача 1. Исходные данные: дан двухступенчатый стержень (рис. 1);

Е= 2·10⁴ кН/см².

Решение. 1. Определяем реакцию в заделке А:

;

– R_а + F₂ – F₁ = 0;

R_а = F₂ – F₁ =

= 150 – 100 = 50 кН.

2. Разбиваем стержень на участки – границами являются концевые сечения, места изменения поперечного сечения и точки приложения сил.

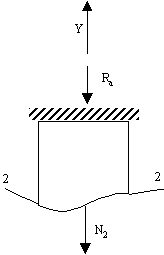
Имеем два участка (рис. 2).

3. Определяем продольные усилия на участках:

участок 1 – 1

N₁ – F₁ = 0;

N₁ = F₁ = 100 кН;

участок 2 – 2

– R_а – N₂ = 0;

N₂ = – R_а = – 50 кН.

4. По значениям продольных усилий N строим эпюру (рис.3,а).

5. Определяем напряжения по участкам:

₁ = N₁ / А₁ = 100 / 10 = 10 кН/см²;

₂ = N₂ / А₂ = – 50 / 20 = – 2,5 кН/см²;

6. По значениям напряжений строим эпюру напряжений  (рис.3,б).

Участок 1 – 1

Участок 2 – 2

Рис. 2. Расчетные схемы к определению продольных сил методом сечений.

7. Определяем деформации отдельных участков стержня:

ℓ₁ = N₁ℓ₁ / ЕА₁ = 100·200 / 2·10⁴·10 = 0,1 см;

ℓ₂ = N₂ℓ₂ / ЕА₂ = – 50·100 / 2·10⁴·20 = – 0,0125 см.

8. Вычисляем перемещения граничных сечений участков стержня:

S_вв = ℓ₂ = – 0,0125 см;

S_сс = S_вв + ℓ₁ = – 0,0125 + 0,1 = 0,0875 см.

9. По значениям перемещений строим эпюру S (рис.3,в).

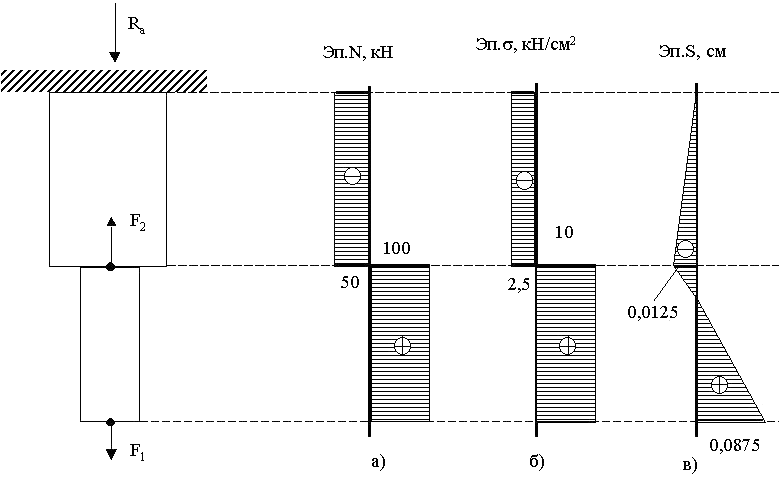
Рис. 3. Построение эпюр продольных сил N, напряжений  и перемещений S.

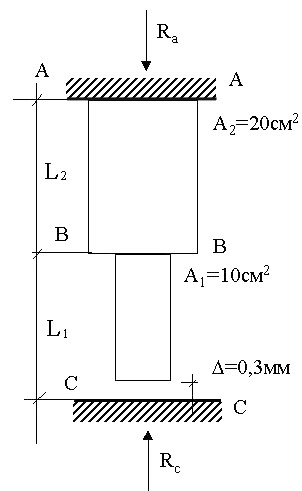
Задача 2. Исходные данные: дан двухступенчатый стержень (рис. 4); А₁ = 10 см²; А₂ = 20 см²; L₁ = 200 см; L₂ = 100 см; F₁ = 100 кН; F₂ = 50 кН; Е = 2·10⁴ кН/см².

Рис. 4. Расчетная схема стержня к задаче 2.

Решение. 1. Определяем степень статической неопределимости системы:

ΣF(у) = 0;

– R_а + F₂ – F₁ – R_с = 0;

Получили одно уравнение статики, неизвестных – две. Следовательно, система один раз статически неопределима.

2. Обратимся к изучению де-формации системы (рис. 5). Мысленно отбросим нижнюю заделку. Предположим, что конструкция под действием внешних сил укоротилась на ℓ^F.

С другой стороны, реакция R_с должна вернуть сечение с-с в первоначальное положение, т.е. получили дополнительное уравнение совместности деформаций: |ℓ^Rc| = |ℓ^F|, или

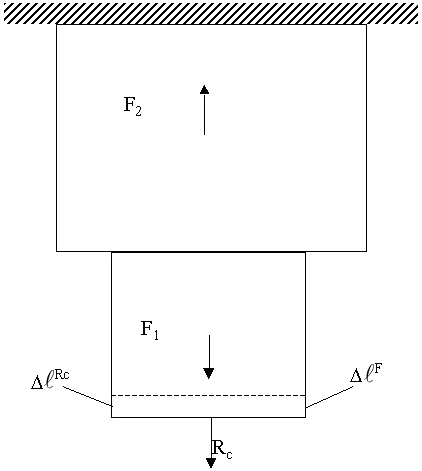
Рис. 5. Схема к анализу деформации системы.

ℓ^Rc + ℓ^F = 0.

Запишем это уравнение, используя закон Гука:

ℓ^Rс = R_cL₁ / ЕА₁ + R_cL₂ / ЕА₂:

С учетом того, что А₂ = 2А₁ и L₁ = 2L₂ получим:

ℓ^F = F₁L₁ / 2EA₁ + F₁L₂ / EA₁ – F₂L₂ / 2EA₂;

R_cL₁ / EА₁ + R_cL₁ / EА₂ + F₁L₁ / 2EА₂ + F₁L₂ / 2EА₂ – F₂L₂ / 2EА₂ = 0;

R_c(2L₂ / A₁ + L₂ / A₁) = F₂L₂ / 4A₁ – F₁2L₂ / 2A₁ – F₁L₂ / 2A₁;

2,5R_c = 0,25F₂ – 1,5F₁;

R_c = (0,25F₂ – 1,5F₁) / 2,5 = (0,25·150 – 1,5·100) / 2,5 = – 45 кН;

R_c = – 45 кН.

На расчетной схеме изменяем направление реакции R_c (рис. 4).

Рассуждая аналогично, найдем реакцию в верхней заделке R_a.

Уравнение совместности деформаций

ℓ^Ra + ℓ^F = 0;

ℓ^Ra = – R_аL₂ / EA₂ – R_aL₁ / EA₁;

ℓ^F = – F₁L₁ / 2EA₁ + F₂L₂ / 2EA₂ + F₂L₁ / EA₁;

С учетом, что А₂ = 2А₁ и L₁ = 2L₂ имеем:

– R_аL₂ / E2A₁ – R_а2L₂ / EA₁ – F₁2L₂ / 2EA₁ + F₂L₂ / 2E2A₁ + F₂2L₂ / EA₁=0;

–R_а (1/2 + 2) = F₁ – F₂ / 4 – 2F₂;

R_а = (2,25F₂ – F₁) / 2,5 = (2,25·150 – 100) / 2,5 = 95 кН;

R_а = 95 кН.

3. Проводим проверку правильности определения реакций. Составляем сумму проекций всех сил на ось У:

F(у) = 0; – R_а + F₂ – F₁ + R_с = 0;

– 95 + 150 – 100 + 45 = 0;

– 195 + 195 = 0;

Реакции определены верно.

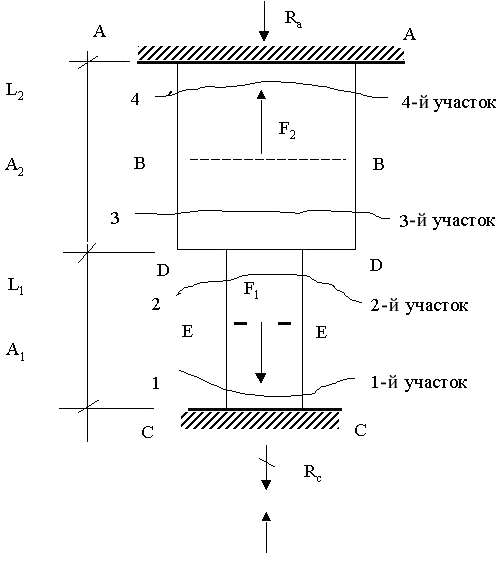
4. Разбиваем стержень на участки сечениями А-А, В-В. Д-Д, Е-Е и С-С (рис. 4). Имеем четыре участка.

5. Определяем продольные усилия на каждом участке стержня, используя метод сечений (рис. 6).

Участок I-I: F(у) = 0;

N₁ + R_с = 0;

N₁ = – R_с = – 45 кН.

Участок II-II: F(у) = 0;

N₂ + R_с – F₁ = 0;

N₂ = F₁ – R_с = 100 – 45 = 55 кН.

Участок III-III: F(у) = 0;

N₃ – F₁ + R_с = 0;

N₃ = F₁ – R_с = 100 – 45 = 55 кН.

Участок IV-IV: F(у) = 0;

–R_А – N₄ = 0;

N₄ = – R ₄= – 95 кН.

6. По найденным значениям продольных усилий строим эпюру силы N (рис.7,а).

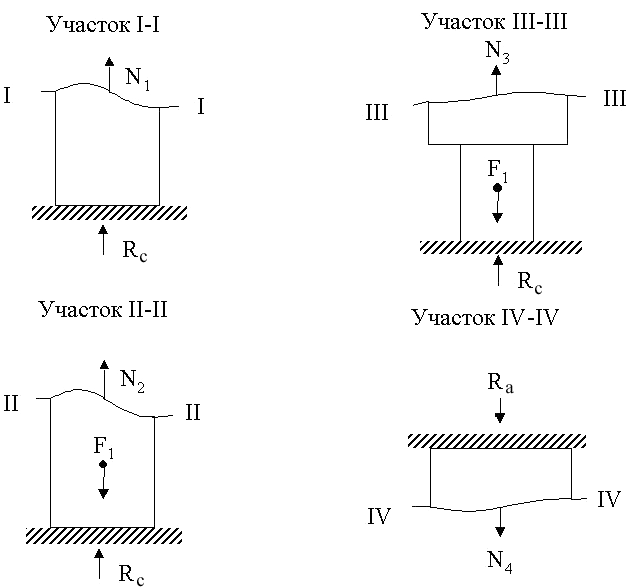
Рис. 6. Расчетные схемы к определению внутренних усилий по участкам стержня.

7. Определяем напряжения по участкам стержня:

₁ = N₁ / А₁= – 45 / 10 = – 4,5 кН/см²;

₂ = N₂ / А₁ = 55 / 10 = 5,5 кН/см²;

₃ = N₃ / А₂= 55 / 20 = 2,75 кН/см²;

₄ = N₄ / А₂= – 95 / 20 = – 4,75 кН/см².

8. По значениям напряжений на участках стержня строим эпюру напряжений  (рис. 7,б).

9. Определяем деформации отдельных участков стержня:

ℓ = Nℓ / EA = ℓ / E;

ℓ₁ = ₁ℓ₁ / 2E = – 4,5·100 / 2·10⁴ = – 0,0225 см;

ℓ₂ = ₂ℓ₁ / 2E = 5,5·100 / 2·10⁴ = 0,0275 см;

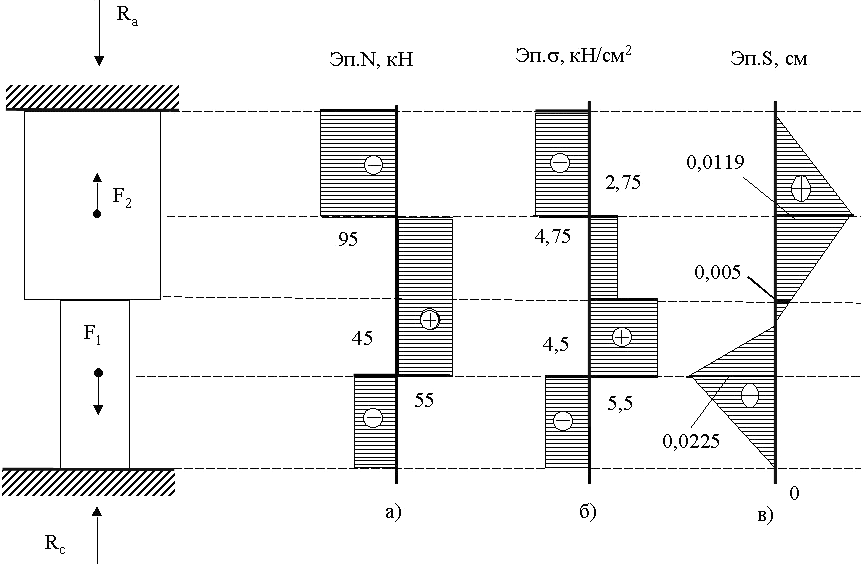
Рис. 7. Построение эпюр продольных сил N, напряжений  и перемещений S.

ℓ₃ = ₃ℓ₂ / 2E = 2,75·50 / 2·10⁴= 0,006875 см;

ℓ₄ = ₄ℓ₂ / 2E = – 4,75·50 / 2·10⁴= – 0,011875 см.

10. Вычисляем значения перемещений граничных сечений участков стержня, начиная расчет от нижней заделки:

S_ЕЕ = ℓ₁ = – 0,0225 см;

S_DD = S_ЕЕ + ℓ₂ = – 0,0225 + 0,0275 = 0,005 см;

S_BB = S_DD + ℓ₃ = 0,005 + 0,006875 = 0,011875 см;

S_AA = S_ВВ + ℓ₄ = 0,011875 – 0,011875 = 0.

11. По значениям перемещений граничных участков стержня строим эпюру перемещений (рис. 7,в).

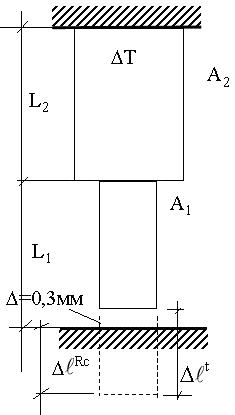
Задача 3. Исходные данные: двухступенчатый стержень с зазором (рис. 8) нагревается под действием температуры t = 60 ⁰С; материал – сталь 3;  = 0,3 мм; Е = 2·10⁴ кН/см²;  = 125·10^-7; А₁ = 10 см²; А₂ = = 20 см²; L₁ = 200 см; L₂ = 100 см.

Рис. 8. Расчетная схема стержня к задаче 3.

Решение. 1. Так как стержень с зазором, необходимо убедиться, что конструкция является статически неопределимой. Для этого мысленно отбрасываем нижнюю заделку и определяем общее удлинение стержня от действия температуры:

ℓ_t = ·t·(L₁ + L ₂) = 125·10^-7·60·

·(200 + 100) = 0,225 см.

Получили, что ℓ_t=2,25 мм  =0,3 мм.

Следовательно, при нагревании стержня зазор  = 0,3 мм будет перекрываться, и система является один раз статически неопределимой (рис.9).

2. Поскольку F(у) = 0; R_c – R_а = 0, то можем составить только одно уравнение статики с двумя неизвестными реакциями.

Определяем реакцию R_c (R_а = R_c), составляя дополнительное уравнение совместности деформаций:

ℓ^t + ℓ^Rc = .

Запишем составляющие этого уравнения:

ℓ^t = 0,225 см;

 = 0,03 см;

ℓ^Rc = – R_cL₁ / ЕА₁ – R_cL₂ / ЕА₂;

0,225 – R_cL₁ / ЕА₁ – R_cL₂ / ЕА₂ = 0,03;

0,225 – 0,03 = R_с(L₁ / EA₁ + L₂ / EA₂);

R_c = 0,195Е / (L₁ / A₁ + L₂ / A₂) = 156 кН.

R_а = R_c = 156 кН.

2. Используем метод сечений для определения продольных усилий по участкам стержня. Они постоянны на всех участках: N_i = R_c = – 156 кН (рис. 10,а).

Рис. 9. Схема к анализу деформации системы.

4. Вычисляем напряжения по участкам стержня и по найденным значениям _i строим эпюру напряжений  (рис. 10,б):

₁ = N / A₁ = – 156 / 10 = – 15,6 кН/см²;

₂ = N / A₂ = – 156 / 20 = – 7,8 кН/см².

5. Определяем деформации отдельных участков стержня:

ℓ₁ = ТL₁ – ₁L₁ / Е = 125·10^-7·60·200–– 15,6·200 / 2·10⁴ = – 0,006 см;

ℓ₂ = ТL₂ – ₂ L₂ / Е = 125·10^-7·60·

·100 – 7,8·100 / 2·10⁴ = 0,036 см.

6. По значениям деформаций вычисляем перемещения граничных сечений участков стержня, начиная расчет от заделки без зазора:

S_BB = ℓ₂ = 0,036 см;

S_СС = S_BB + ℓ₁ = 0,036 – 0,006 = 0,03 см.

6. По значениям перемещений граничных сечений участков стержня строим эпюру перемещений (рис. 10,в).

Задача 4. Исходные данные: двухступенчатый статически неопределимый стержень с зазором (рис. 11) находится под действием сосредоточенной и распределенной нагрузок; материал – сталь; зазор  = 0,1 мм; Е = 2·10⁴ кН/см²; А₁ = 10 см²; А₂ = 20 см²; L₁ = 200 см; L₂ = 100 см; F = 100 кН; q = 2 кН/см.

Решение. 1. Так как стержень с зазором, необходимо убедиться, что система является статически неопределимой. Для этого мысленно отбрасываем нижнюю заделку и определяем общее удлинение стержня от действия внешних сил F и q:

ℓ^F= (qL₁L₁ / 2) / EA₁ + qL₁L₂ / EA₂ – (FL₂/2) / EA₂ =

= (2200·200 / 2) / 210⁴10 +2200100 / 210⁴20 – 10050 / 210⁴20 =

= 0,2875 см.

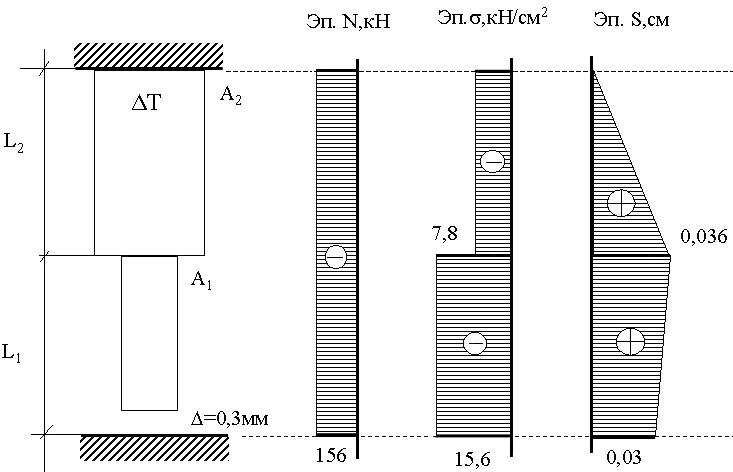
а) б) в)

Рис. 10. Построение эпюр продольных сил N, напряжений  и перемещений S.

Получили ℓ^F = 0,2875 см   = = 0,1 см. Следовательно, при нагружении стержня зазор  = 0,1 см будет перекрываться, и данная система будет статически неопределимой. Можем составить уравнение статики:

Рис. 11. Расчетная схема стержня к задаче 4.

F(у) = 0;

R_c+R_а + F – qL₁ = 0.

Это уравнение статики с двумя неизвестными реакциями. Следовательно, получили один раз статически неопределимую систему. Определяем реакцию R_c, мысленно отбросив для этого заделку СС, и составляем дополнительное уравнение совместности деформаций:

ℓ^F + ℓ^Rс =;

ℓ^F = 0,2875 см;  = 0,1 см;

ℓ^Rc = – R_cL₁ / EA₁ – R_cL₂ / EA₂;

0,2875 – 0,1 = R_c(L₁ / EA₁ + L₂ / EA₂);

R_c = 0,1875210⁴ / (200 / 10 +100 / 20) = 150 кН.

Аналогично определяем реакцию R_а

ℓ^F + ℓ^Rа=;

ℓ^F = (FL₂ / 2) / EA₂ + FL₁ / EA₁ – (qL₁L₁/2) / EA₁;

ℓ^Rа = R_аL₂ / EA₂ + R_аL₁ / EA₁;

FL₂ / 2EA₂ + FL₁ / EA₁ – qL₁² / 2EA₁ + R_а(L₂ / A₂ + L₁ / A₁) / Е = ;

R_а = E + qL₁² / 2A₁ – FL₂ / 2A₂ – FL₁ / A₁ / (L₁ / A₁ + L₂ / A₂)=0,1210⁴ +

+ 2200² / 210 – 100(100 / 220 + 200 / 10) / (200 / 10 + 100 / 20) =150 кН.

Проводим проверку правильности определения реакций:

F(у) = 0;

R_с + R_а + F – qL₁ = 0;

150 + 150 + 100 – 2·200 = 0;

400 – 400 = 0.

Следовательно, реакции определены правильно.

2. Разбиваем стержень на участки с границами АА; ВВ; СС и ДД.

3. Используя метод сечений, определяем продольные усилия на каждом участке стержня (рис. 12).

Участок АД (0  Z₁  50 cм):

F(у) = 0;

N₁ = R_а = 150 кН.

Участок ДВ (0  Z₂  50 cм):

F(у) = 0;

R_а + F – N₂ = 0;

N₂ = R_а + F = 150 + 100 = 250 кН.