Сложение в дополнительном коде

6 + (-4) = 2 при сложении перенос из знакового разряда не учитывается.

Если в знаковом разряде «0» – то число положительное в прямом коде, если же в знаковом разряде «1» – то результат представлен в дополнительном коде.

• Представить в дополнительном коде десятичные числа:

Число	Ответ
-37	1111111111011011
-86	1111111110101010
-165	1111111101011011
-516	1111110111111100
-2433	1111011001111111

Для перехода из дополнительного кода в прямой, разряды так же инвентируются и добавляется «1» в младший разряд.

При сложении можно использовать и обратный код, а дополнительную «1» учитывать добавлением в результат.

Сложение двоично-кодированных десятичных чисел

Для представления всех цифр от 0 до 9 нужно 4 разряда.

При кодировании десятичных цифр используется 10 кодовых операций, остальные 6 операций – либо для обозначения знака (например, 1111), либо для других целей.

8 4 2 1 (2³ 2² 2¹ 2⁰) – весовой код

2 4 2 1 – код с избытком 3.

Правило:

• если 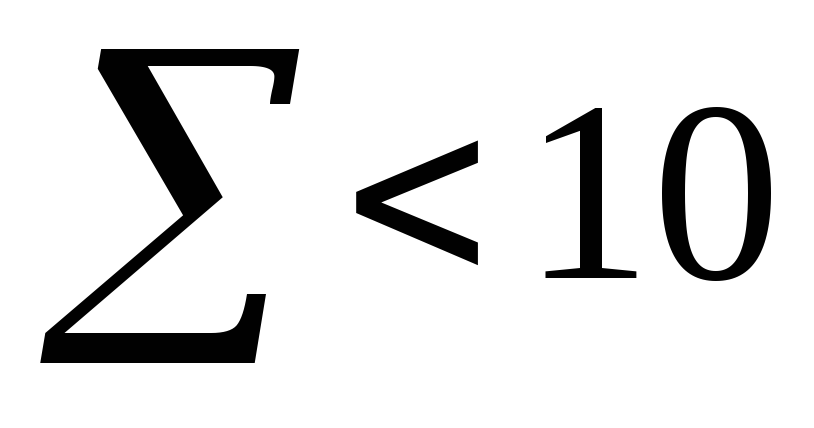, то суммирование десятичных цифр идёт по обычным правилам;

• если 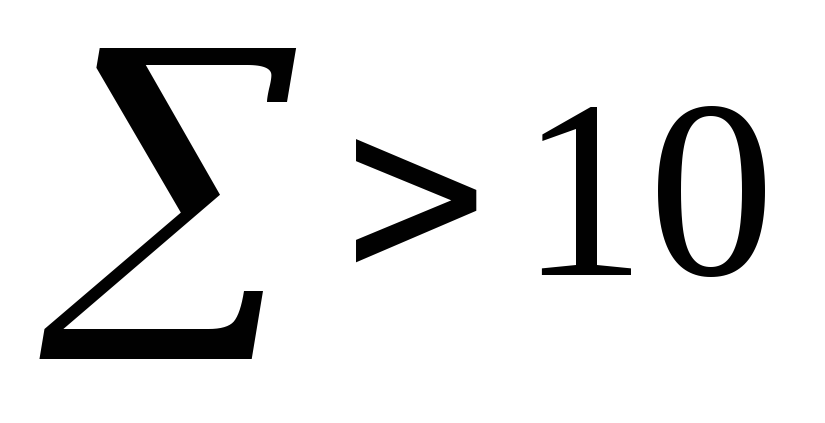, то нужна коррекция полученного результата. Коррекция осуществляется прибавлением шести единиц к полученному результату (код 0110).

Признаком того, что , является:

1. перенос из весового разряда 8 (из 4-го);

2. наличие двух «1» в весовых разрядах одновременно: 8 и 4 или 8 и 2.

Формы представления чисел в эвм

1. Целые числа

х

В разрядной сетке ЭВМ записываются целые числа во всех разрядах, кроме старшего, старший разряд – это знаковый.

- диапазон целых чисел;

где: n – число разрядов.

Ошибка (шаг кванта числа) обратно пропорциональна самому старшему числу:

В зависимости от числа используемых разрядов диапазон чисел и ошибка связаны соотношением:

Длина слова	4 бит	8	12	16
Диапазон	15	255	4095	65535
Квант ошибки	0,0666	0,00392	0,000298	0,00002
Ошибка квантования, %	3,33	0,196	0,012	0,001

2. Действительные числа

а) числа с фиксированной точкой:

Один разряд – знаковый (как правило, старший), остальные кодируют число.

Десятичная точка отделяет целую часть числа.

Точка может стоять:

• перед старшим разрядом;

• после младшего разряда.

Пример: число –0,101101₂

1	1011010 00000000

старший 1 байт 2 байт

разряд (знак) старшие младшие

разряды разряды

При занесении числа в память (допустим) младшие разряды (свободные) заполняются нулями. В таком виде хранится только дробная часть числа, поэтому необходимо масштабирование при работе с числами больше «1».

Недостатки: масштабирование

Достоинства: более высокая точность при малых значениях числа.

Нули в старших разрядах приводят к уменьшению числа значимых разрядов (т.е. необходима нормализация, масштабирование, чтобы в старшем разряде была «1»).

• точка в младшем разряде:

1101,0

0	0000000 00110011

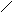
Знак 1 байт 2 байт

Не используемые разряды (старшие) заполняются нулями.

Это форма целых чисел

б) числа с плавающей точкой.

Число, как десятичное, так и двоичное, представляется в показательной форме.

• 685,73 = 0,68573  10³, где 3 – порядок степени

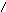
мантисса основание

• 0,000101101₂ = 0,101101  10^-11

Запись числа в машинном разряде:

0

1011010

1

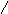
11

Знак мантисса знак порядок

числа порядка

При хранении (записи) чисел с плавающей точкой их всегда нормализуют так, чтобы старший разряд мантиссы был (это делается путём изменения порядка, т.е. степени).

При выполнении операций над числами с плавающей точкой операции выполняются в нормализованной форме (особенно умножение и деление), или эти числа переводятся в обычный двоичный формат.