Преобразование чисел из одной системы счисления в другую.

1. перевод чисел в десятичную систему.

Х₂ Х₁₀

Для перевода из других систем счисления в десятичную, вычисляем полином (2)

Примеры:

1110,01₂;

1101101₂ =>1·2⁶ + 1·2⁵ + 0·2⁴ + 1·2³ + 1·2² + 0·2¹ + 1·2⁰ = 1·64 + 1·32 + 0·16 + 1·8 + 1·4 + 0·2 + 1·1 = 109₁₀;

27,5₈;

А3,В₁₆.

2. перевод чисел из десятичной в другие системы счисления.

а) перевод целой части:

Выделим целую часть:

Далее разделим целую часть числа на основание, получим:

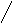
значение числа в младшем разряде

остаток

Остаток делим на основание, получаем значение числа d₁ и остаток, и так далее, пока не получим последнюю цифру d_n-1 (d_i<b).

б) преобразование дробной части:

Выделяем отдельно дробную часть числа:

Далее умножаем дробную часть на основание:

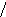
значение числа остаток

в 1-ом разряде

Остаток умножаем на основание b, получаем b_-2 и остаток, и так далее, пока остаток не станет нулевым, или пока не будет достигнута требуемая точность представления числа.

Пример 1:

52,75₁₀ в двоичную систему счисления;

а) 52 : 2 = 26 – остаток 0 (младшая цифра)

26 : 2 = 13 – остаток 0

13 : 2 = 6 – остаток 1

6 : 2 = 3 – остаток 0

3 : 2 = 1 – остаток 1

1 : 2 = 0 – остаток 1 (старшая цифра)

б) 0,75 х2 = 1,5 – остаток 1

0,5 х 2 = 1 – остаток 1 (младшая цифра);

Пример 2:

123,12₁₀в восьмеричную систему счисления.

а) 123 : 8 = 15 – остаток 3

15 : 8 = 1 – остаток 7

1 : 8 = 0 – остаток 1

б) 0,12 х 8 = 0,96 – остаток 0

0,96 х 8 = 7,68 – остаток 7

0,68 х 8 = 5,44 – остаток 5

0,44 х 8 = 3,52 – остаток 3, и т.д.

Тогда, 123,12₁₀ 173,0753₈

Прямое и обратное двоично-восьмеричное преобразование

Правило: для перевода Х₂Х₈ достаточно исходное двоичное число разбить на тройки двоичных чисел и каждой тройке поставить в соответствие восьмеричный эквивалент.

001010011,011010 приписываем недостающие нули

В старшем разряде недостающие цифры дополняются нулями, в дробной части недостающие цифры также дополняются нулями.

Следовательно, 123,32₈.

Для перевода Х₈Х₂ к каждой восьмой цифре ставится двоичный эквивалент:

373,5₈ 011 111 011, 101

Преобразование Х₂ Х₁₆, Х₁₆ Х₂.

Двоичное число разбивается на тетрады (четвёрки) и каждой тетраде в соответствие ставится шестнадцатеричный эквивалент; а при преобразовании Х₁₆ Х₂ каждому шестнадцатеричному числу ставится в соответствие двоичная тетрада.

Пример:

1. Х₂ Х₁₆:

0001 1111 0010,1010 1000 1F2,A8₁₆;

2. Х₁₆ Х₂:

ABC,DE₁₆ 1010 1011 1100, 1101 1110.

3. Представить двоичное число 1010110101111 в восьмеричной системе счисления.                                                            1   010   110   101   111                                                            1     2       6       5       7 4. Представить двоичное число 1010110101111 в шестнадцатеричной системе счисления.                                                            1   0101   1010   1111                                                            1      5         A         F

    Решение примеров.     1) Перевести числа из двоичной системы счисления в восьмеричную и шестнадцатеричную: 11100011; 101110,1; 111111,01001.     2) Перевести числа из восьмеричной системы счисления в двоичную: 567; 204,72.     3) Перевести числа из шестнадцатеричной системы счисления в двоичную: 4D2A; 31,05; 40A,7.

    Задача 1. Перевести число 76,5 из восьмеричной системы счисления в шестнадцатеричную.     Задача 2. Перевести число 7142 из десятичной системы счисления в шестнадцатеричную.     Задача 3. Перевести число 0,225 из десятичной системы счисления в шестнадцатеричную.     Задача 4. Перевести число 440 из десятичной системы счисления в двоичную.     Задача 5. Перевести число 110,175 из десятичной системы счисления в восьмеричную.     Задача 6. Перевести число 9F3A из шестнадцатеричной системы счисления в десятичную.