Основы двоичной арифметики

1. Сложение: 0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 1 (перенос в старший разряд)

• Пример сложения многоразрядных чисел. Сложение чисел в двоичной системе счисления.     Запись:         2            10            0000000000000010       +3     +11     + 0000000000000011     5            101          0000000000000101

• Требуется сложить два числа 18₁₀ и 23₁₀

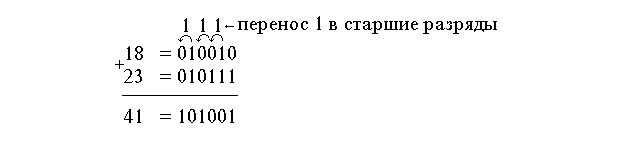
    При сложении чисел надо обязательно проговаривать алгоритм сложения. Следует учитывать, что сложение, как обычно, нужно начинать с младшего разряда. Если сумма единиц разряда окажется равной или большей основания системы счисления, то возникает перенос единицы в старший разряд. После сложения cледует обязательно сделать обратный перевод и убедиться, что число 101 — действительно число 5 в десятичной системе счисления.

2. Вычитание: 0 – 0 = 0

1 – 1 = 0

1 – 0 = 1

0 – 1 = 1 заём из старшего разряда

Вычитание двоичных чисел. В компьютере вычитание заменяется сложением с отрицательным числом, представленным в дополнительном коде.     Запись:       14            1110          0000000000001110        -9    +1001   +1111111111110111   5            101           10000000000000101

    Так как под целое число отводится 16 разрядов, то старшая единица теряется. Ответ получается 101.

3. Умножение: 0 х 0 = 0

1 х 0 = 0

0 х 1 = 0

1 х 1 = 1

Умножение чисел в двоичной системе счисления.                                         110                                       *101                                           110                                    + 000                                      110                                          11110

Подчеркиваем, что при умножении 1•1 = 1 и 1•0 = 0. Анализируя примеры умножения в двоичной системе счисления, необходимо обратить внимание учащихся на важную особенность выполнения этой операции в данной системе счисления. Так как очередная цифра множителя может быть только 1 или 0, то промежуточное произведение равно либо множимому, либо 0. Таким образом, операция умножения в двоичной системе фактически не производится: в качестве промежуточного произведения записывается либо множимое, либо 0, а затем промежуточные произведения суммируются. Иначе говоря, операция умножения заменяется последовательным сложением.

Двоичные числа со знаком

При выполнении различных операций в современных цифровых устройствах и системах числа обычно представляются в двоичной системе счисления. Это связано с тем, что для представления смысла символов цифр двоичной системы счисления можно использовать простые электронные схемы с двумя электрическими состояниями. Принято, что символ “1” представляется некоторым стандартным уровнем напряжения или тока, а “0” - нулевым или близким к нулю уровнем напряжения или тока.

Арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными, однако, с целью упрощения цифровых систем для выполнения арифметических операций применяют алгоритмы, отличные от алгоритмов действий десятичной арифметики.

В двоичной системе счисления для представления знака числа используется дополнительный знаковый разряд (один или несколько разрядов), который располагается перед старшим числовым разрядом. Для положительных чисел значение знакового разряда Зн.р.=0, для отрицательного числа Зн.р.=1.

Операция вычитания в цифровых системах реализуется с помощью операции сложения. Вычитаемое при этом представляется в дополнительном коде (если расчет не требует высокой точности - в обратном коде).

Двоичный код со знаком называют также прямым кодом. В качестве примера рассмотрим положительное и отрицательное числа, десятичный эквивалент которых равен 46₁₀.

Обратный код получается путем замены всех “0” на “1” и всех “1” на “0” прямого кода (двоичного числа со знаком). Причем, знаковый разряд при этом остается неизменным.

Замена “0” на единицу (“1”) называется инвертированием (также и замена “1” на “0”).

Обратный код, дополненный единицей в младшем разряде, называется дополнительным кодом. Последовательность действий при получении дополнительного кода:

Обратный и дополнительный коды позволяют использовать вместо вычитания операцию сложения, при этом результат автоматически получается нужный.

Десятичное число	Прямой код	Обратный код	Дополнит. код
+7	0111	0111	0111
+6	0110	0110	0110
+5	0101	0101	0101
+4	0100	0100	0100
+3	0011	0011	0011
+2	0010	0010	0010
+1	0001	0001	0001
0	0000	0000	0000
	1000	1111	1111
-1	1001	1110	1111
-2	1010	1101	1110
-3	1011	1100	1101
-4	1100	1011	1100
-5	1101	1010	1011
-6	1110	1001	1010
-7	1111	1000	1001
-8	11000	10111	1000