
- •Методические указания
- •Вероятностные модели в задачах теории информации
- •1.1. Случайные события. Вероятность
- •1.2. Дискретная и непрерывная случайные величины
- •1.3. Задачи
- •1.4. Контрольные вопросы
- •2. Информационная мера шеннона.
- •2.1. Количество информации и избыточность.
- •2.2. Энтропия непрерывных сообщений
- •2.3. Задачи
- •2.4. Контрольные вопросы
- •3. Условная энтропия и взаимная информация
- •3.1. Дисктретные системы передачи информации.
- •3.2. Непрерывные системы передачи информации.
- •3.3. Задачи
- •3.4. Контрольные вопросы
- •Список использованных источников
- •Значение функции
- •654600 «Информатика и вычислительная техника» и направления подготовки бакалавров 552800 «Информатика и вычислительная техника».
- •450000, Уфа-центр, к. Маркса, 12
2.2. Энтропия непрерывных сообщений
Непрерывные
системы
передачи информации - системы, в которых
как реализации сообщения, так и реализации
сигнала на конечном временном интервале
![]() представляют собой некоторые непрерывные
функции времени.
представляют собой некоторые непрерывные
функции времени.
Пусть
![]() - реализации непрерывного сообщения на
входе какого-либо блока схемы связи,
- реализации непрерывного сообщения на
входе какого-либо блока схемы связи,![]() - реализация выходного сообщения
(сигнала),
- реализация выходного сообщения
(сигнала),![]() - плотность вероятности ансамбля входных
сообщений,
- плотность вероятности ансамбля входных
сообщений,![]() - плотность вероятности ансамбля выходных
сообщений
- плотность вероятности ансамбля выходных
сообщений
Формулы
для энтропии
![]() непрерывных сообщений получаются путем
обобщения формул для энтропии дискретных
сообщений. Если
непрерывных сообщений получаются путем
обобщения формул для энтропии дискретных
сообщений. Если![]() - интервал квантования (точность
измерения), то при достаточно малом
- интервал квантования (точность
измерения), то при достаточно малом![]() энтропия непрерывных сообщений
энтропия непрерывных сообщений
![]()
где
![]() По аналогии
По аналогии![]()
Пример
1. По линии
связи передаются непрерывные
амплитудно-модулированные сигналы
![]() распределенные по нормальному закону
с математическим ожиданием
распределенные по нормальному закону
с математическим ожиданием![]() и дисперсией
и дисперсией![]()
Определить
энтропию
![]() сигнала при точности его измерения
сигнала при точности его измерения![]()
Решение.
По условию плотность вероятности сигнала
![]()
![]()
![]()
![]()
![]()
Подставляя числовые значения, получаем
![]() дв.
ед.
дв.
ед.
2.3. Задачи
2.3.1.
Определить энтропию источника информации
![]() ,
передающего сообщения
,
передающего сообщения![]() ,
,![]() Вероятность сообщений определяются по
формулам:
Вероятность сообщений определяются по
формулам:
![]()
![]()
![]()
![]()
Известно, что в сообщении источника 100 символов. Определить, сколько символов потребуется для передачи этой информации при использовании безызбыточного алфавита той же размерности;
2.3.2. На выходе источника сообщений может появляться нуль и единица. Вероятность появления каждого сообщения изменяется со временем и в каждый момент времени может быть определена по формулам:
![]()
Необходимо исследовать изменение энтропии источника информации во времени и определить момент времени, когда математическая модель опыта теряет смысл. Энтропия источника сообщений вычисляется в соответствии с формулой Шеннона. Все вычисления сводятся в таблицу:
|
|
Таблица 2 | |||||
|
t |
P(0) |
P(1) |
H(0) |
H(1) |
H | |
|
|
|
|
|
|
| |
Значения
![]() задаются целыми числами через равные
промежутки времени
задаются целыми числами через равные
промежутки времени![]()
Математическая
модель опыта имеет смысл, когда выполняются
соотношения для вероятностей
![]()
![]()
![]()
Значения
![]() ,
при котором эти соотношения перестают
выполняться, и есть момент времени,
когда модель опыта теряет смысл.
,
при котором эти соотношения перестают
выполняться, и есть момент времени,
когда модель опыта теряет смысл.
После
заполнения таблицы результатами
вычислений следует построить графики
изменения
![]()
![]()
![]()
При анализе графиков обратить внимание на точку, где энтропия принимает наибольшее значение и наименьшее значение. Указать значения вероятностей появления символов в этих точках и моменты времени.
2.3.3.
Определить значение энтропии
![]() по заданным аналитическим выражениям
плотности вероятности
по заданным аналитическим выражениям
плотности вероятности![]() :
:
1) для равномерного (прямоугольного) закона распределения:
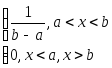 ,
,
2) для Гауссовского (нормального) закона распределения:
![]() ,
,
3) для Симпсоновского (треугольного) закона распределения:
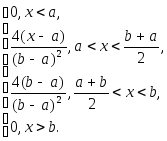
2.4. Контрольные вопросы
2.4.1. Дать определение энтропии.
2.4.2. Как связаны между собой формулы Хартли и Шеннона?
2.4.3. Может ли энтропия быть отрицательной?
2.4.4. В каких случаях энтропия равна нулю?
2.4.5. При каких условиях энтропия принимает максимальное значение?
2.4.6. В чем состоит правило сложения энтропий для независимых источников?
2.4.7. Что понимают под непрерывными системами передачи?
2.4.8. Как определить количество информации непрерывных сообщений?
