1. Информационная мера шеннона.

   1. Количество информации и избыточность.

Дискретные системы связи - системы, в которых как реализации сообщения, так и реализации сигнала представляют собой последовательности символов алфавита, содержащего конечное число элементарных символов.

Пусть  и  - случайные величины с множествами возможных значений Х={х₁,х₂,...,х_N}, Y={y₁,y₂,...,y_M}

Количество информации H() при наблюдении случайной величины   X = {x₁,x₂,…,x_N} с распределением вероятностей P={p₁,p₂,…р_N}задается формулой Шеннона:

.

Единицей измерения количества информации является бит, который представляет собой количество информации, получаемое при наблюдении случайной величины, имеющей два равновероятных значения. При равномерном распределении р₁=р₂=…=p_N количество информации задается формулой Хартли:

Справедливы следующие соотношения:

• 0 H()log₂N;

• N=2, p1=p2=0.5, H()=1;

• H(,)=H()+H(), если  и  -независимы. Избыточностью называется р = 1‑H(,)/max{ H() } = 1 ‑ H()/log₂N.

2. Пример.

Источник сообщений выдает символы из алфавита А = {а_i}, i = 1..4 с вероятностями р₁ = 0.2, р₂  = 0.3; р₃  = 0.4; р₄ = 0.1. Найти количество информации и избыточность.

Решение. По формуле Шеннона

Н(А) = -0.2 log₂ 0.2 – 0.3 log₂ 0.3 – 0.4 Iog₂ 0.4 – 0.1 log₂ 0.1 = 1.86 (бит).

По определению избыточности р = 1 – H(A)! log₂ 4 = 0,07.

3. Задачи

Задача 1. Определить энтропию и избыточность источника информации А, передающего сообщения А_i, i = 1..4. Вероятность сообщений определяются по формулам: р₁ = 0.2 + 0.005^.V; р₂ = 0.3 ‑ 0.005^.V; р₃ = 0.1 + 0.01^.V; р₄ = 0.4 ‑ 0.01^.V, где V – номер варианта.

Задача 2. На выходе источника сообщений может появляться нуль и единица. Вероятность появления каждого сообщения изменяется со временем и в каждый момент времени может быть определена по формулам:

p(1) = 0.9 – 0.02^.(V - 1) – 0.1^.t, p(0) = 0.1 + 0.02^.(V - 1) + 0.1^.t,

Необходимо исследовать изменение энтропии источника информации во времени и определить момент времени, когда математическая модель опыта теряет смысл. Энтропия источника сообщений вычисляется в соответствии с формулой Шеннона. Все вычисления сводятся в табл.2:

Таблица 2

t	Р(0)	Р(1)	H(0)	Н(1)	H

Значения t задаются целыми числами через равные промежутки времени t = 0,1,2,...

Математическая модель опыта имеет смысл, когда выполняются соотношения для вероятностей р(1) + р(0) = 1; 0 р(0)  1; 0  р(1)  1. Значенияt, при котором эти соотношения перестают выполняться, и есть момент времени, когда модель опыта теряет смысл. После заполнения таблицы результатами вычислений следует построить графики измененияH(0),H(1),H. При анализе графиков обратить внимание на точку, где энтропия принимает наибольшее значение и наименьшее значение. Указать значения вероятностей появления символов в этих точках и моменты времени.

Задача 1

Сигнал подается на вход канала (величина ) с вероятностью(логическая единица) и отсутствует (логический ноль) с вероятностью (1 –р). Вероятность того, что поступившая единица правильно воспроизведена на выходе –p^.0.8, а вероятность правильного воспроизведения нуля –p^.0.95(величина). Найти энтропию выхода, энтропию входа, взаимную информацию входа и выходаI(S,S');

Задача 2

Распределение вероятностей входных и выходных сигналов системы заданы следующей матрицей:

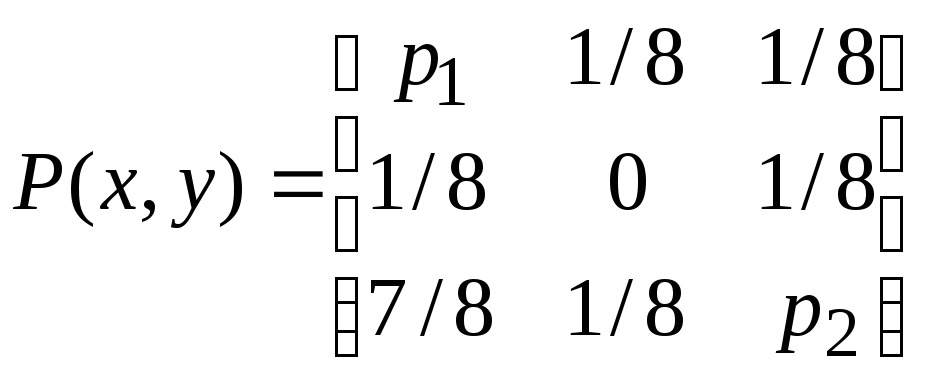, где

Определить энтропию входа H(Y ), условную энтропию H(Y/X ) и Н(Х/Y ), взаимную информацию I (X,Y ).