11. Вычислим внутренние усилия. Вычисления сведем в таблицу.

Поперечная сила .

Изгибающий момент

Крутящий момент при свободном кручении

Бимомент

Крутящий момент при стесненном кручении

В случае действия на стержень сосредоточенной силы, во всех сечениях должно выполняться условие:

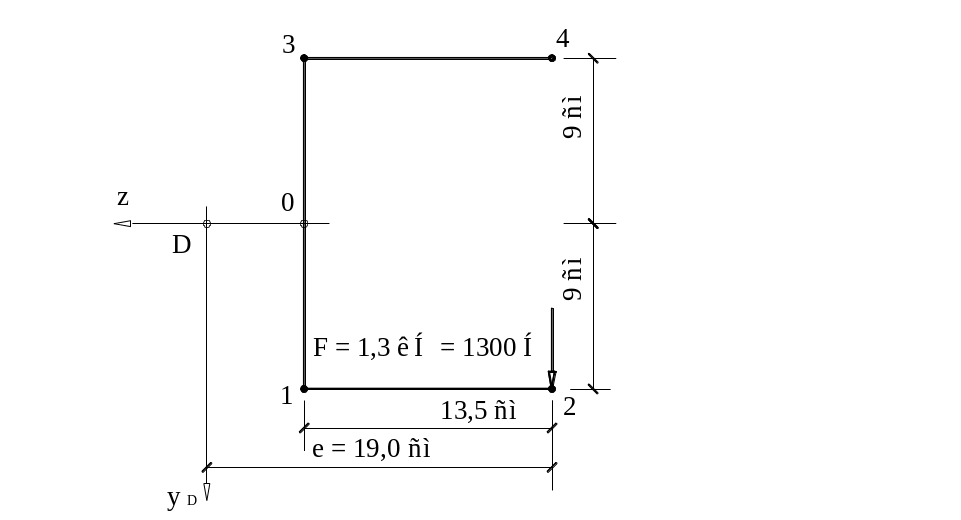
_{Рис. 15}

	0
	0	0,5	1	1,5	2
	-1300	-1300	-1300	-1300	-1300
	0	-650	-1300	-1950	-2600
	0	27,28	63,37	119,94	215,24
	195,18	186,81	159,01	102,79	0
	51,8	60,17	87,97	144,19	246,98

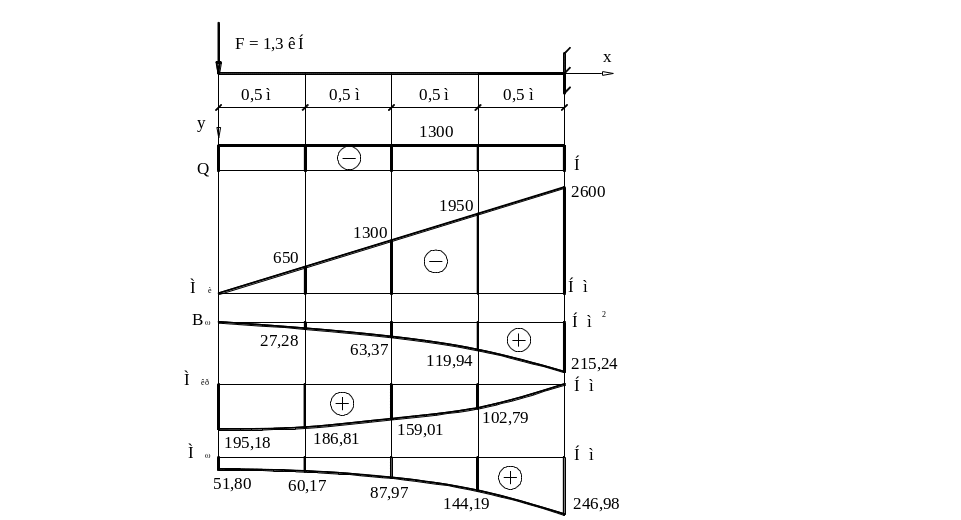_{Рис. 16}

12. Вычислим нормальные напряжения в опасном сечении ( ):

Для этого умножим эпюру на эпюру на и сложим их алгебраически.

Вычислим константы:

_{Строим эпюры нормальных напряжений}

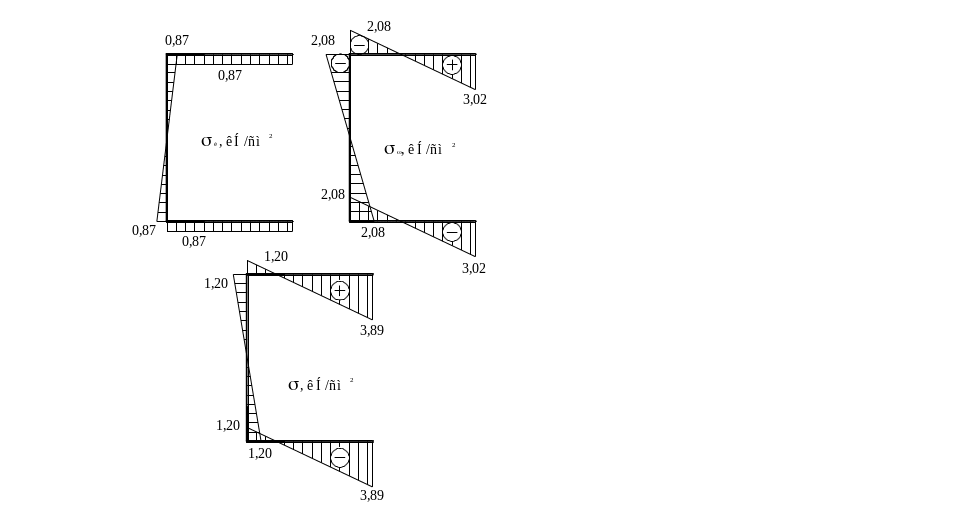
_{Рис. 17}

ПРИМЕР № 2

Расчет тонкостенного стержня открытого профиля.

Характеристики материала:

Схема сечения №4; точка приложения силы 3;

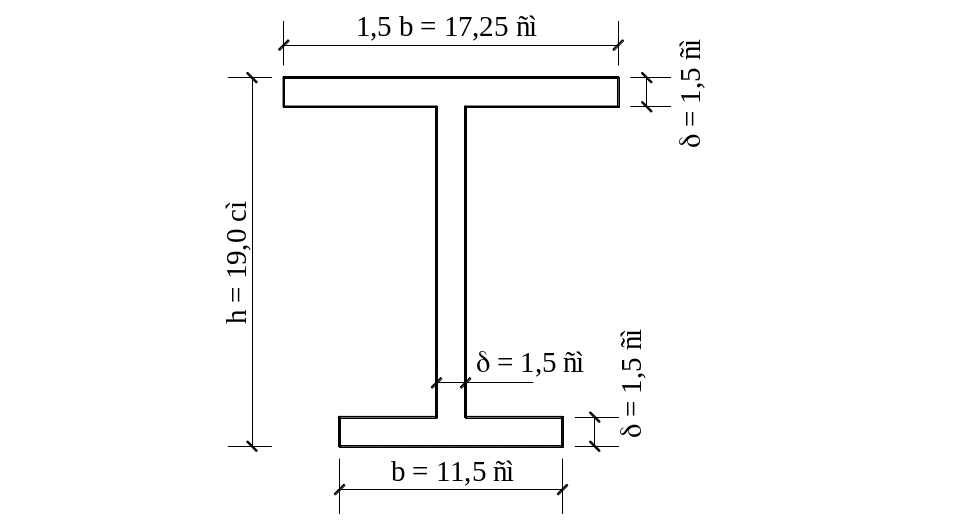
Рис. 18

Решение

1. Разбиваем фигуру на простейшие, определяем площади прямоугольников.

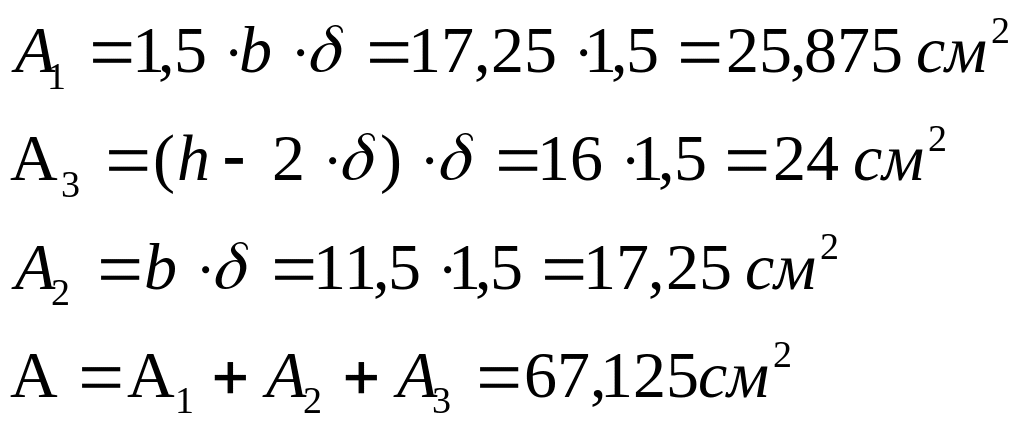
2. Определяем положение центра тяжести сечения относительно осей

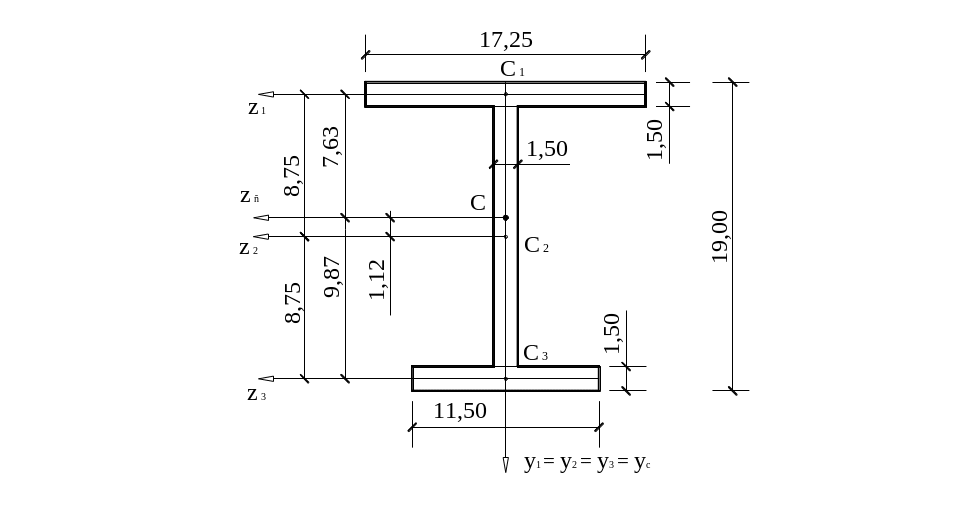
Рис. 19

, т.к. - ось симметрии

3. Вычисляем главные центральные моменты инерции

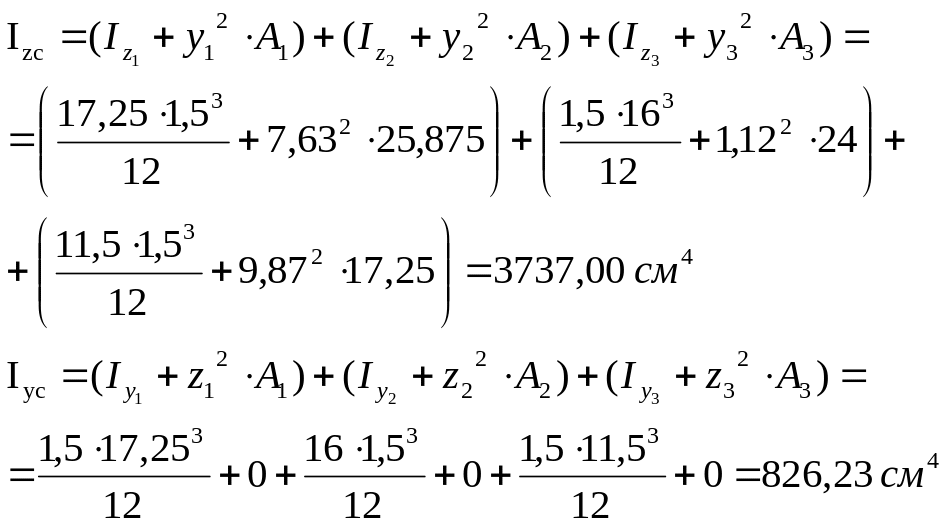
4. Вычисляем секториальную площадь.

Заменяем двутавр расчётной схемой, совпадающей с осевыми линиями сечения. Строим эпюры координат z и y.

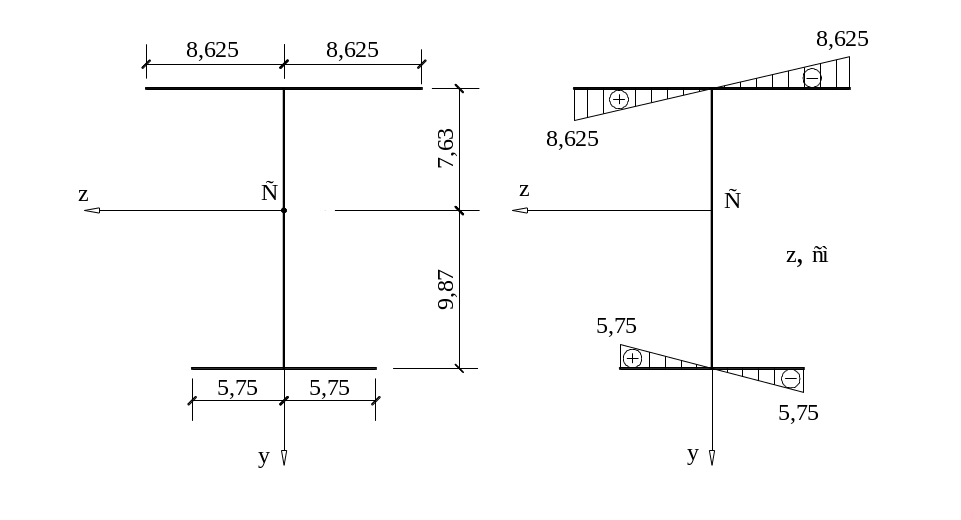Рис. 20 Рис. 21

Рис. 22

Строим эпюру секториальной площади (полюс выбираем в центре тяжести сечения P = C). 0 – начало отсчета секториальной площади (совпадает с центром тяжести).

,

z y

Координаты 1 ( 5,75 ; 9,87)

точек 2 ( -5,75; 9,87)

относительно 3 ( 8,625;-7,63)

центра 4 (-8,625;-7,63)

тяжести 5 ( 0 ; 9,87)

6 ( 0; -7,63)

0 ( 0; 0 )

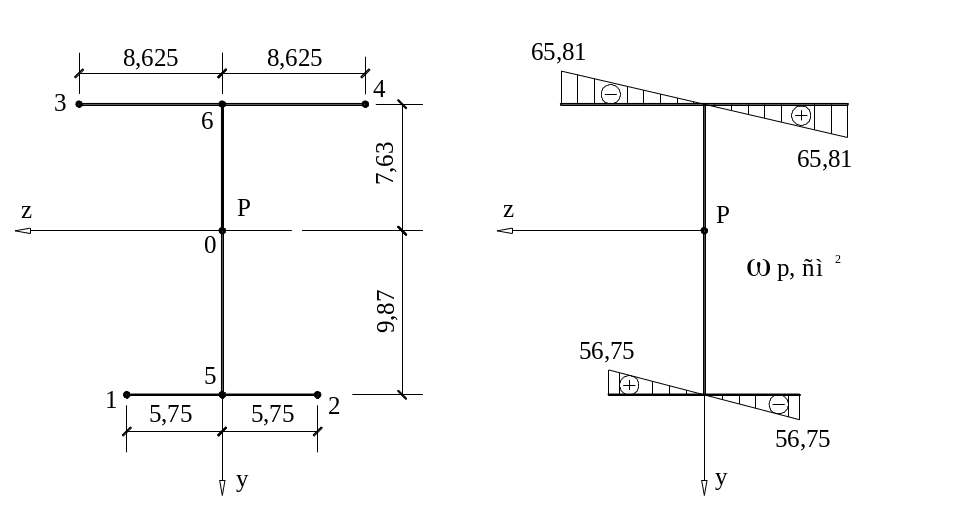Рис. 23 Рис. 24

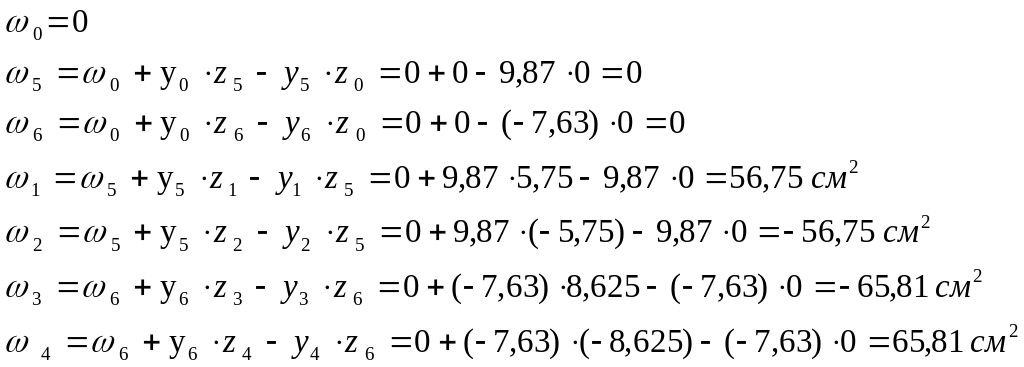
5. Определяем положения центра изгиба.

Сначала вычисляем секториально-линейные статические моменты, для этого умножаем эпюру на соответствующие эпюры координат (по способу Верещагина).

(при умножении симметричной эпюры на кососимметричную результат равен 0).

Определяем положения центра изгиба.

6. Строим эпюру главной секториальной площади (полюс помещаем в центр изгиба P = D). 0 – начало отсчета секториальной площади (совпадает с центром изгиба).

z y

Координаты 1 ( 5,75 ; 12,31)

точек 2 ( -5,75; 12,31)

относительно 3 ( 8,625;-5,19)

центра 4 (-8,625;-5,19)

изгиба 5 ( 0 ; 12,31)

6 ( 0; -5,19)

0 ( 0; 0 )

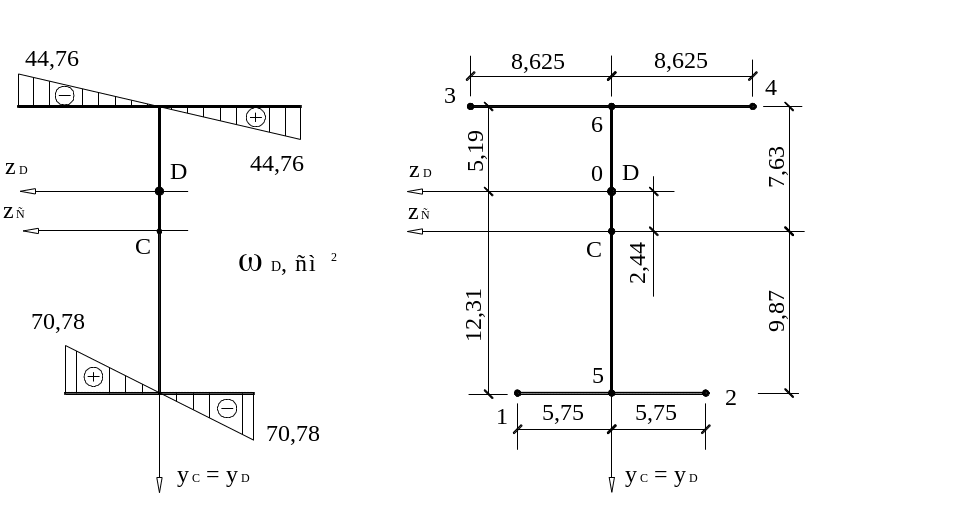Рис. 25 Рис. 26

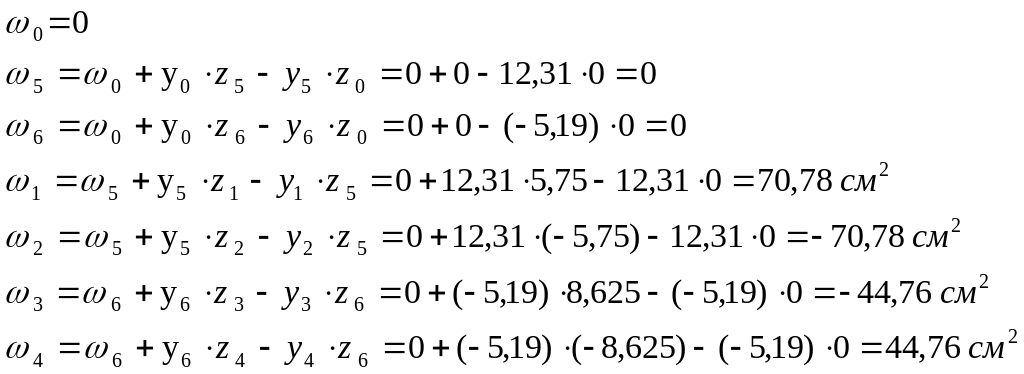
7. Вычисляем секториальный момент инерции .

Для этого перемножаем эпюру на эпюру . (по способу Вере-

щагина и формуле Симпсона).

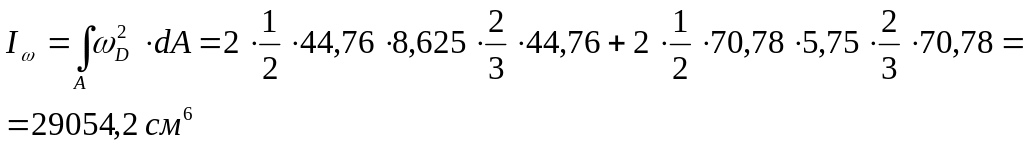
8. Вычислим момент инерции при чистом кручении

, где

– меньший размер,

– размер по осям,

- для двутавра.

9. Вычислим изгибно-крутильную характеристику

Предварительно вычислим модуль сдвига:

Изгибно-крутильная характеристика:

10. Дифференциальное уравнение углов закручивания

, или

, где

– угол закручивания,

– интенсивность внешней распределённой крутящей нагрузки с учётом знака (знак «плюс» когда нагрузка стремится вращать против часовой стрелки при взгляде с положительного направления оси х )

Решение уравнения:

Произвольные постоянные зависят от граничных условий

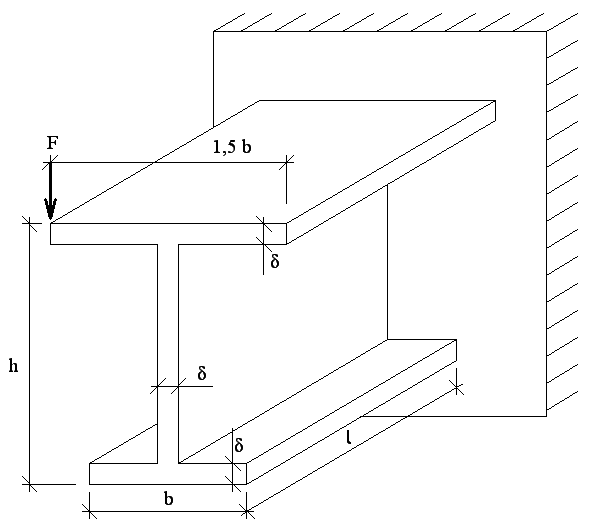
_{Рис. 27}

Запишем граничные условия

Для свободного торца ( )

или

Для защемленного торца ( )