МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЕЖИ И СПОРТА УКРАИНЫ

Одесская государственная академия строительства и архитектуры

Кафедра сопротивления материалов

Неутов С.Ф., Карпюк Ф.Р., Крантовская Е.Н.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

РАСЧЕТ КОРОТКИХ ВНЕЦЕНТРЕННО СЖАТЫХ СТЕРЖНЕЙ

к расчетно-графической работе

по курсу “Сопротивление материалов”

для студентов направления 6.060101 «Строительство»

Одесса – 2011 год

УДК 539(07)

«УТВЕРЖДЕНО»

Ученым советом

Инженерно-строительного

института ОГАСА

(протокол №3 от 24.11. 2010 р.)

Методические указания рассмотрены и рекомендованы в печать на заседании научно-методической комиссии специальности ПГС ОГАСА (протокол №3 от 22. 11. 2010 г.).

Методические указания рассмотрены и рекомендованы в печать на заседании кафедры сопротивления материалов ОГАСА (протокол №3 от 10.11.2010 г.).

Приводятся краткие теоретические сведения по данному разделу курса, приведены примеры решения задач и исходные данные для выполнения расчетно-графических работ.

Составители: к.т.н., доц. Неутов С.Ф.,

к.т.н., доц. Карпюк Ф.Р.,

к.т.н., доц. Крантовская Е.Н.

Рецензенты: заведующий кафедрой теоретической и прикладной механики Одесского национального морского университета, д.т.н., проф. Гришин В.А.;

профессор кафедры динамики, прочности машин и сопротивления материалов Одесского национального политехнического университета, д.т.н., проф. Оробей В.Ф.

Ответственный за выпуск:

заведующий кафедрой сопротивления материалов ОГАСА,

д.т.н., профессор Гришин А.В.

Внецентренное сжатие является одной из наиболее характерных деформаций для многих элементов строительных конструкций.

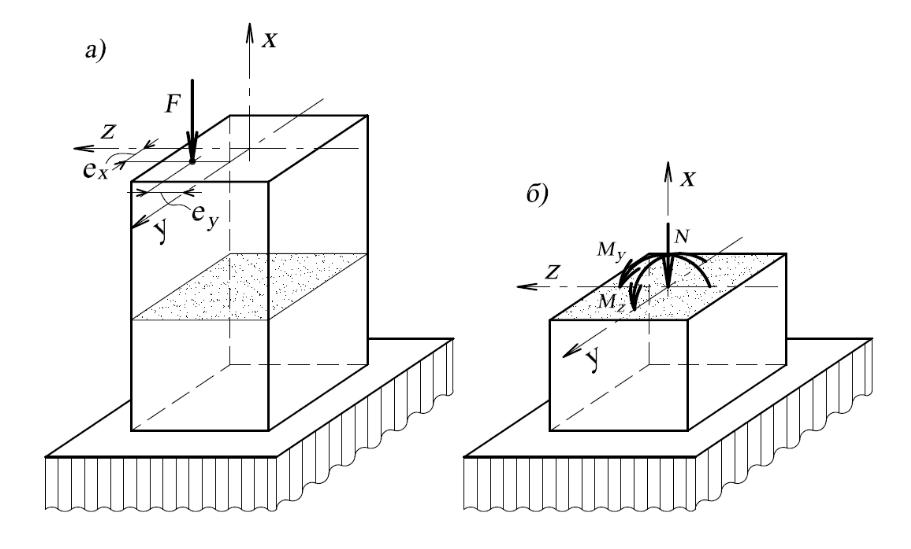
Рис.1.

В любом поперечном сечении стержня при внецентренном сжатии возникают три силовых фактора (рис 1б)

(1)

где: - координаты точки (полюса) приложения внешней силы F, или эксцентриситеты внешней силы относительно главных центральных осей поперечного сечения.

Таким образом, общий случай внецентренного сжатия сводится к центральному (осевому) сжатию силой в сочетании с чистым косым изгибом. Последний, как известно, можно представить в виде двух чистых прямых изгибов во взаимно перпендикулярных плоскостях .

Нормальные напряжения, возникающие в поперечном сечении внецентренного сжатого стержня, согласно принципу независимости действия равны алгебраической сумме напряжений от каждого внутреннего силового фактора:

(2)

где

После несложных преобразований в окончательном виде формула для вычисления нормальных напряжений при внецентренном сжатии имеет следующий вид

(3)

где - радиусы инерции поперечного сечения стержня (см);

- координаты точки поперечного сечения, в которой вычисляются нормальные напряжения (см);

А – площадь поперечного стержня (см²);

- моменты инерции стержня (см⁴).

Формула (3) позволяет определять напряжения в любом волокне стержня. Выражение в скобках показывает во сколько раз возрастает нормальное напряжение в стержне в результате внецентренного приложения нагрузки.

Наиболее напряженными волокнами являются волокна, в которых суммируются напряжения сжатия от всех трех силовых факторов.

В рассматриваемом стержне прямоугольного сечения максимальные по абсолютному значению напряжения возникают в волокне, которое проходит через точку 1 (рис. 2).

Иными словами максимальные нормальные напряжения при внецентренном сжатии возникают в точках наиболее удаленных от нейтральной линии. По этому для определения опасных точек необходимо предварительно определить положение нейтральной линии.

Рис. 2

Так как на нейтральной линии нормальные напряжения равны нулю уравнение нейтральной линии получим изходя из выражения (3) приравняв его к нулю.

(4)

Выражение (4) нетрудно привести к прямой в отрезках из которого определяются значения которые отсекает нейтральная линия на координатных осях.

На оси Z: отсекается отрезками ; на оси y: ― (5)

Из выражений (5) следует:

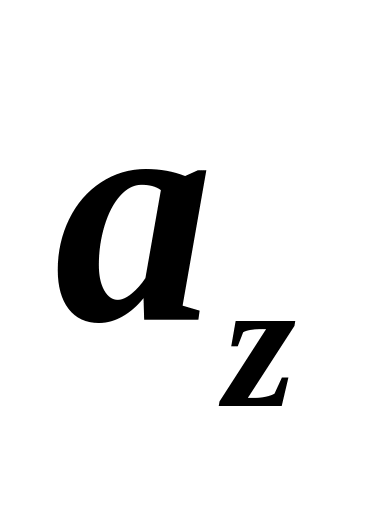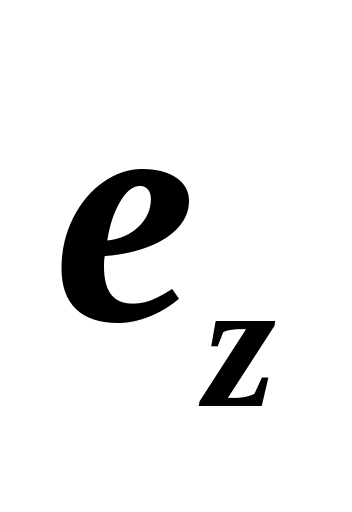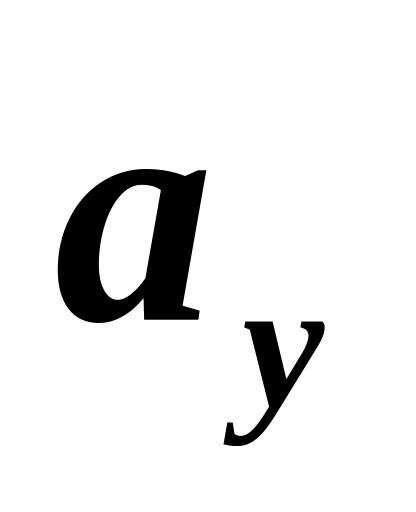1. Так как в формулу отрезков входит знак «минус», то и , и 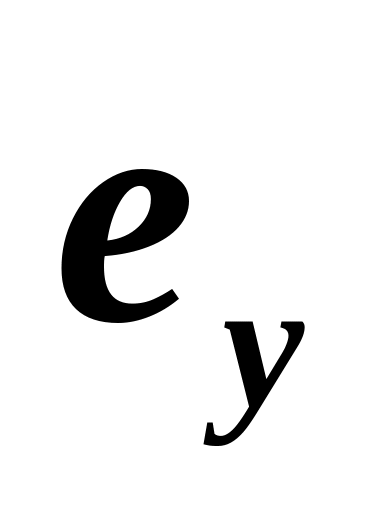всегда имеют разные знаки, а это значит, что полюс и нейтральная линия всегда лежат по разные стороны относительно центра тяжести сечения.

2. При удалении полюса от центра тяжести ( и увеличиваются) нейтральная линия приближается к нему ( и уменьшаются) и наоборот.

3. Положение нейтральной линии не зависит от величины действующей нагрузки.

Прочность стержня обеспечена, если максимальные напряжения не превышают расчетное сопротивление материала т. е.:

(6)

где --координаты точек наиболее удаленных от нейтральной линии.

Из условия прочности (6) нетрудно получить формулу для определения допускаемой нагрузки:

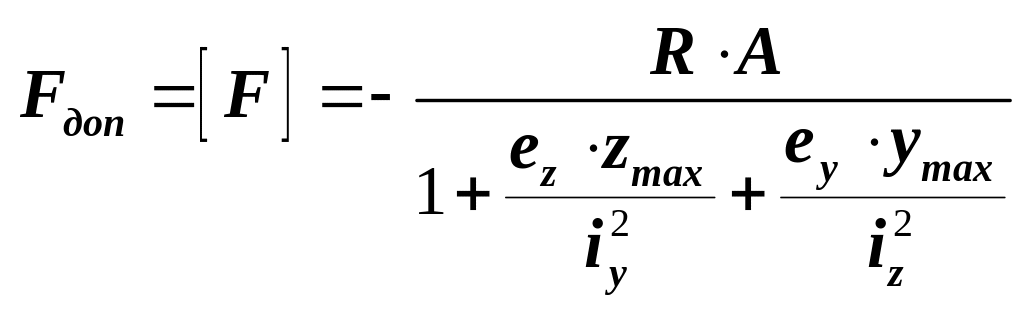(7)