Пример №1

Расчет тонкостенного стержня открытого профиля.

Для заданного стержня необходимо:

- определить положение центра тяжести;

- вычислить главные центральные моменты инерции;

- построить эпюру секториальной площади (полюс помещаем в центр тяжести сечения);

- вычислить секториально-линейный статический момент;

- построить эпюру главной секториальной площади (полюс помещаем в центр изгиба);

- вычислить секториальный момент инерции;

- вычислить момент инерции при чистом кручении;

- вычислить изгибно-крутильную характеристику;

- записать дифференциальное уравнение углов закручивания и граничные условия;

- вычислить внутренние усилия в стержне и построить эпюры (стержень разбить на 4 участка);

- вычислить нормальные напряжения в опасном сечении и построить эпюры.

Характеристики материала:

Схема сечения №1; точка приложения силы 2;

Рис. 5

Решение

1. Разбиваем фигуру на простейшие, определяем площади прямоугольников.

2. Определяем положение центра тяжести сечения относительно осей

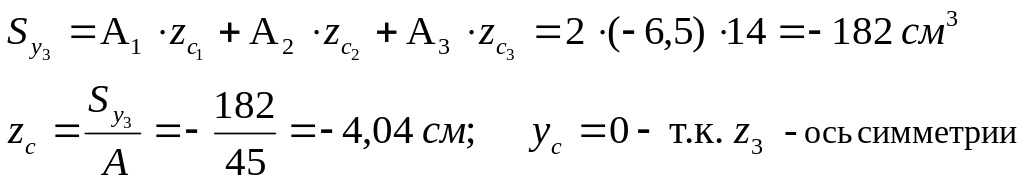
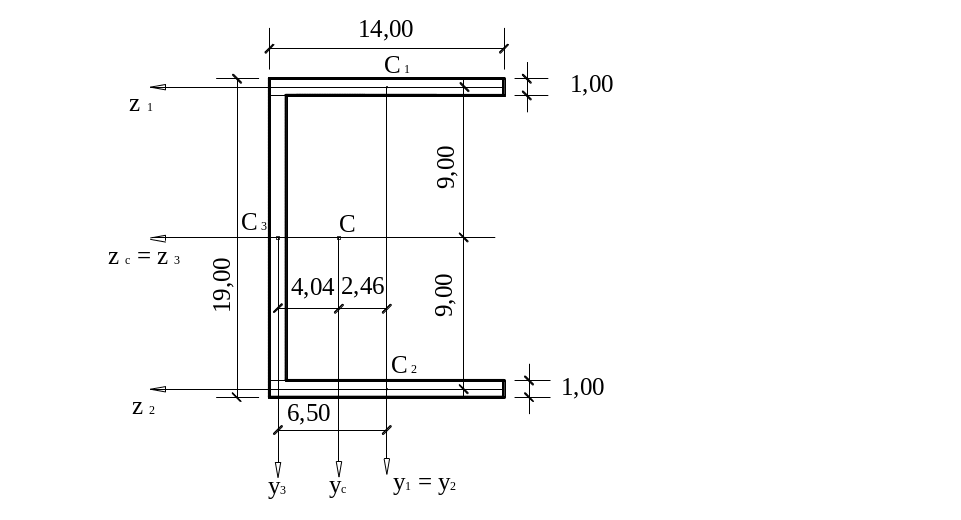Рис. 6

3. Вычисляем главные центральные моменты инерции

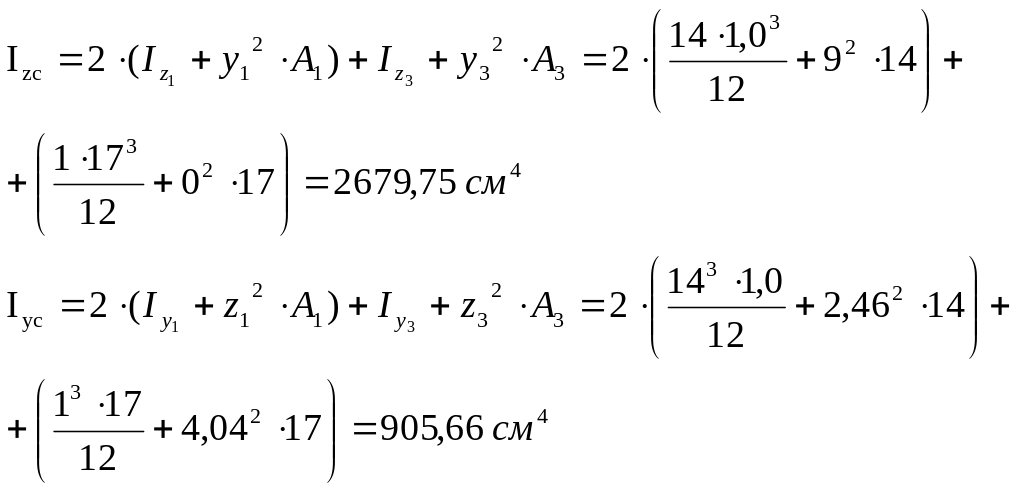
4. Вычисляем секториальную площадь.

Заменяем швеллер расчётной схемой, совпадающей с осевыми линиями сечения. Строим эпюры координат z и y.

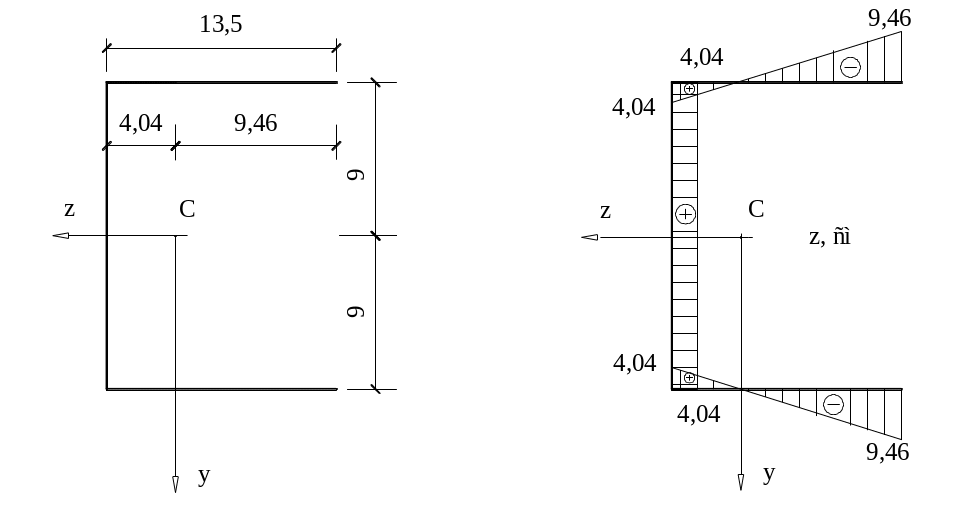Рис. 7 Рис. 8

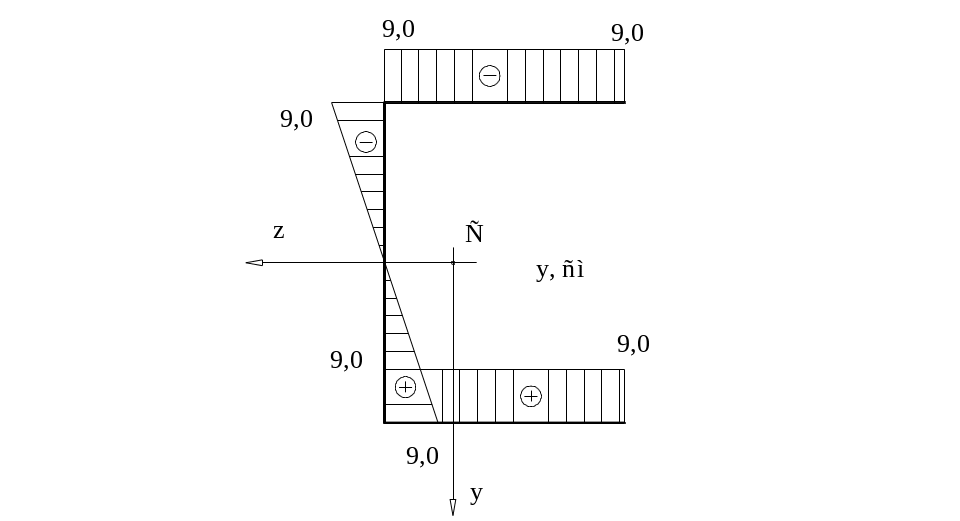Рис. 9

Строим эпюру секториальной площади (полюс выбираем в центре тяжести сечения P = C). 0 – начало отсчета секториальной площади (на пересечении контура и оси симметрии).

,

где – координаты точки начала элемента;

– координаты точки конца элемента.

z y

Координаты 1 ( 4,04 ; 9 )

точек 2 ( -9,46 ; 9 )

относительно 3 ( 4,04 ; -9 )

центра 4 ( -9,46 ;-9 )

тяжести 0 ( 4,04 ; 0 )

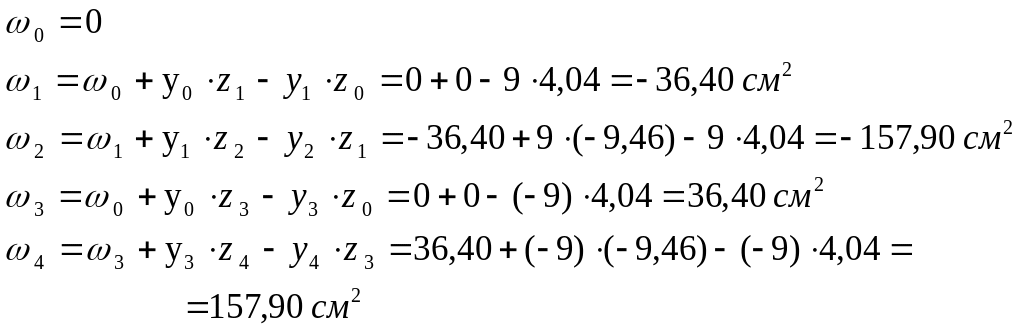
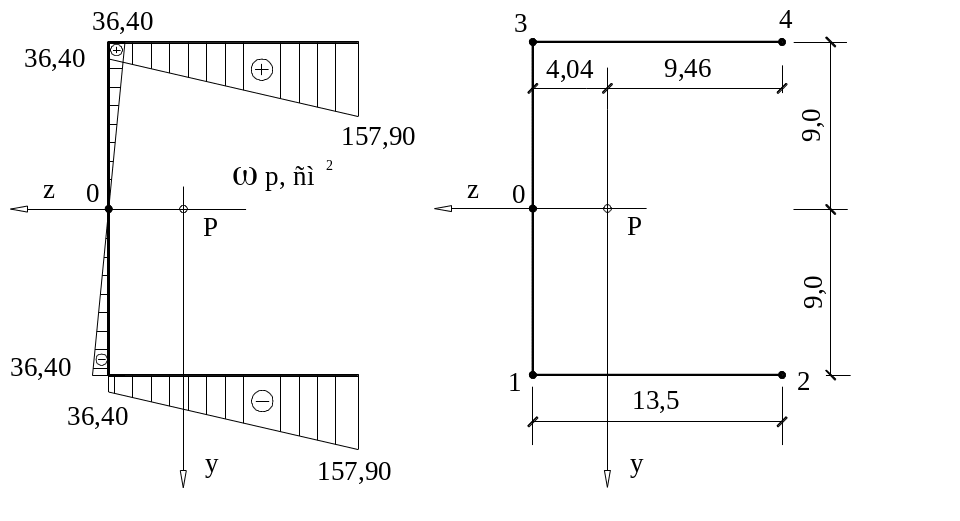Рис. 10 Рис. 11

5. Определяем положения центра изгиба.

Сначала вычисляем секториально-линейные статические моменты, для этого умножаем эпюру на соответствующие эпюры координат (по способу Верещагина).

(при умножении симметричной эпюры на кососимметричную результат равен 0).

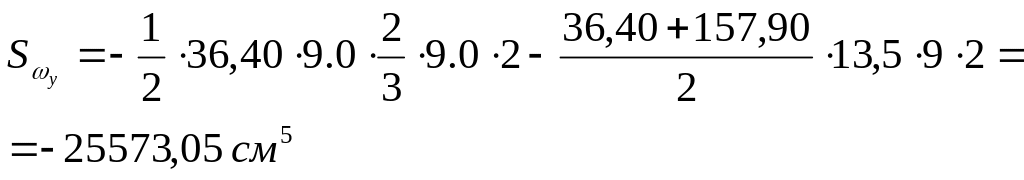
Определяем положения центра изгиба.

6. Строим эпюру главной секториальной площади (полюс помещаем в центр изгиба P = D). 0 – начало отсчета секториальной площади (на пересечении контура и оси симметрии).

z y

Координаты 1 ( -5,5; 9 )

точек 2 ( -19 ; 9 )

относительно 3 ( -5,5;-9 )

центра 4 (-19,0;-9)

изгиба 0 ( -5,5; 0 )

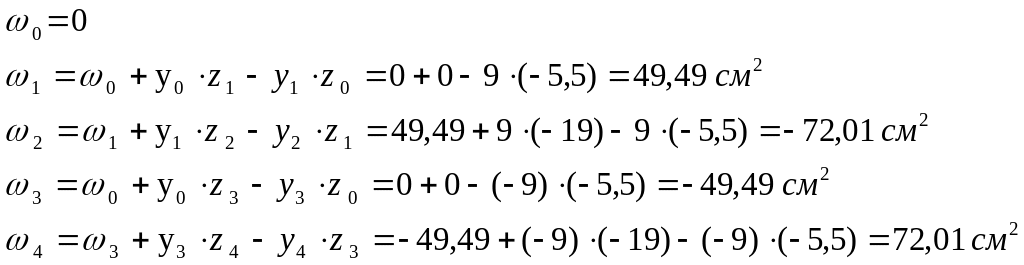
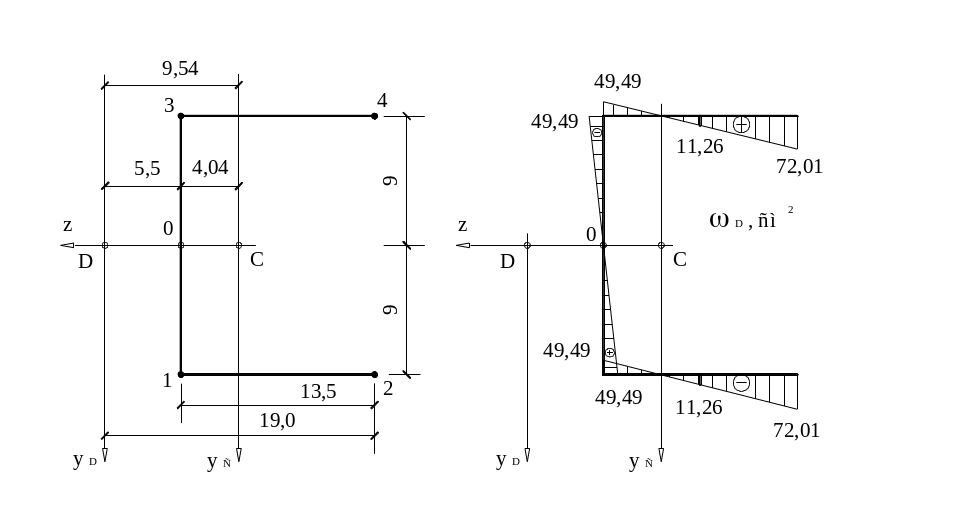
Рис. 12 Рис. 13

0 – главная секториальная нулевая точка – ближайшая к центру изгиба нулевая точка, у сечений с одной осью симметрии она расположена на пересечении контура и этой оси.

7. Вычисляем секториальный момент инерции .

Для этого перемножаем эпюру на эпюру . (по способу Вере-

щагина и формуле Симпсона).

8. Вычислим момент инерции при чистом кручении

, где

– меньший размер,

– размер по осям,

- для швеллера.

9. Вычислим изгибно-крутильную характеристику

Предварительно вычислим модуль сдвига:

Изгибно-крутильная характеристика:

10. Дифференциальное уравнение углов закручивания

, или

, где

– угол закручивания,

– интенсивность внешней распределённой крутящей нагрузки с учётом знака (знак «плюс» когда нагрузка стремится вращать против часовой стрелки при взгляде с положительного направления оси х )

Решение уравнения:

Произвольные постоянные зависят от граничных условий

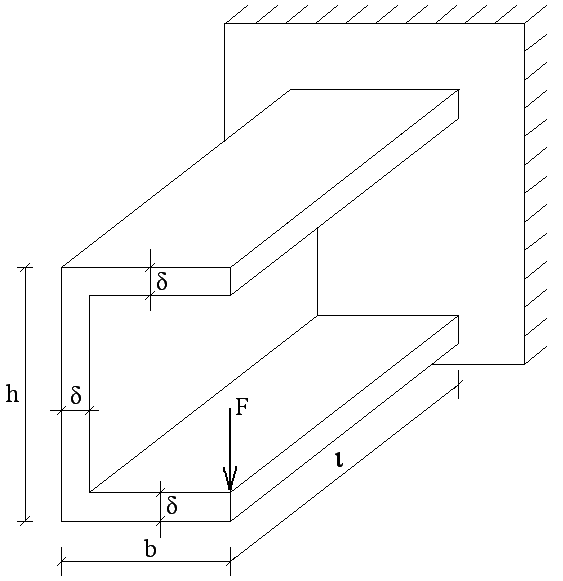
_{Рис. 14}

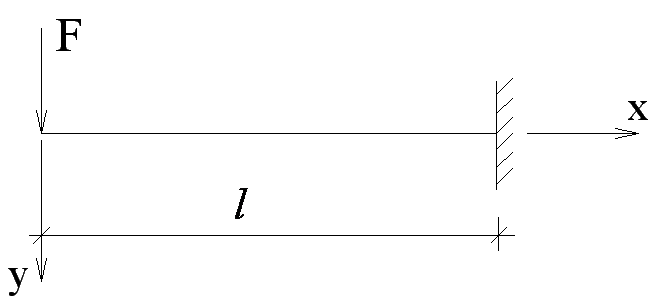
Запишем граничные условия

Для свободного торца ( )

или

Для защемленного торца ( )