Лекция 6. Осевое растяжение-сжатие стержней. Определение напряжений, деформаций и перемещений. Расчёты на прочность и жёсткость.

Осевое или центральное растяжение (сжатие) относят к простым видам сопротивления. Название этого вида деформации обусловлено тем, что линия действия сил (равнодействующей сил), приложенных к стержню, совпадает с осью стержня (ось стержня проходит через центры тяжести поперечных сечений).

Продольное внутреннее усилие (N) будет положительным при растяжении элемента и отрицательным в случае сжатия.

Продольное внутреннее усилие (N) в любом сечении равно алгебраической сумме проекций всех внешних сил (включая опорные реакции), взятых по одну сторону от сечения, на продольную ось стержня.

Напряжения в поперечных сечениях характеризуют интенсивность внутренних сил в поперечном сечении.

Соотношение (6.1) позволяет вычислить среднее напряжение по площади поперечного сечения. Бернулли были предложены допущения – гипотезы плоских сечений: поперечные сечения, плоские до нагружения остаются плоскими и перпендикулярными продольной оси и после нагружения. В силу принятых гипотез σ_y=σ_z=τ_yx=τ_yz=0, σ_x≠0, поэтому напряженное состояние в элементе объёма – линейное (только одно из главных напряжений отлично от нуля), рис. 6.1. Нормальное напряжение в поперечном сечении при данном виде деформации является функцией от продольного внутреннего усилия N_x и зависит от геометрической характеристики поперечного сечения – площади А. Определяют напряжение по формуле

σ=σ_x=N_x/A. (6.2)

Знак у напряжения определяется знаком продольной силы.

Рис. 6.1. Схема деформации элементарного параллелепипеда при одноосном растяжении

При растяжении (сжатии) различают абсолютные ∆l и относительные ε деформации. Абсолютная деформация – это разница между длиной стержня до и после деформации, т.е. та величина, на которую он изменил свою длину ∆l=/l₁-l/. Относительная деформация – это, как ясно из названия, отношение абсолютной деформации к первоначальной длине стержня ε=∆l/l.

Деформации элементов конструкций, материал которых работает в упругой стадии, определяются на основании закона Гука, записанного в случае одноосного (линейного) напряжённого состояния в следующем виде:

(6.3)

Закон Гука (6.3) устанавливает прямопропорциональную зависимость между действующим в рассматриваемой точке нормальным напряжением и относительной линейной деформацией материала (по направлению ). Коэффициент пропорциональности Е носит название модуля упругости первого рода (модуля продольной упругости, модуля Юнга) и имеет размерность напряжения.

При одноосном растяжении (сжатии) кроме продольной деформации возникают также деформации и в поперечных направлениях, противоположные по знаку деформации (рис. 6.1). Отношение деформации к или к , взятое по абсолютной величине, называется коэффициентом Пуассона (коэффициентом поперечной деформации) ν.

Для изотропных материалов

(6.4)

Коэффициент Пуассона для различных материалов может принимать значения от 0 до 0,5 (для стали обычно = 0,24… …0,33, для алюминиевого сплава – 0,3).

Модуль упругости первого рода и коэффициент Пуассона являются основными характеристиками упругих свойств материала. Они определяются экспериментальным путем. Наиболее просто в техническом отношении осуществляется опыт, в котором Е и определяются по результатам испытания образца на осевое растяжение.

Перемещения сечений происходят в результате деформирования стержня. Перемещения, соответствующие удлинению считаются положительными. Перемещения, вызванные внешними силовыми факторами, определяют с помощью зависимости (6.5).

. (6.5)

В случае, когда в пределах грузового участка внутреннее усилие и жёсткость стержня постоянны, это выражение принимает вид

Перемещения, вызванные изменением температуры, определяются с помощью зависимости

Расчет на прочность и жесткость при осевом растяжении (сжатии).

Для расчета на прочность пользуются условием прочности, которое при данном виде сопротивления имеет вид:

(6.8)

В этих выражениях , , 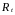- расчетные сопротивления по нормальным напряжениям для хрупкого и пластичного материала соответственно. Максимальное значение напряжения определяют с помощью эпюры напряжений, полученной через отношения N_x/A.

В расчете на жесткость применяют условия жесткости:

. (6.9)

Первое условие для полного перемещения стержня, а второе - для максимального перемещения сечения. В квадратных скобках приведены допустимые значения. Для определения опасного сечения, в котором возникает , строят эпюру перемещений.

Пример построения эпюр.