Розділ 2 Аналітична геометрія

2.1. Вектори, типи добутків векторів та методи їх розв’язування.

До лінійних належать такі операції над векторами:

• множення вектора на скаляр . При цьому одержаний век­тор геометрично, залежно від величини і знака , розтягується, стискається, змінює напрям ;

• додавання векторів. Дія виконується за правилом паралело- грама або трикутника.

Якщо вектор задано в координатній формі, то у разі множення його на скаляр всі координати треба помножити на цей скаляр, а в разі додавання — додати відповідні його координати.

Cкалярного добутку векторів: ;

,

Кут  між векторами: ,

умови паралельності та перпендикулярності двох векторів.

За використання векторного добутку слід пам’ятати, що він некомутативний, а його модуль дорівнює площі паралелограма, побудованого на векторах-множниках. Знаходять векторний добуток за формулою:

.

Геометричний зміст мішаного добутку полягає в тому, що його модуль дорівнює об’єму паралелепіпеда, побудованого на векторах добутку.

.

У зв’язку з цим його часто використовують для знаходження об’єму і перевірки компланарності трьох векторів

Приклад 1.

Обчислити довжини діагоналей паралелограма, побудованого на векторах і , якщо відомо, що .

Розвязок.

З визначення операції додавання векторів відомо, що одна діагональ паралелограма ,а друга . Довжина довільного вектора визначається за формулою: . Тоді:

Приклад 2.

 Дано три послідовні вершини паралелограма: . Знайти його четверту вершину і кут між діагоналями.

Розвязок.

Нехай шукана вершина має координати . З умови колінеарності векторів і маємо: , або . Згідно з властивостями паралелограма або . Діагоналі паралелограма дорівнюють відповідно сумі і різниці векторів-сторін ; . Кут між діагоналями знайдемо за формулою:

соs   отже, .

Приклад 3.

Знайти площу паралелограма, діагоналями якого є вектори і , де і — одиничні вектори, а кут між ними дорівнює 45.

Розвязок.

Позначимо через сторони паралелограма, тоді , звідки . Площу паралелограма знайдемо як модуль векторного добутку . Отже, .

Приклад 4.

Знайти площу і висоту трикутника, вершинами якого є: _{Розвязок}

Знайдемо вектори і . Модуль їх векторного добутку буде дорівнювати подвоєній площі трикутника: звідки .

Знайдемо висоту трикутника: .

Приклад 5.

Для піраміди з вершинами , обчислити об’єм, площу грані АВС і висоту, опущену на цю грань.

Розвязок.

Знайдемо вектори . Модуль мішаного добутку у шість разів більший за об’єм піраміди, побудованої на векторах , тобто Для обчислення площі гра- ні АВС знайдемо 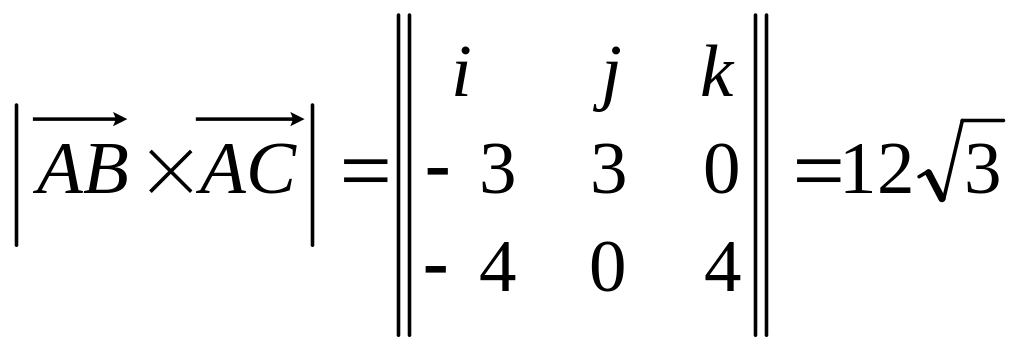. Тоді , а висота піраміди .

2.2 Пряма на площині

Пряма лінія на площині ХОУ - множника точок М (х;у), що задовольняють рівняння , де А, В, D – задані коефіцієнти прямої, причому

Рівняння прямої, що проходить через точку Мо (х_о; у_о) і має вектор нормалі має вигляд:

А(х—х_о)+В(у—у_о) = 0 (1)

Рівняння прямої, що проходить через дві різні точки М₁(х₁;у₁) i М₂(х₂;y₂) таке:

(2)

Piвняння прямої, що проходить через данy точку М₀(х_о;у_о) y зaданомy напрямку

y - y_o = k(x—x_o) (3)

де k = tgα — кутовий коефіцієнт прямої, α — кут між прямою i віссю ОХ.

Якщо прямої i задані рівняннями з кутовим коефіцієнтами і , то кут між ними обчиcлюється по формулі:

Умова паралельності прямих i має вид k₁ = k₂ , a yмoвa їх перпендикулярності Якщо прямі ₁ і ₂ задані загальними рівняннями A₁х+ В₁y+C₁ =0 і A ₂x+В₂y+C₂=0 , то величина кута між ними обчислюється по формyлі

умова їх паралельності

умова їх перпендикулярності A₁A₂+B₁B₂=0.

Відстань d від точки M₀(x_0;y₀) до прямої A_x+B_y+C=0 обчислюється по формулі

Приклад 1.

Дано трикутник із вершинами A(1,-2), В(5;4) i С(-2;0). Скласти рівняння медіани СМ, висоти BN та бісектриси AP.

Разв'язок. Якщо М(х₁;у₁) — середина сторони АB, то і звідси М(3;1).

Тeпер рівняння медіани CM знайдемо як рівняння прямої, що проходить через дві точки С(-2;0) i М(3;1). Маємо за формулою (2):

Оскільки висoта BN проходить через точку B i має вектор нормaлі то за формулою (1) дістанемо рівняння прямої BN:

- 3(х- 5) + 2(y-4)=0 aбo Зх-2y-7=0.

Для визначення рівняння прямої AP скористаємося властивістю бісектриси :

Маємо тому

.

Оскільки точка P(x;y) ділить відрізок ВС y відношенні то за формулами , дістанемо і тоді,

Отже, рівняння бісектриси AP, знайдемо як рівняння прямої, що проходить

через дві точки A(1;-2) i (формула 2).

Маємо

або або

Завдання4

Знайти рівняння висоти, медіани i бісектриси тpикутника зі сторонами