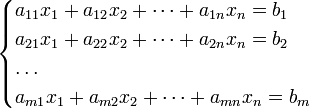Вопросы к коллоквиуму (I часть)

1. Матрицы. Виды матриц. Действия над матрицами.

2. Определитель квадратной матрицы. Формулы вычисления определителя n-го порядка. Теорема Лапласа.

3. Определитель квадратной матрицы. Свойства определителя.

4. Обратная матрица. Теорема о существовании обратной матрицы.

5. Ранг матрицы. Методы вычисления ранга матрицы.

6. Базисный минор. Теорема о базисном миноре.

7. Системы линейных уравнений. Решение СЛАУ. Виды СЛАУ. Матричная запись СЛАУ. Решение СЛАУ методом обратной матрицы.

8. Системы линейных уравнений. Теорема Крамера.

9. Системы линейных уравнений. Решение СЛАУ методом Гаусса.

10. Системы линейных уравнений. Теорема Кронекера – Капелли. Схема решения СЛАУ.

11. Системы линейных однородных уравнений. Фундаментальная система решений.

12. Комплексные числа. Различные формы комплексного числа. Действия над комплексными числами.

13. Комплексные числа. Вывод формулы Муавра для возведения в степень комплексного числа. Формула извлечения корня n-ой степени из комплексного числа.

Вопрос №1

Матрица — это прямоугольная таблица размером m - строк на n – столбцов, элементами которой являются числа или буквенные выражения

Виды матрицы

• Квадратная (число строк=числу столбцов)

• Диагональная (все элементы кроме главной диагонали=0)

• Единичная (элементы главной диагонали=1, а остальные элементы=0)

• Нулевая (все элементы=0)

• Треугольная (элементы расположенные по одну сторону гл.диагонали= 0)

• Ступенчатая (крайний элемент каждой строки находится правее предыдущей строки)

Операции над матрицами

• Сложение матриц (А+В=С, каждый элемент матрицы С равен с_ij=а_ij+b_ij)

• Умножение матрицы на число (А×λ=С того же размера что и матрица А, причем элементы матрицы С находятся по формуле с_ij=λ×а_ij)

• Умножение матриц (А*В=С элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго)

• Т 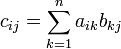ранспонирование (строки заменяем столбцами)

Вопрос №2,№3

Определителем матрицы называют число характеризующее квадратную матрицу.

• Определителем 1 порядка называют само это число

• Определителем 2 порядка называют число = главная диагональ - побочная диагональ)

• Определителем 3 порядка называю число, вычисляемое по правилу треугольника или Саррюса

• Определителем n – порядка называют число равное алгебраической сумме n! членов, каждое из которых является произведением n элементов матрицы взятых по одному элементу каждой строки и каждого столбца

Алгебраическое дополнение=(-1)^i+j × M_ij

Минор (M) — определитель матрицы (n-1) порядка, полученное при вычеркивании i - строки и j - столбца.

Теорема Лапласа — определитель n - порядка равен сумме произведения любой строки(столбца) на их алгебраическое дополнение.

Свойства определителя

• Если все элементы некоторой строки=0, то определитель=0

• Если 2 строки определителя поменять местами, то определитель изменит свой знак на противоположный, величина не изменится.

• Если все элементы некоторой строки определителя умножить на число (отличное от 0), то определитель тоже умножится на это число.

• Если определитель содержит 2 одинаковые строки, то он=0

• Сумма произведения элементов какой либо строки определителя, на соответствующее алгебраическое дополнение другой строки, то определитель=0

• Определитель не изменится если к элементам некоторой строки прибавить элементы другой строки предварительно умноженное на число

• Определитель произведения 2 квадратных матриц=произведению определителя этих квадратных матриц

• Если некоторая строка представляет собой сумму А+В, то определитель=сумме определителей один из которых содержит только элементы с индексом А, а другой только элементы с индексом В

Вопрос №4

Обратная матрица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

А×А^-1=А^-1×А=Е

Теорема о существовании обратной матрицы.

Обратная матрица А-1 существует тогда, и только тогда, когда исходная матрица невырожденная(определитель не равен 0)

Вопрос №5

Ранг матрицы — наивысший порядок минора, отличного от 0

Методы вычисления ранговой матрицы.

• Перебор минора (переборе всех миноров матрицы и нахождения высшего порядка минора, отличного от 0)

• Метод окаймляющих миноров

• Метод элементарных преобразований(приведение матрицы с помощью элементарных преобразований к ступенчатому виду)

Вопрос №6

Минор k – порядка называется базисным, если он отличен от 0, а все миноры k+1=0 либо не существует, у ненулевой матрицы базисных миноров бесконечное множество.

Теорема о базисном миноре.

• Базисные строки(столбцы) матрицы линейно независимы

• Любая строка (столбец) матрицы есть линейная комбинация базисных строк (столбцов)

Вопрос №7

Система линейных алгебраических уравнений(СЛАУ) называют систему m – уравнений с n – неизвестных, имеющая вид