7. Монотонные последовательности. Признак сходимости монотонных последовательностей.

Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Последовательность   элементов множества   называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.

 — неубывающая 

Последовательность   элементов множества   называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.

 — невозрастающая 

Последовательность   элементов множества   называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.

 — возрастающая 

Последовательность   элементов множества   называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.

• — убывающая 

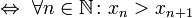
Если монотонная последовательность   ограничена, то она сходится.

Доказательство. Так как последовательность   ограничена, то множество ее элементов имеет точные верхнюю   и нижнюю   грани. Пусть   – неубывающая последовательность и  – точная верхняя грань множества ее элементов. Это означает, что для любого числа   можно указать такой элемент  , что   и  . Эти два неравенства равносильны неравенству   или  . Так как   – неубывающая последовательность, то при   выполняется   или  . Это означает, что при   выполняется   или  . Таким образом,  . Аналогично доказывается случай, когда   – невозрастающая последовательность.

Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме сходящаяся монотонная последовательность ограничена.

Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность   сходится к числу ноль, но не является монотонной.

Замечание 3. Если последовательность   неубывающая сходящаяся и  - ее предел, то для всех номеров n выполняется неравенство  . Аналогично, если   невозрастающая сходящаяся последовательность и   – ее предел, то для всех номеров n справедливо  .

8. Лемма о вложенных отрезках.

Определение 1. Множество, элементами которого являются отрезки, называется системой отрезков.

Определение 2. Система замкнутых отрезков   называется стягивающей, если

1.  , т.е. каждый последующий отрезок расположен внутри предыдущего;

2.  , т.е. длины отрезков стремятся к нулю.

Лемма о вложенных отрезках:

Для любой системы замкнутых стягивающихся отрезков существует единственная точка, принадлежащая всем отрезкам.

Доказательство.

1. Рассмотрим множество   левых концов наших отрезков. Очевидно, что

а) 

б)

Поэтому, по предыдущей теореме, существует конечный  .

2. Рассмотрим множество   правых концов наших отрезков. Очевидно, что

а) 

б) 

поэтому существует конечный  .

3. Так как по условию  , то 

.

Обозначим этот общий предел через c:

.

4. Так как   а  , то очевидно что  , т.е. точка    ; (она принадлежит всем отрезкам сразу).

5. Докажем, что точка c единственная. Предположим противное, что   точка  , такая что    . Но тогда было бы, что  что противоречит тому, что  .

Отметим одну деталь: мы доказали не только существование точки c, принадлежащей всем отрезкам, но и то, что 

9. Предел последовательности (1+x/n)ⁿ=X_э-1

10. Частичные последовательности. Теорема о пределе последовательности сходящейся последовательности.

11. Лемма Больцано-Вайерштрасса

Лемма Больцано - Вейерштрасса. Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.

Доказательство. При доказательстве этой леммы использован широко применяемый прием - “деление отрезка пополам”.

Итак, пусть некоторая последовательность   ограниченна, т.е.  . Это означает, что все члены   последовательности   лежат на отрезке  .

1. Построение стягивающей системы отрезков.

Разделим отрезок   пополам точкой  . Мы получим два отрезка   и  . Так как на все отрезке   имеется бесконечно много членов последовательности, то хотя бы на одной половине также будет бесконечно много членов последовательности. Оставим для дальнейшего рассмотрения эту половину (если на обеих половинах бесконечно много членов последовательности - оставим любую из них) и назовем ее отрезком  .

Разделим отрезок   пополам. Мы получим два отрезка   и  . Так как на всем отрезке   находиться бесконечно много членов последовательности, то хотя бы на одной половине также находится бесконечно много членов последовательности. Оставим для дальнейшего рассмотрения эту половину и назовем ее отрезком  .

Разделим отрезок   пополам. Так как на всем отрезке   находиться бесконечно много членов последовательности, то ....

Продолжим эту процедуру до бесконечности. В результате мы получим систему отрезков  ,  ,  ,  , которые характеризуются тем, что

а) на каждом из них имеется бесконечно много членов последовательности;

б) 

в)  .

По лемме о вложенных отрезках отсюда следует, что 

2. Выделение подпоследовательности

Рассмотрим отрезок   и возьмем любой член последовательности  .

Рассмотрим отрезок   и возьмем любой член последовательности  . Так как на   бесконечно много членов  , то всегда можно выбрать  .

Рассмотрим отрезок   и возьмем любой член последовательности  . Так как на   бесконечно много членов  , то всегда можно выбрать  .

Рассмотрим отрезок   и возьмем  .

Продолжая эту процедуру до бесконечности получим подпоследовательность   такую, что .

3. Сходимость получившейся подпоследовательности

Так как   и   то по теореме “о двух милиционерах” 

12. Критерий сходимости последовательности Коши.

Определение. Подпоследовательность   называется последовательностью Коши или фундаментальной, если 

Теорема ( Критерий Коши ). Для того, чтобы последовательность   сходилась, необходимо и достаточно чтобы она была фундаментальной.

Доказательство:

Необходимость. Пусть   сходится. 

Достаточность. Пусть   - фундаментальная последовательность. Докажем, что она ограничена и  .

Так как последовательность фундаментальна, то  , в  -окрестности которой существуют все элементы  .

Предположим,  .

В отрезке [A, -A] содержатся все элементы последовательности, т.е.   - ограниченна.

В следствие теоремы Больцано-Вейерштрасса ( ) < ( ).

 в силу произвольности