1. Понятие последовательности. Предел последовательности.

Если каждому числу n натурального ряда чисел 1, 2, …, n, ставится в соответствие по определенному закону некоторое вещественное число x_n, то множество занумерованных вещественных чисел x_1, x_2, x_3, x_n, мы и будем называть числовой последовательностью.

Число   называется пределом числовой последовательности  , если последовательность   является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

2. А) Свойства сходящихся последовательностей: единственность предела. Б) Ограниченность последовательности. В) Теоремы о пределах, связанных с неравенствами о предельном переходе в неравенстве. Г) Теорема о зажатой переменной

А) Определение: Если последовательность a_n имеет предел, то этот предел единственный.

Доказательство (от противного): Допустим, что этот предел не единственный, т.е. существует 2-а предела последовательности, отличных друг от друга: lim_(n->∞) a_n = в₁ ; lim_(n->∞) a_n = в2 ; в1≠в2. Рассмотрим число А = (в1 + в2)/2 (рисунок на прямой со стрелочкой взят отрезок в1в2 и А - середина отрезка) В1 < A, тогда найдётся номер №1 ; A(наоб-т)n > №1 : a_n < A (по свойству если дана последовательность a_n lim_(n->∞) a_n = в, в>α, то начиная с некоторого номера все члены будут меньше α). в2>A, тогда найдётся номер №2, такой что для любого n > №2 выполняется неравенство: a_n > A. Пусть № = max {№1 ; №2}, и для любого n > №, выполняются оба неравенства одновременно, следовательно, для любого члена любого члена последовательности выполняется неравенство: A < a_n < A, а это противоречие.

Б) Последовательность {x_n} называется ограниченной снизу (сверху), если существует такое число C, что все члены последовательности удовлетворяют условию x_n ≥ C (x_n ≤ C). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной.

В) Теорема: если элементы сходящейся последовательности {x_n}, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

Доказательство. Пусть все элементы x_n, по крайней мере, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {x_n}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |x_n - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < x_n - a < b - a. Используя правое из этих неравенств, получим x_n < b, а это противоречит условию теоремы. Случай x_n ≤ b рассматривается аналогично. Теорема доказана.

Следствие 1. Если элементы x_n и y_n сходящихся последовательностей {x_n} и {y_n}, начиная с некоторого номера, удовлетворяют неравенству x_n ≤ y_n, то их пределы удовлетворяют такому же неравенству:

В самом деле, элементы последовательности {y_n - x_n} неотрицательны, а поэтому неотрицателен и ее предел  . Отсюда следует, что

  

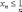
Следствие 2. Если все элементы сходящейся последовательности {xn} находятся на сегменте [a, b], то и ее предел c также находится на этом сегменте.

В самом деле, так как a ≤ xn ≤ b, то a ≤ c ≤ b.

Следующая теорема играет важную роль в различных приложениях.

Теорема. Пусть {x_n} и {z_n} - сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {y_n} удовлетворяют неравенствам x_n ≤ y_n ≤ z_n. Тогда последовательность {y_n} сходится и имеет предел a.

Доказательство. Нам достаточно доказать, что последовательность {y_n - a} является бесконечно малой. Обозначим через N* номер, начиная с которого выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполняться также неравенства x_n - a ≤ y_n - a ≤ z_n - a. Отсюда следует, что при n ≥ N*элементы последовательности {y_n - a} удовлетворяют неравенству≤

|y_n - a| ≤ max {|x_n - a|, |z_n - a|}.

Так как   и  , то для любого ε > 0 можно указать номера N1 и N2 такие, что при n ≥ N1 |x_n - a| < ε, а при n ≥ N2 |z_n - a| < ε. Пусть N = max{N*, N1, N2}. Начиная с этого номера, имеет место неравенство |y_n - a| < ε. Итак, последовательность {y_n - a} - бесконечно малая. Теорема доказана.

Г) Теорема о зажатой переменной. Пусть даны три последовательности {xn},{уn} и {zn}, причѐм, начиная с некоторого n выполняется неравенство

x_n≤у_n≤z_n.

Пусть последовательности {x_n} и {z_n} имеют один и тот же конечный

или бесконечный определѐнного знака предел Θ. Тогда последовательность {у_n}

также имеет предел равный Θ. Доказательство проведѐм для случая, когда предел конечен.

Доказательство. Пусть неравенство из условия теоремы выполняется при

n>n₁: x_n≤у_n≤z_n.

Обозначим предел последовательностей

{x_n} и {z_n} через А. Возьмѐм Σ > 0.

При n > n₂:| x_n- А |< Σ или А-Σ≤x_n≤А+Σ.

При n > n₃: |z_n-А|< Σ или А-Σ ≤ z_n ≤ А+Σ.

При n > max (n₁, n₂, n₃) имеют место все три написанные двойные неравенства. Нам нужны обведѐнные их части.

А - Σ ≤ xn ≤ уn ≤ zn ≤ А + Σ ,

то есть,

А - Σ ≤ у_n ≤ А + Σ или | у_n - А | < Σ,

а это означает, что у_n → А.