3. Бесконечно малые последовательности. Связь б.М. С пределом последовательности свойства б.М. (сумма и произведение)

Определение 1. Последовательность   называется бесконечно-малой последовательностью, если  , т.е. если .

Определение 2. Последовательность   называется бесконечно-большой последовательностью, если   (это записывается еще и так:  , не учитывая знака перед  ), т.е. если

.

Сумма и разность бесконечно-малых последовательностей есть также бесконечно-малая последовательность.

Доказательство:

 _{- б.м.п.} =>

 _{- б.м.п.} =>

Возьмем . Тогда

откуда следует, что  есть б.м.п.

Следствие. Сумма любого конечного числа б.м.п. ест также б.м.п

Произведение б.м.п на ограниченную последовательность есть б.м.п.

Доказательство:

 - ограничена. =>

 - б.м.п. =>

.

Но тогда 

отсюда и следует, что   есть б.м.п.

3. Б.м.п. ограничена

Доказательство:

Пусть   - б.м.п. Тогда  .

Возьмем  .

Тогда   т.е.   ограничена.

Следствие. Произведение б.м.п. есть также б.м.п.

4. Пусть   - б.м.п. и  . Тогда   есть б.б.п.

Доказательство:

 - б.м.п =>  .

Возьмем любое   и положим  .

Тогда 

отсюда следует, что   есть б.б.п.

5. Пусть   - б.б..п, тогда   есть б.м.п.

 - б.б.п =>  .

Возьмем любое   и положим 

Тогда 

отсюда следует, что   есть б.м.п.

4. Бесконечно большая последовательность. Связь б.м. с б.б.

Последовательность     называется бесконечно большой (б.б.), если абсолютные величины всех ее элементов – начиная с некоторого номера  N  – превышают любое сколь угодно большое наперед заданное число  E > 0. Другими словами,      при  n > N.        Легко показать, что общий член     бесконечно большой последовательности может быть представлен в виде

где     – некоторая бесконечно малая последовательность.

 Теорема 1. Если {х_n} — бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность

бесконечно малая, и, обратно, если {α_n} — бесконечно малая последовательность и все её члены отличны от нуля {α_n} ≠ 0, то последовательность { 1 / α_n } – бесконечно большая.   Доказательство. Пусть { х_n} — бесконечно большая последовательность. Возьмем любое как угодно малое положительное число ε > 0 и положим

Согласно определению для этого существует такой номер N , что при n > N будет | x_n | > A. Отсюда получаем, что

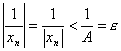
для всех n > N. А это значит, что последовательность

бесконечно малая.

5. Теорема об арифметических операциях над пределами последовательностей. Неопределенности.

Пусть А и В — произвольные множества; их суммой, или объединением С = А ∪ В, называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В.

Аналогично определяется сумма любого конечного

числа множеств. Если A_k (k =1, n) — произвольные

множества, то их сумма A_kkn=1

∪ есть совокупность эле-

ментов, каждый из которых принадлежит хотя бы од-

ному из множеств Ak.

Назовем пересечением (или произведением) множеств

А и В множество C = А ∩ В, состоящее из всех элемен-

тов, принадлежащих как А, так и B.

Например, пересечение множества всех четных чи-

сел и множества всех чисел, делящихся на три, есть

множество всех четных чисел, делящихся на три.

Пересечением любого конечного числа множества Ak

называется совокупность A_kkn=1 ∩ элементов, принадлежащих каждому из множеств Ak.

Разность множеств А и В — это совокупность C =

= А\B тех элементов из А, которые не содержатся в В.

Т е о р е м а. Операции сложения и пересечения

коммутативны и ассоциативны:

A ∪ B = B ∪ A, А ∩ В = B ∩ A,

(A ∪ B) ∪ C = A ∪ (B ∪ C), (A ∩ B) ∩ C = A ∩ (B ∩ C).

Также выполняется закон дистрибутивности:

А ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).

Доказательство. Допустим, что x ∈ А ∩ (B ∪ C).

Тогда x ∈ А и x ∈ B ∪ C, т.е. x ∈ B или x ∈ C (или и то

и другое). Значит, x ∈ A ∩ B или x ∈ A ∩ C, так что

x ∈ (A ∩ B) ∪ (A ∩ C). Таким образом, А ∩ (B ∪ C) =

= (A ∩ B) ∪ (A ∩ C).

Предположим теперь, что x ∈ (A ∩ B) ∪ (A ∩ C).

Тогда x ∈ A ∩ B или x ∈ A ∩ C. Таким образом, x ∈ A и

x ∈ B ∪ C. Значит, x ∈ A ∩ (B ∪ C), так что (A ∩ B) ∪

∪ (A ∩ C) = A ∩ (B ∪ C ).

Следовательно, А ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C). Ут-

верждение доказано.

6. Ограниченные последовательности (sup x, Inf x).

Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества {x}  (обозначение  sup{x}).

Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества  {x} (обозначение inf{x}).

         Более точно, эти понятия выражаются следующими свойствами:

Супремум  sup{x} 1.  . 2.  .

Инфимум  inf{x} 1.  . 2.  .

         Заметим, что sup{x} и inf{x} могут как принадлежать, так и не принадлежать числовому множеству {x}  .

         Теорема о существовании супремума и инфимума числового множества.

         Если числовое множество {x} не пусто и ограничено сверху, то у него существует sup{x}.

         Если числовое множество {x} не пусто и ограничено снизу, то у него существует inf{x}.