Метод наискорейшего спуска

Основным недостатком градиентного метода является необходимость частого вычисления производннх от R(х). Этого недостатка лишен метод наискорейшего спуска, который заключается в следующем.

В текущей точке вычисляется grad R(х), и затем в направлении градиента ищется тinR(х). Практически зто может быть осуществлено любым методом одномерной оптимизации (поиск по одному направленню — направленню градиента), наиболее часто используется сканирование до первого локального минимума по направлению grad R(х).

В результате вдали от оптимума эффективность метода повышается, мы быстреє попадаем в район оптимума, в окрестности которого зффективность метода снижается из-за частой смены направлення поиска й приближается к зффективности метода гра­диента.

Метод, как и все градиентные метод, обладает невьісокой зффективностью в овражньїх функциях. В ряде случаев можно повисить скорость вихода в район оптимума предьявлением невисоких требований к точности поиска шіп по направлению (задается величиной h — шагом поиска по направлению).

Условием окончания может являться малость модуля градиента R(х) |gгаd R(x)|< . Можно также использовать и малость приращений по переменннм в результате шага, но только в том случае, если на данном шаге мы "проскочили" оптимум, иначе может сказаться, что малость шага обусловлена не близостью к оптиму­му, а малостью коэффициента пропорциональности шага h.

В ряде случаев используют уменьшение шага поиска оптиму­ма по направлению после каждой смены направлення. Это позво-ляет с большей точностью каждьій раз находить оптимум, но рез-ко снижает зффективность поиска в овражньїх функциях. Метод используется для локализации "дна оврага" в специальньїх ов­ражньїх методах. Условием окончания поиска в зтом случае явля­ется достижение заданной малой величини шага.

Одна из возможнмх траекторий поиска минимума двумерной функции методом наискорейшего спуска приведена на рис. 17.

Метод тяжелого шарика

Метод базируется на аналогии с движением "тяжелого" материального шарика по наклонной поверхности. Скорость шарика при движении вниз будет возрастать, и он будет стремиться занять нижнее положение, т.е. точку минимума. При выводе дифференциального уравнения движения шарика учитывается его масса и вязкость среды, которые влияют на характер его движения, т.е. поиска min R(x).

В дискретном варианте траектория поиска описывается сле­дующим алгоритмом:

При  = 0 метод превращается в обыкновенный градиентный. При  = 1 поиск не затухает, следовательно, при 0 <  < 1 можно получать различную эффективность метода, которая будет зависеть и от h. Вдали от оптимума поиск будет ускоряться, а вблизи возможны колебания около точки min R(x).

К недостаткам метода относится необходимость задания сразу двух неформальных параметров, определяющих эффективность поиска. К достоинствам метода, помимо ускорения движения вдали от оптимума, относится возможность "проскока" мелких локальных "ямок" (минимумов) за счет "инерционности шарика", т.е. можно решать и задачу глобальной оптимизации для функции R(x) с одним явно выраженным минимумом и многими "мелкими".

Одна из возможных траекторий поиска минимума двумерной функции методом тяжелого шарика приведена на рис. 17.

МНОГОМЕРНАЯ БЕЗГРАДИЕНТНАЯ ОПТИМИЗАЦИЯ

В данном разделе рассматриваются численные методы опти­мизации, у которых величина и направление шага к оптимуму формируются однозначно по определенным детерминированным функциям в зависимости от свойств критерия оптимальности в окрестности текущей точки без использования производных (т.е. градиента). Все алгоритмы имеют итерационный характер и вы­ражаются формулой

Основная особенность рассматриваемой группы методов — отсутствие вычисления градиента критерия оптимальности. Ряд методов прямого поиска ба­зируется на последователь­ном применении одномер­ного поиска по переменным или по другим задаваемым направлениям, что облегча­ет их алгоритмизацию применение. Как и для градиентных методов, на рис.18 приводятся лишь по одной из возможных траекторий поиска каждым из ниже рассматриваемых методов. Кроме того, также для всех приведенных траекторий выбраны различные начальные условия, с тем чтобы не загромождать построения.

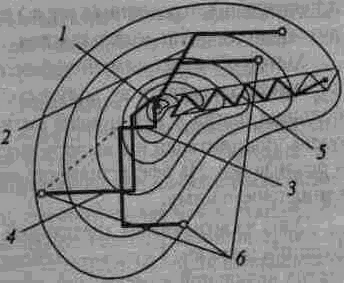
Рис. 18. Иллюстрация траекторий поиска минимума функции безградиентными детерминированными методами: 1 — оптимум; 2 — траектория метода параллельных ка­сательных; 3 — траектория метода Гаусса — Зайделя; 4 — траектория метода Розенброка; 5 — траектория симплексного метода; 6 — начальные точки поиска