Проверочный расчет на изгибную прочность
Рассмотрим цилиндрическую передачу с прямым зубом. Максимальные напряжения возникают в заделке (у основания зуба), когда сила находится у окружности вершин и передается одной парой зубьев. Самой опасной является точка А1 (Рис. 3.16), т.к. усталостные трещины и разрушения начинаются с растянутой стороны зубьев. В опасной точке А1 максимальные напряжения от изгиба и сжатия равны:
Где
-
теоретический коэффициент концентрации
напряжений у основания зуба.
После
замены 
на 
и введения для косозубых передач
коэффициентов 
и 
формула примет вид:
где
- удельная окружная сила,
- коэффициент, учитывающий перекрытие
зубьев,
- коэффициент, учитывающий наклон зуба
(получен экспериментально), 
- коэффициент формы зуба.
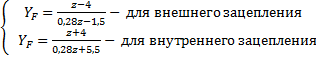(3.25)
При расчете косозубых передач по формуле (3.24) = = 1.
- коэффициент торцевого перекрытия.
должен быть для прямозубых передач 
Предельные напряжения изгиба при одностороннем приложении нагрузки (цикл с коэффициентом ассиметрии R =0) для стальных зубчатых колёс
где
-
максимальные предельные напряжения
изгиба, не вызывающие остаточных
деформаций или хрупкого разрушения
Для зубчатых колес из стали:
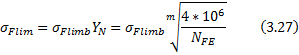
– предел выносливости изгибных напряжений
зуба при базовом числе циклов напряжений
и R
= 0.
Значения
пределов выносливости, зависящие от
способа термической, химико – термической
обработки зубьев и средней твердости
поверхностей приводятся в учебниках;
– коэффициент долговечности, m
= 9 для колес цементированных и азотированных
с нешлифованной поверхностью у основания
зуба; в других случаях m
= 6; 
– число циклов нагружения при изгибе.
При заданном
число циклов 
, 
( Рис а) или 
(Рис б).
При
заданном ресурсе 
число циклов 
.
Допускаемое напряжение в опасном сечении A1B1 определяется по формуле:
– Коэффициент, учитывающий влияние шероховатости поверхности
у
корня зуба (
=
1 при нешлифованных зубьях,
= 1,05…1,1 при шлифованных зубьях); 
= 1 при одностороннем вращении.
При
реверсе 
Условие прочности на изгиб:
Конические зубчатые передачи
Используются
для передачи вращения между валами с
пересекающимися осями. Их назначение
– изменить межосевой угол расположения
валов, что может сочетаться с изменением
угловых скоростей и моментов. Межосевой
угол 
обычно 90о
(Рис. 3.17),
реже используются передачи с другими
углами 
из-за сложного сложности изготовления
корпусных деталей.
Учитывая
сложность изготовления, сборки и высокую
стоимость, конические передачи
нецелесообразно использовать для
изменения частоты вращения (обычно не
более 
),
а лишь для изменения положения валов.
Передаточное отношение для конической ортогональной передачи (Рис.3.17):
и 
внешний диаметр делительной окружности
шестерни и колеса, 
и 
- углы делительного конуса шестерни и
колеса.
Наиболее распространены конические передачи с прямым (Рис.3.18а) и круговым (Рис.3.18б) зубом, последние используются обычно при V > 3 м/с.
В конических передачах вместо начальных и делительных цилиндров их функции выполняют начальные и делительные конусы.
Геометрию
конической передачи (Рис.3.17.
Рис.3.19)
характеризуют параметры:
– межосевой угол, 
– внешнее конусное расстояние, 
- угол делительного конуса, 
- угол конуса вершин, 
– угол конуса впадин. Для ортогональной
геометрической передачи с 
и
коэффициентом смещения Х = 0 используемое
в расчетах прочности среднее конусное
расстояние 
, 
, высота ножки, головки и полная высота
зуба во внешнем торцевом сечении 
, 
, 
, где 
– стандартное значение внешнего
окружного модуля.
Угол
ножки (головки) зуба: 
Угол
конуса вершин 
Угол
конуса впадин 
(3.31)
Внешний
и средний диаметр делительной окружности
– относительная ширина зубчатого венца.
Для
круговых зубьев стандартным является
нормальный модуль в среднем сечении
на середине ширины зуба.
Из треугольника О1РО2 (Рис.3.19) для прямозубых конических передач параметры эквивалентных прямозубых цилиндрических передач
(3.32):
– диаметр делительной окружности и
число зубьев эквивалентного колеса.
На конические колеса прямозубой конической передачи действуют силы
Ft=2T1/dm1;
(рис.3.20 А
– А)
Составляющие
силы
равны:
осевая
-
;
радиальная
-
.
Из
рис.3.20 видно, что при
.