2. Геометрический анализ

Целью геометрического анализа рычажного механизма является составление уравнений геометрического анализа, решение их, выделение побочных и основных решений, определяющих положения звеньев, а также исследование функций положения выходных звеньев структурных групп.

Размыкая кинематическую цепь в шарнирах А и D, приведем замкнутую цепь к открытой цепи (ветви: ОА, АBC, ЕD).

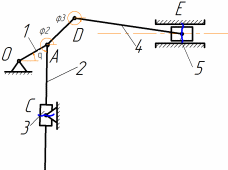
Рис. 1.5 Разомкнутые связи на схеме механизма

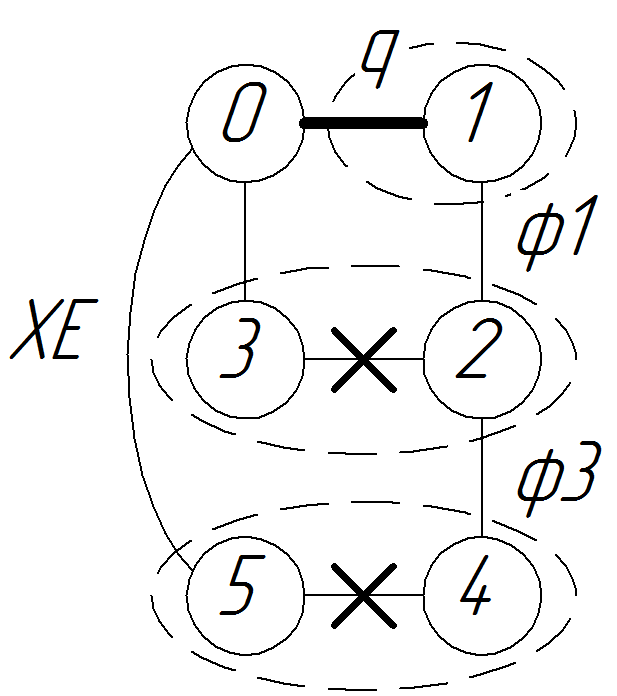
Рис. 1.6 Разомкнутые связи на структурном графе механизма

На структурной схеме и графе механизма обозначим входную координату q и 2 групповые координаты: φ₁, φ₃. Их число совпадает с числом разомкнутых связей: X_С, Y_C, X_E (в данном случае φ₁ совпадает с φ₂, поэтому получается, что групповых координат на самом деле три, но одна из них не учитывается).

1. Уравнения геометрического анализа.

Здесь и далее все неизвестные, которые необходимо определить из данной системы или из данного уравнения подчёркнуты.

Функции положения для группы I (кривошип OA):

Групповые уравнение для группы II (ВПВ):

Функции положения точки D:

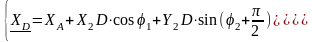
Групповые уравнения для группы III (ВВП):

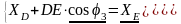
1. Решение уравнений геометрического анализа в общем виде

а) Группа ВПВ:

Перенесём все неизвестные части влево, а известные – вправо:

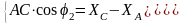
Возведём обе части в квадрат:

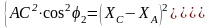
Сложим два уравнения:

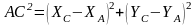
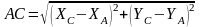
Отсюда легко можно найт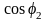и и :

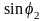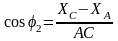
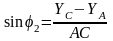
И следовательно, мы можем найти и сам угол .

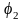б) Группа ВВП:

Напомним, что:

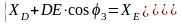
Отсюда мы можем определить :

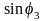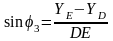
Тогда:

Здесь 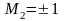, то есть существуют два решения уравнения. Этим решениям соответствуют два варианта сборки звеньев группы ВВП. На рис.2.4 один из них, соответствующий основному решению (+), показан сплошными линиями, а другой, соответствующий побочному решению (-), изображен пунктирными линиями.

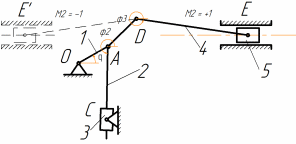
Рис.1.7 Две сборки механизма

Положение группы типа ВВП, при котором обход шарниров в последовательности A, D, E происходит по часовой стрелки, соответствует способу сборки 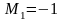, если же обход идёт против часовой стрелки, как в случае с ADE′, то способ сборки .

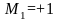В исходной схеме .

Далее найдём :

Все расчёты представлены в приложении в протоколе MathCad.

Из неравенства 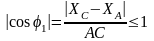можно получить условие существования группы ВПВ: , где

Из неравенства 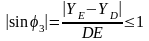получаем условие существования группы ВВП:

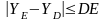
2. План 12 положений механизма

Рис.1.8. План 12 положений механизма

3. Кинематический анализ механизма

   1. Определение аналогов скоростей

Продифференцируем выражения из пункта 1.2.1. по q.

Группа I (кривошип OA)

Группа ВПВ

Находим аналоги скоростей точек B и D а также аналог угловой скорости φ2`.

Н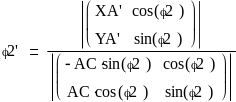 айдём аналог угловой скорости :

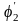С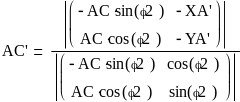 разу же определим :

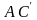Находим аналоги скорости точки D:

Группа ВВП

Находим аналог скорости точки E и аналог угловой скорости φ3`.

Дифференцируя выражение по q, мы можем найти аналог угловой скорости :

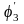Находим аналог скорости точки E: