Модуль 2. Розв’язання тригонометричних рівнянь. Заняття 6. Тригонометричні рівняння.

Рівняння називається тригонометричним, якщо невідомі в рівнянні містяться лише під знаком тригонометричних функцій, аргументи тригонометричних функцій є лінійними функціями невідомих і над тригонометричними функціями виконується лише алгебраїчні операції.

Розв’язати тригонометричне рівняння – означає знайти всі значення невідомого, при яких рівняння перетворюється на тотожність.

Тригонометричні рівняння можуть не мати розв’язків . Наприклад, не мають розв’язку рівняння та інші. Якщо тригонометричне рівняння має розв’язки, то їх безліч. Множину розв’язків тригонометричного рівняння називають загальним розв’язком. Так загальним розв’язком рівняння буде , де . Розв’язки при певних значеннях називаються частковими. Наприклад при отримаємо частковий розв’язок , а при , .

Найпростіші тригонометричні рівняння.

Найпростішими тригонометричними рівняннями є рівняння виду , де  будь-яке число.

Рівняння , має розв’язки тільки при . Розв’язки даного рівняння знаходяться по узагальнюючій формулі і .

Часткові випадки.

Якщо то .

Якщо то .

Якщо то .

Рівняння має розв’язки тільки при . Розв’язки даного рівняння знаходяться по узагальнюючій формулі і .

Часткові випадки.

Якщо то .

Якщо то .

Якщо то .

Розв’язок рівняння знаходиться по формулі .

Аналогічно, розв’язок рівняння знаходиться по формулі .

При розв’язанні найпростіших рівнянь слід пам’ятати наступні тотожності:

Приклад 6.1. Розв’яжіть рівняння .

Розв’язання.

Приклад 6.2. Розв’яжіть рівняння .

Розв’язання.

Приклад 6.3. Розв’яжіть рівняння .

Розв’язання. Дане тригонометричне рівняння розв’язків немає, бо абсолютна величина косинуса не може бути більша за одиницю.

Основні типи тригонометричних рівнянь.

Множину тригонометричних рівнянь умовно можна поділити на кілька типів. Даний поділ відносний тому, що єдиної теорії розв’язування тригонометричних рівнянь не існує. Наведемо класифікацію рівнянь подану в посібнику Г.М. Скобелєва, Елементарна математика (тригонометрія).

До першого типу тригонометричних рівнянь, належать рівняння які зводяться до найпростіших за допомогою алгебраїчних перетворень.

Приклад 6.4. Розв’яжіть рівняння

Розв’язання.

Завдання для самостійної роботи.

Розв’яжіть рівняння:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. .

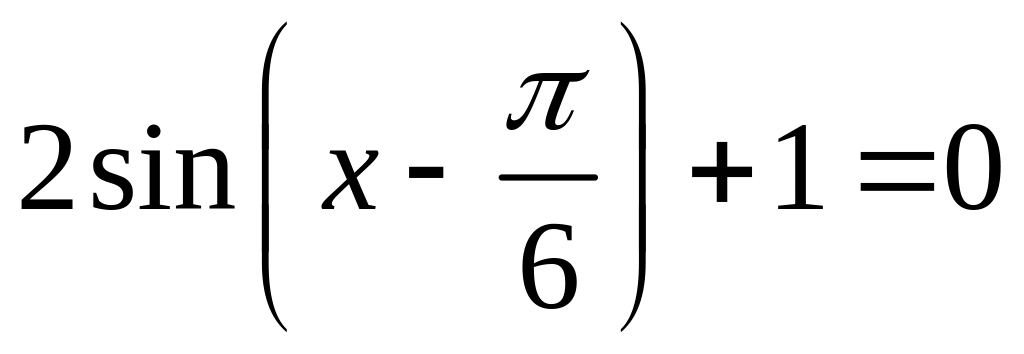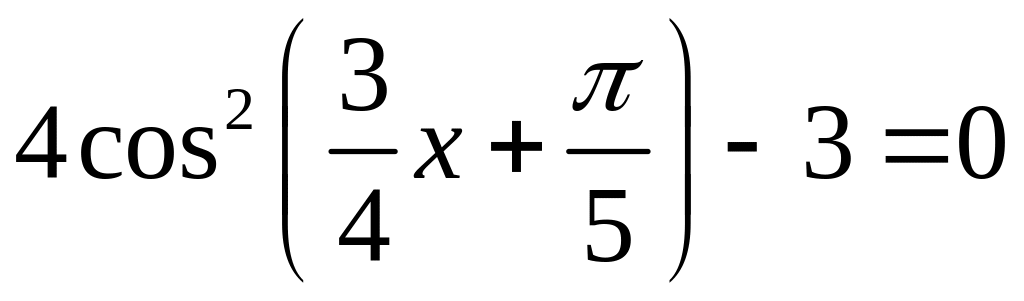Заняття 7. Тригонометричні рівняння II-IV типів.

До другого типу тригонометричних рівнянь належать рівняння, лівою і правою частинами яких є одна й та сама функція, але від різних аргументів. Наприклад, .

Для розв’язання рівнянь такого типу доцільно застосувати такі правила:

1. для виконання рівності необхідно і достатньо, щоб , або ;

2. для виконання рівності необхідно і достатньо, щоб , або ;

3. для виконання рівності і необхідно і достатньо, щоб .

Приклад 7.1. Розв’яжіть рівняння .

Розв’язання.

Приклад 7.2. Розв’яжіть рівняння .

Розв’язання.

Приклад 7.3. Розв’яжіть рівняння .

Розв’язання.

Але серія розв’язків є серед розв’язків , тому розв’язок даного рівняння визначається однією формулою

Приклад 7.4. Розв’яжіть рівняння .

Розв’язання. Поділимо ліву та праву частини рівняння на 2.

Вказаний тип рівнянь можна розв’язувати використовуючи формули перетворення суми або різниці тригонометричних формул в добуток. Для цього переносять праву частину рівняння в ліву, застосовують формулу і прирівнюють кожний співмножник до нуля, знаходячи усі розв’язки рівняння.

Приклад 7.5. Розв’яжіть рівняння .

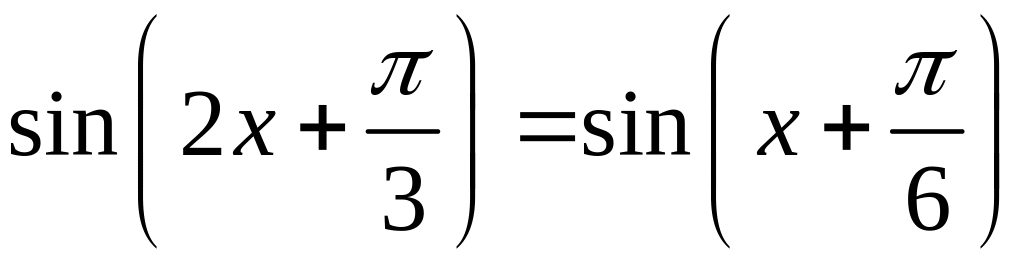Розв’язання.

,

,

До третього типу тригонометричних рівнянь належать рівняння, в одній частині яких є деяка функція, а в іншій її кофункція. Наприклад, . Для розв’язання цих рівнянь потрібно застосувати формули зведення, перейти до однієї функції і розв’язати як рівняння другого типу.

Приклад 7.6. Розв’яжіть рівняння .

Розв’язання.

,

Приклад 7.7. Розв’яжіть рівняння .

Розв’язання.

Розділимо обидві частини рівняння на . Це можливо, так як в даній умові не може дорівнювати нулю.

До четвертого типу тригонометричних рівнянь належать рівняння, в яких виконуються алгебраїчні дії над будь-якою однією функцією одного аргументу. Такі рівняння зводяться до алгебраїчних за допомогою заміни.

Приклад 7.8. Розв’яжіть рівняння .

Розв’язання.

Нехай тоді отримаємо рівняння , звідки

Приклад 7.9. Розв’яжіть рівняння .

Розв’язання.

позначимо отримаємо:

Отже вихідне рівняння рівносильне рівнянню . Розв’язком якого є множина

Приклад 7.10. Розв’яжіть рівняння .

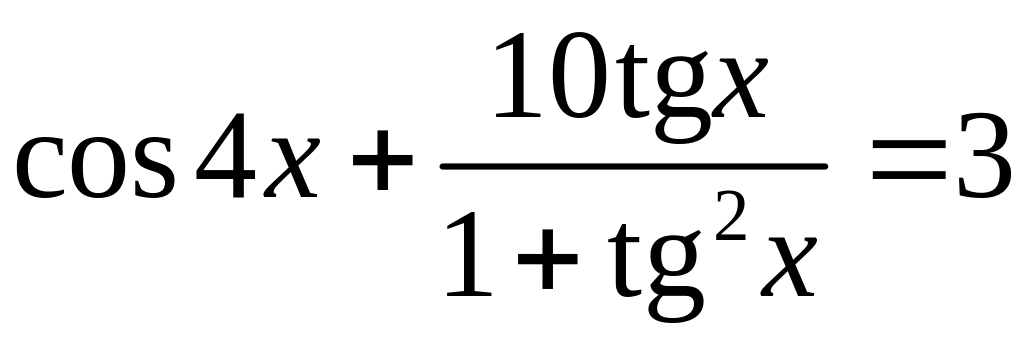Розв’язання. Використавши формулу рівняння прийме вигляд ,

.

Позначимо , тоді ,

Отже вихідне рівняння рівносильне рівнянню , звідки:

Завдання для самостійної роботи.

Розв’яжіть рівняння:

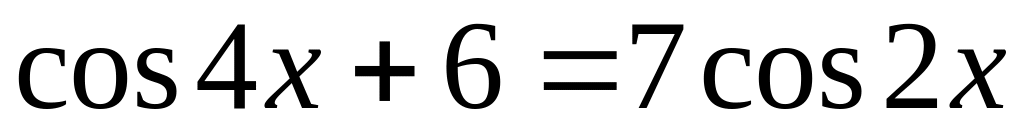1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. .