
- •Передмова
- •Модуль 1. Перетворення тригонометричних виразів. Заняття 1. Загальні відомості з тригонометрії.
- •Основні тригонометричні формули та співвідношення.
- •Заняття 2. Тотожні перетворення тригонометричних виразів.
- •Заняття 4. Перетворення тригонометричних виразів в добуток. Доведення умовних тотожностей.
- •Заняття 5. Тотожні перетворення виразів, що містять обернені тригонометричні функції.
- •Модуль 2. Розв’язання тригонометричних рівнянь. Заняття 6. Тригонометричні рівняння.
- •Найпростіші тригонометричні рівняння.
- •Основні типи тригонометричних рівнянь.
- •Заняття 7. Тригонометричні рівняння II-IV типів.
- •Заняття 8. Тригонометричні рівняння V-VI типів.
- •Заняття 9. Рівняння виду .
- •1. Спосіб введення допоміжного кута.
- •3. Спосіб зведення до однорідного рівняння.
- •Заняття 10. Тригонометричні рівняння VII-VIII типів.
- •Найпростіші тригонометричні нерівності.
- •Розв’язування тригонометричних нерівностей.
- •Заняття 13. Розв’язання тригонометричних нерівностей методом інтервалів.
- •Розв’язком нерівності будуть інтервали
- •Заняття 14. Розв’язання тригонометричних нерівностей .
- •Модуль 4. Системи тригонометричних рівнянь. Заняття 15. Розв’язання систем тригонометричних рівнянь.
- •Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – сума або різниця тригонометричних функцій.
- •Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – добуток тригонометричних функцій.
- •Заняття 16. Розв’язання систем тригонометричних рівнянь. Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – відношення тригонометричних функцій.
- •Системи рівнянь, які утримують лише тригонометричні функції.
- •Заняття 17. Рівняння та нерівності, які містять обернені тригонометричні функції.
- •Нерівності, які містять обернені тригонометричні функції.
- •Заняття 18. Контрольна робота №2.
- •Література
Заняття 4. Перетворення тригонометричних виразів в добуток. Доведення умовних тотожностей.
Розглянемо деякі способи перетворення тригонометричних виразів у добуток.
Приклад 4.1. Записати у вигляді добутку вираз
![]()
Розв’язання.
![]()


Приклад
4.2. Перетворити
в добуток
![]() .
.
Розв’язання.



Приклад
4.3. Перетворити
в добуток

Розв’язання.


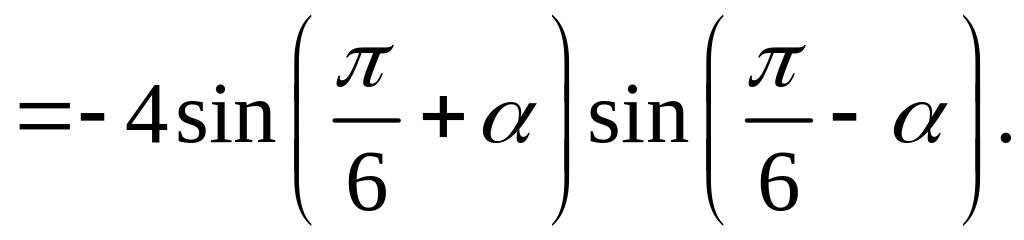
Приклад
4.4. Перетворити
в добуток
![]()
Розв’язання.
![]()


Умовними тотожностями називаються такі тотожності, які задовольняються при всіх допустимих значеннях аргументів, які в свою чергу задовольняють певні додаткові умови.
Приклад 4.5. Довести умовну тотожність
![]() ,
якщо
,
якщо
 .
.
Доведення.
Перетворимо ліву частину рівності,
враховуючи умову
 ,
тоді отримаємо:
,
тоді отримаємо:
![]()

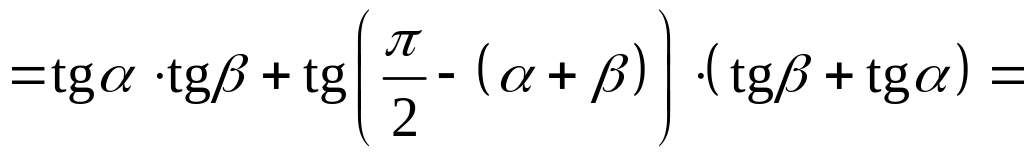
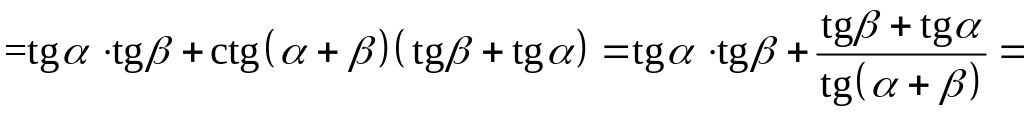

Приклад 4.6. Доведіть умовну тотожність
![]() ,
якщо
,
якщо
![]() ,
,
![]()
Доведення.
Враховуючи, що
![]() та
та
![]() отримаємо:
отримаємо:


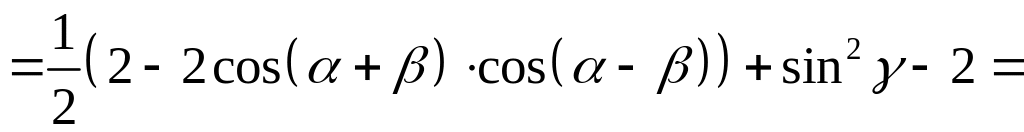
![]()
![]()
![]()
![]()
Рекомендовано провести самостійну роботу (30 хвилин).
Завдання для роботи доцільно підібрати з виконаних домашніх завдань.
Завдання для самостійної роботи.
Перетворити в добуток:
 ;
; ;
; ;
;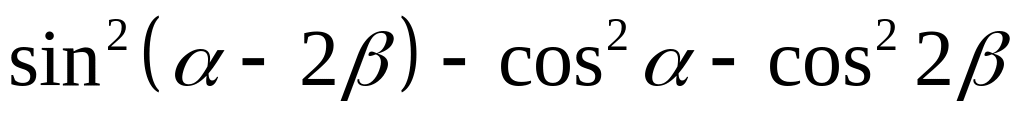 ;
; ;
; ;
; ;
;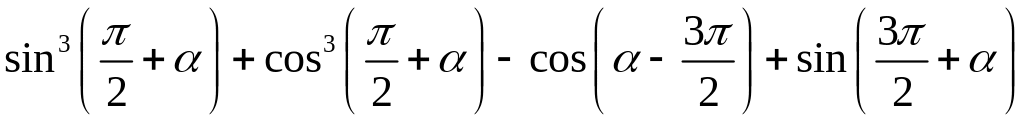 ;
;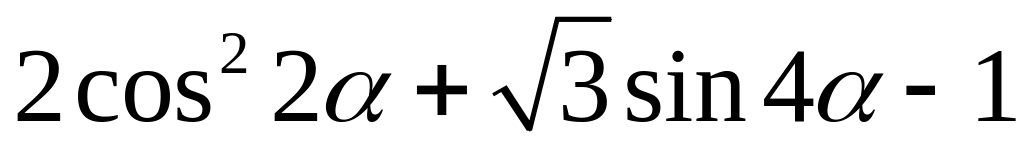 ;
; ;
; ;
; ;
;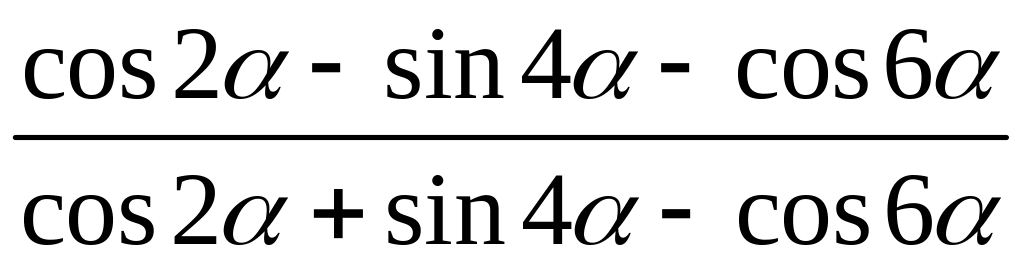 .
.
Довести умовні тотожності:
 ,
якщо
,
якщо
![]() ;
;
 ,
якщо
;
,
якщо
; ,
якщо
,
якщо ;
; ,
якщо
;
,
якщо
;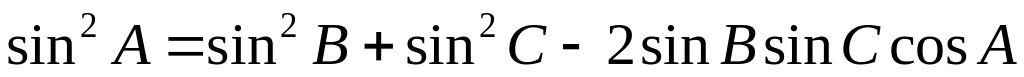 ,
якщо
;
,
якщо
;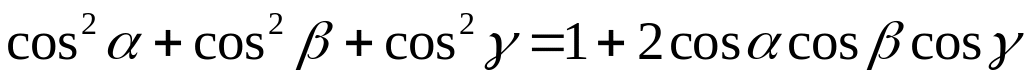 ,
якщо
,
якщо ;
; ,
якщо
;
,
якщо
; якщо
якщо
![]() ;
;
 ,
якщо
;
,
якщо
; ,
якщо
,
якщо
.
Заняття 5. Тотожні перетворення виразів, що містять обернені тригонометричні функції.
Функції
![]() ,
,
![]() ,
,
![]() ,
,
![]() називаються оберненими тригонометричними
функціями або аркфункціями.
називаються оберненими тригонометричними
функціями або аркфункціями.
Зазначимо деякі важливі тотожності:
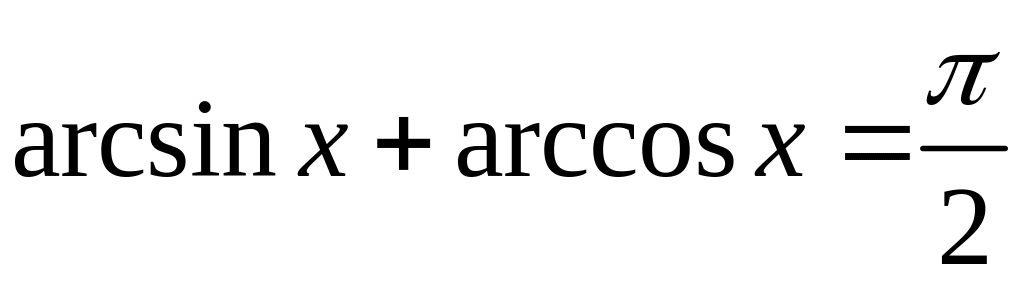 ,
,
 .
.
Розглянемо формули залежності між аркфункціями.
Нехай
,
де
![]() ,
і
,
і
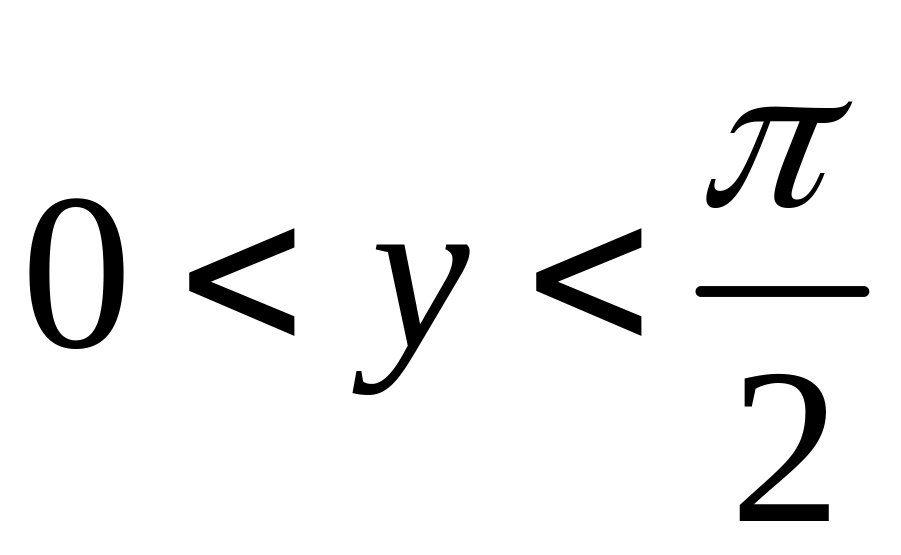 ,
тоді
,
тоді
![]() .
Знайдемо
.
Знайдемо
![]()
![]() ,
,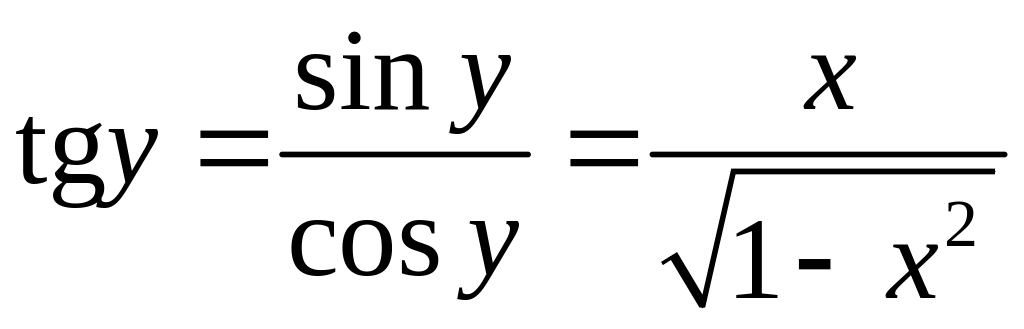 ,
, .
.
З цих співвідношень, враховуючи, що дістанемо наступні рівності:
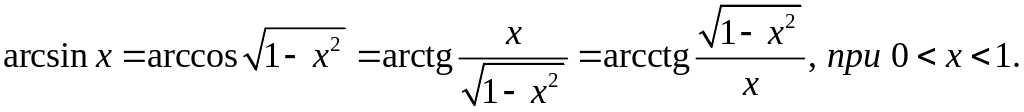
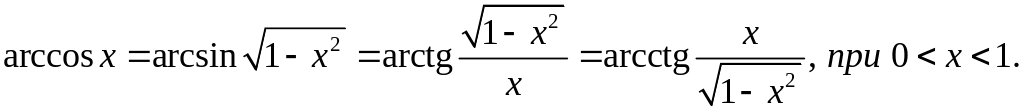
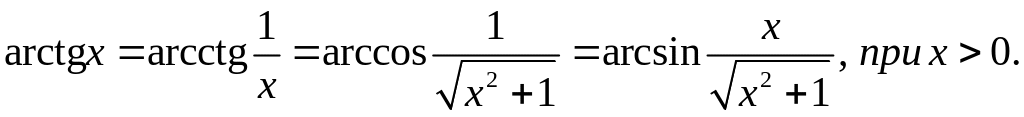
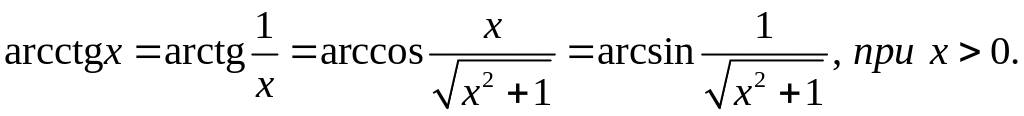
Якщо
![]() ,
то перед застосуванням формул слід
змінити знак аргументу, використавши
наступні співвідношення:
,
то перед застосуванням формул слід
змінити знак аргументу, використавши
наступні співвідношення:

Приклад
5.1. Обчисліть:
а)
 ;
б)
;
б)
 ;
в)
;
в) ;
г)
;
г)![]() .
.
Розв’язання.
а)
 ;
;
б)
 ;
;
в)
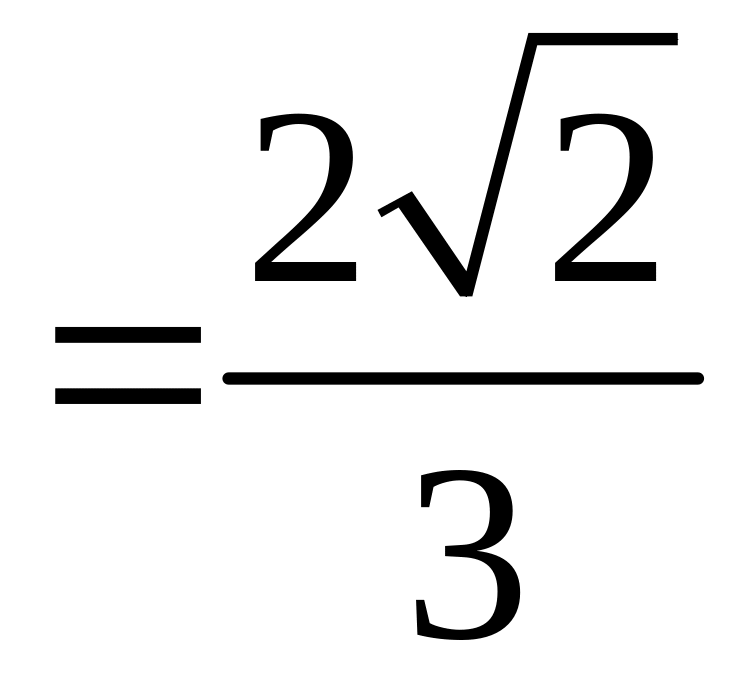 ;
;
г)

Приклад
5.2. Обчисліть
 .
.
Розв’язання.
Для обчислення даного виразу слід
скористатися формулою додавання
![]() ,
враховуючи, що
,
враховуючи, що
 ,
а
,
а
 .
Одержимо:
.
Одержимо:



Приклад
5.3. обчисліть
 .
.
Розв’язання.
В даному випадку потрібно скористатися
формулою
 ,
попередньо перетворивши
,
попередньо перетворивши
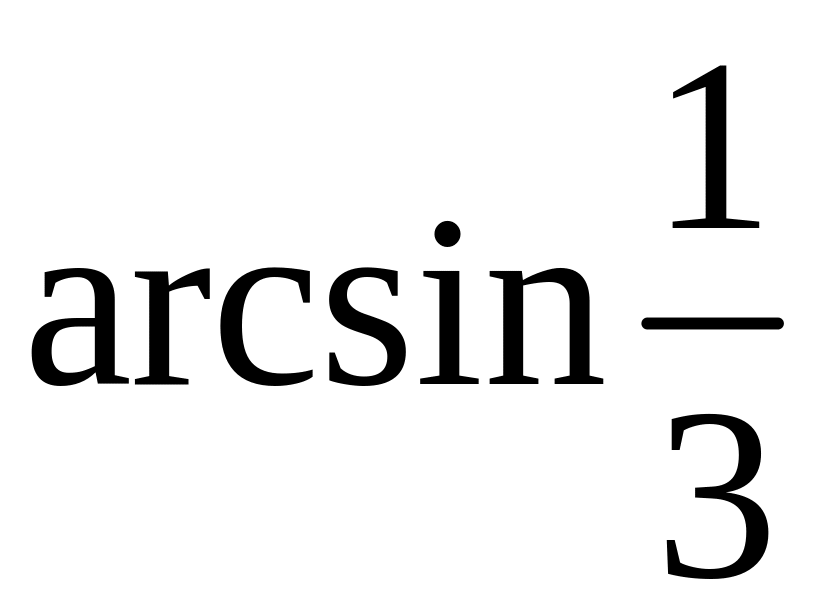 в
в
![]() з відповідним аргументом.
з відповідним аргументом.

 .
.
Приклад
5.4. Обчисліть
 .
.
Розв’язання.
Нехай
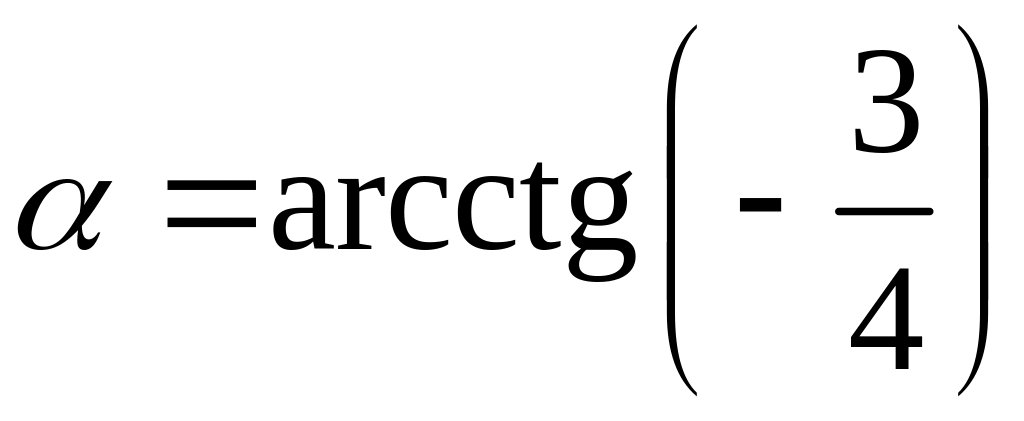 ,
тоді
,
тоді
 .
врахувавши,
що
.
врахувавши,
що
 ,
то
,
то
 .
Для знаходження
.
Для знаходження
![]() ,
використаємо формулу
,
використаємо формулу
 ,
тому спочатку потрібно знайти
,
тому спочатку потрібно знайти
![]() .
З формули
.
З формули
 ,
,
 врахувавши, що
врахувавши, що
 ,
знайдемо
,
знайдемо
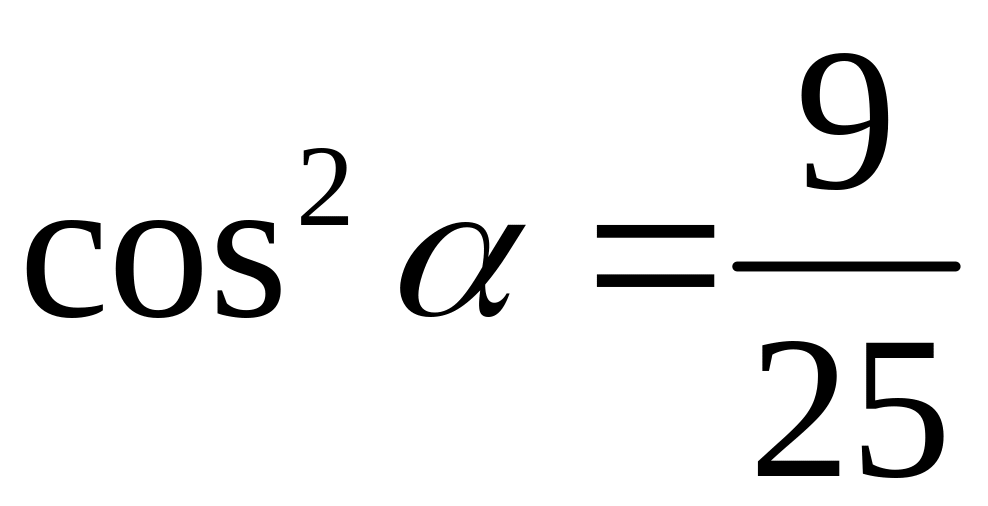 .
Так як
в інтервалі
.
Так як
в інтервалі
![]() то
то
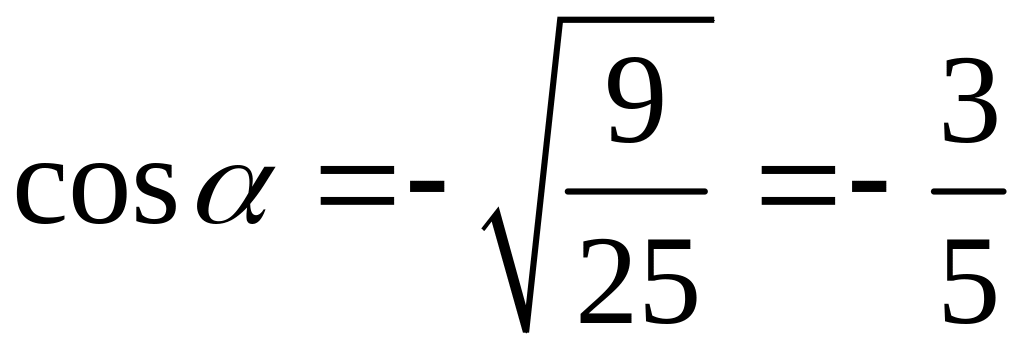 .
Отже
.
Отже
 і враховуючи, що
і враховуючи, що
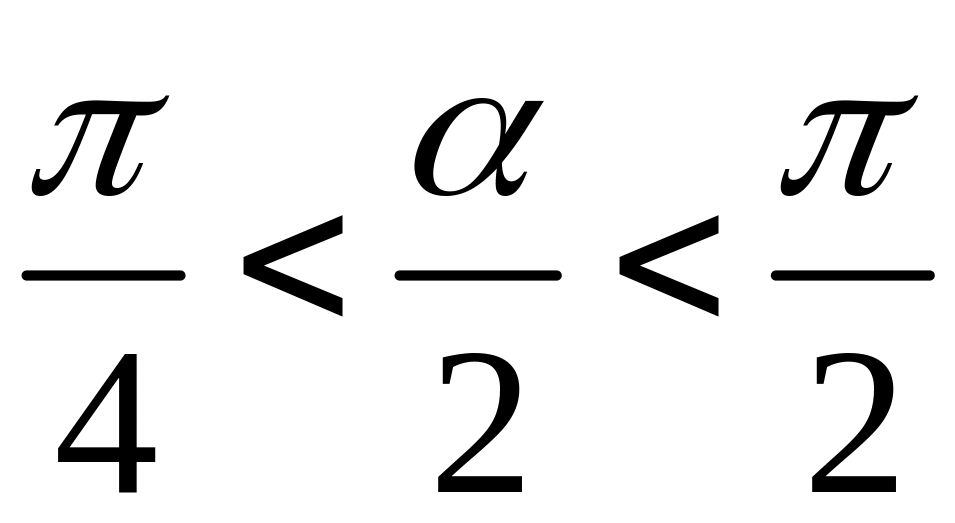 і на даному інтервалі синус приймає
лише додатних значень, то
і на даному інтервалі синус приймає
лише додатних значень, то
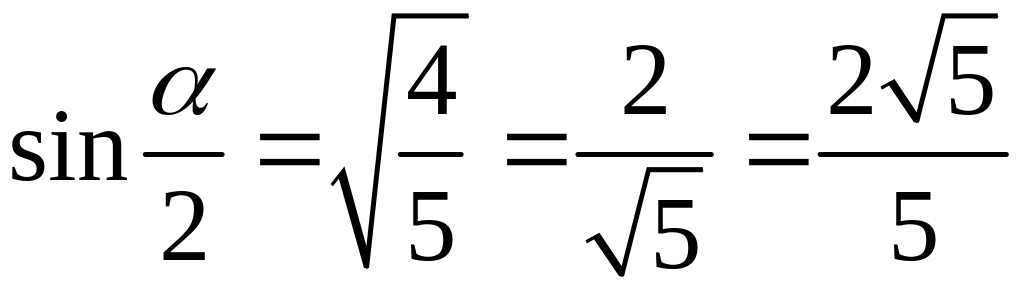 .
Таким чином
.
Таким чином
 .
.
Приклад
5.5. Обчисліть
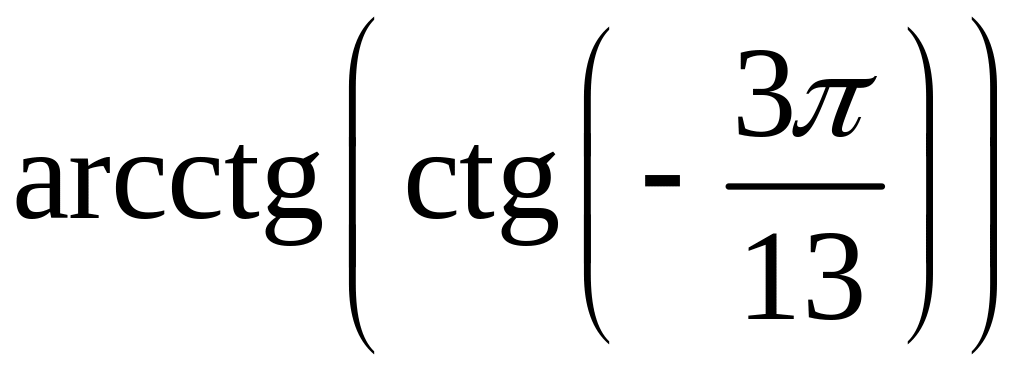 .
.
Розв’язання.
Нехай
 ,
тоді
,
тоді
![]() і
і
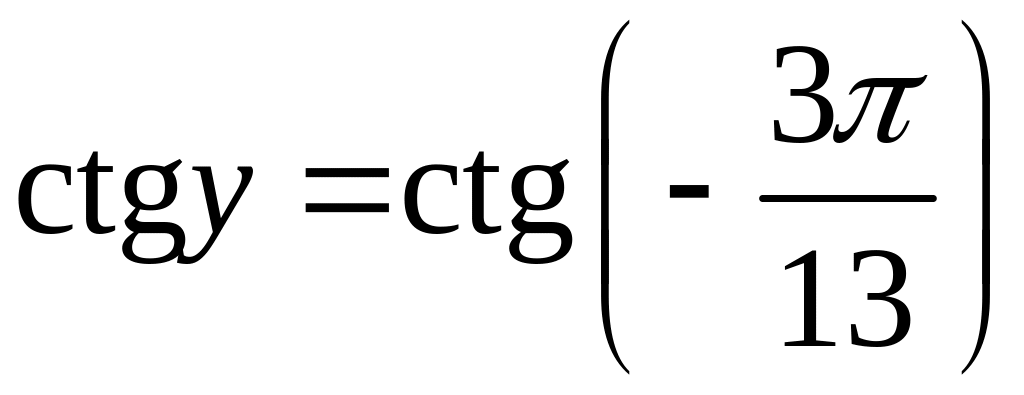 .
Але
.
Але
 ,
враховуючи, що
,
враховуючи, що
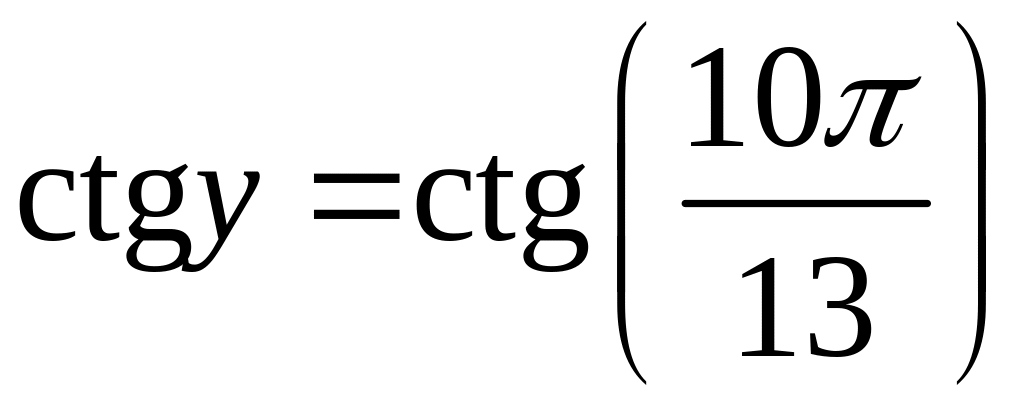 і
і
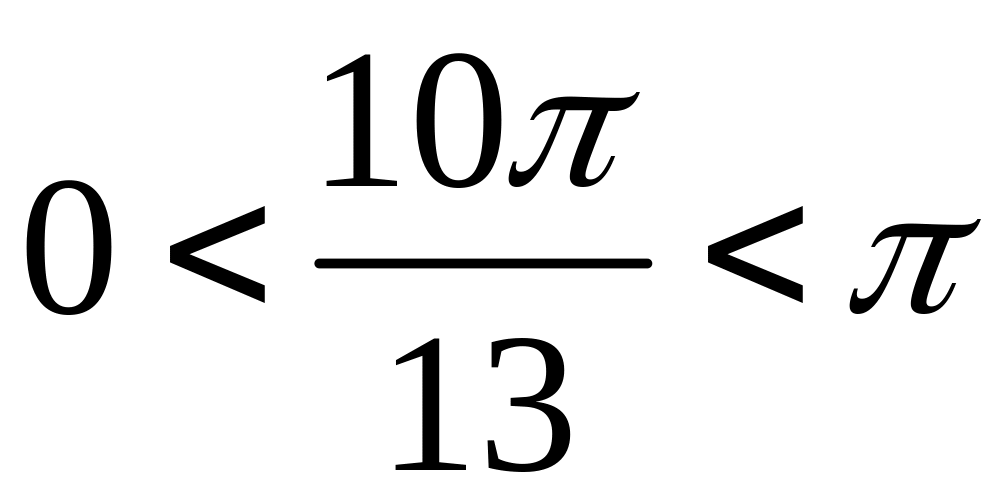 отримаємо:
отримаємо:
 .
.
Приклад
5.6. Довести
тотожність
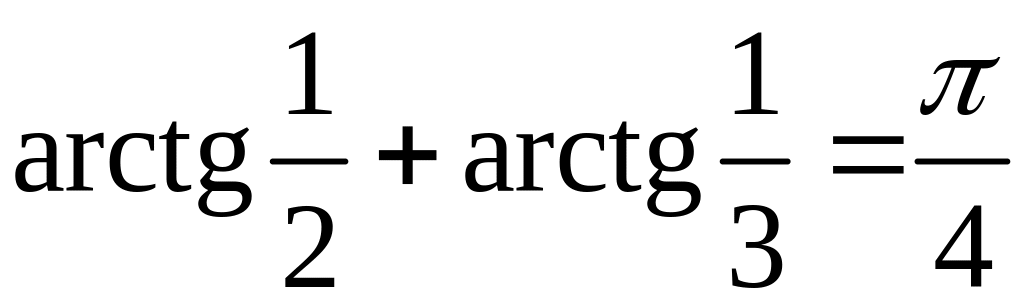 .
.
Доведення. Обчислимо значення тангенса від обох частин рівності:
 ;
;
 .
.
Але
тотожність, ще недоведена бо існує
безліч кутів, тангенс яких дорівнює 1.
Для переконання, що сума
 дорівнює
дорівнює
![]() ,
слід довести, що сума попадає в той самий
інтервал монотонності, що й
,
а саме в інтервал
,
слід довести, що сума попадає в той самий
інтервал монотонності, що й
,
а саме в інтервал
 .
.
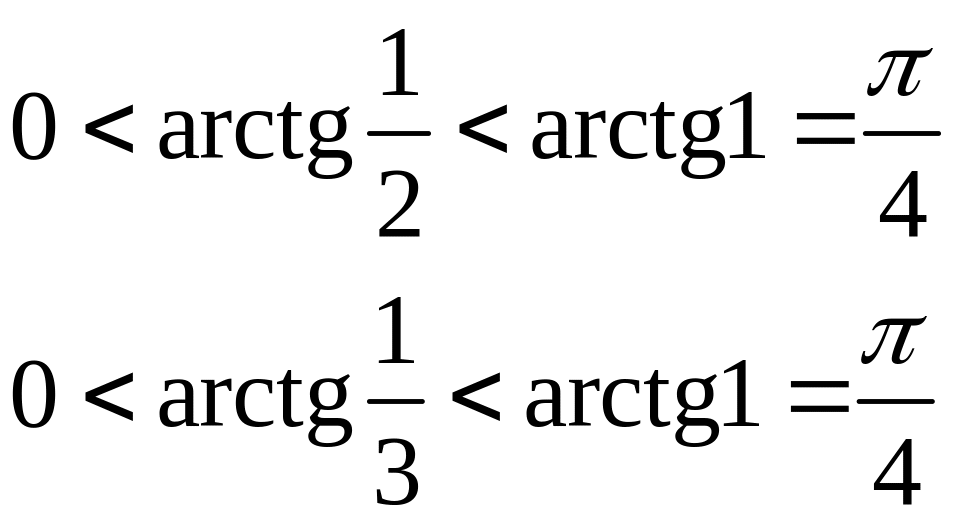
Додамо почленно обидві нерівності. Отримаємо
 .
.
Оскільки дуги кутів і належать одному інтервалу монотонності і мають однакові тангенси, то вони рівні. Отже тотожність доведено.
Завдання для самостійної роботи.
Обчисліть:
 ;
; ;
; ;
;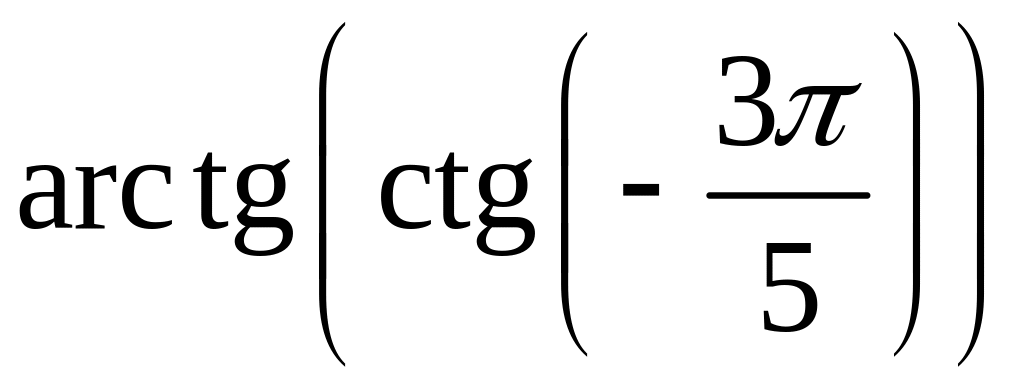 ;
; ;
;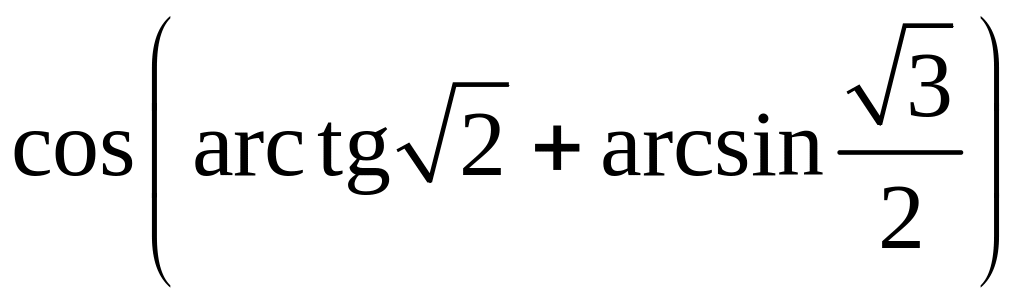 ;
; ;
; ;
; ;
; ;
; ;
; ;
;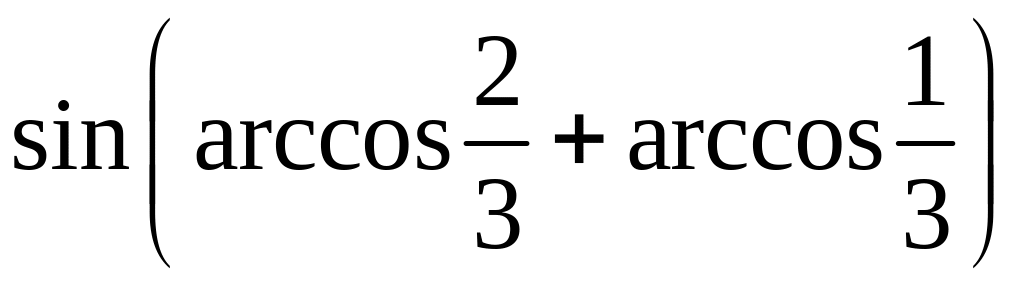 ;
; ;
;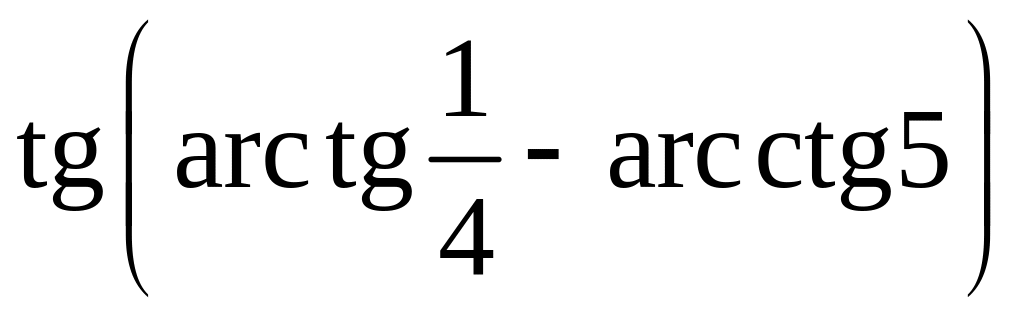 .
.
Довести тотожності:
 ;
;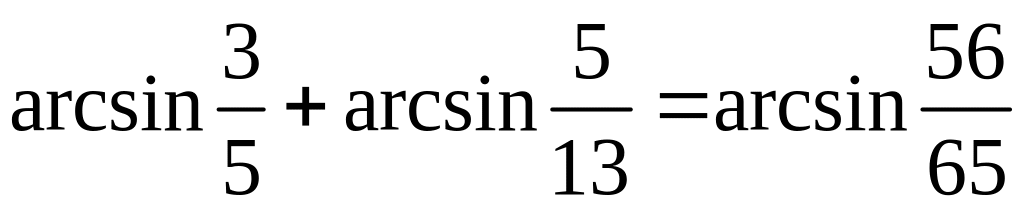 ;
; ;
; ;
;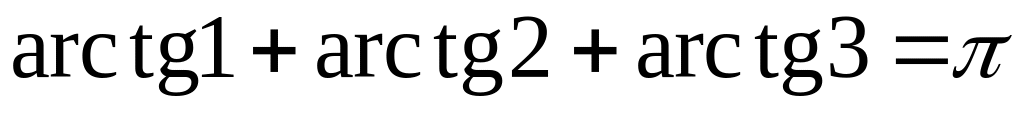 ;
; ;
; ;
; .
.
