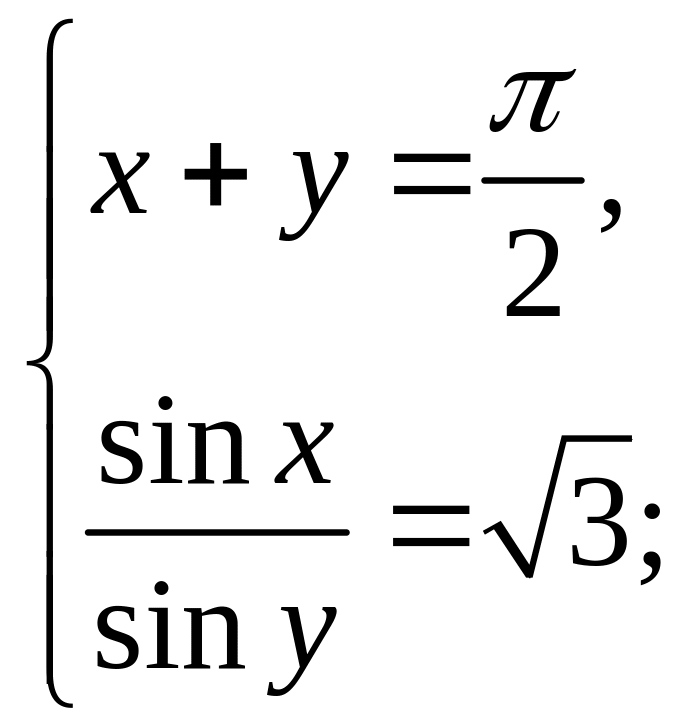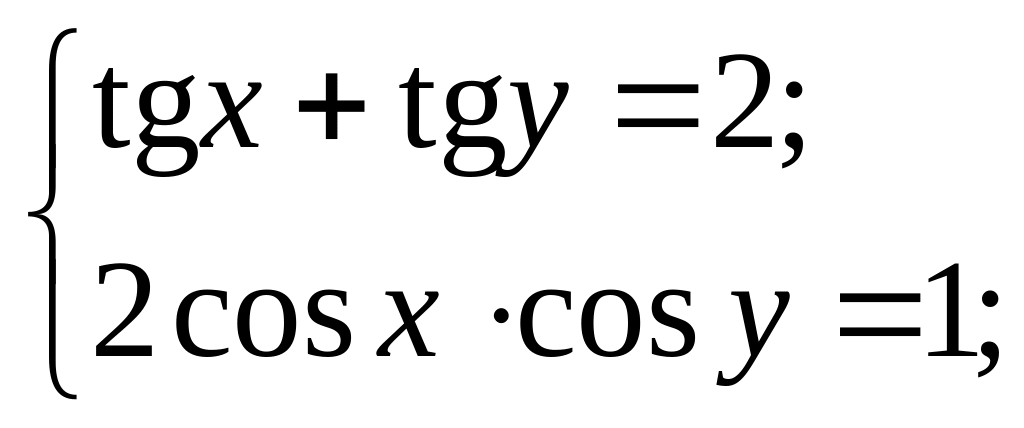- •Передмова
- •Модуль 1. Перетворення тригонометричних виразів. Заняття 1. Загальні відомості з тригонометрії.
- •Основні тригонометричні формули та співвідношення.
- •Заняття 2. Тотожні перетворення тригонометричних виразів.
- •Заняття 4. Перетворення тригонометричних виразів в добуток. Доведення умовних тотожностей.
- •Заняття 5. Тотожні перетворення виразів, що містять обернені тригонометричні функції.
- •Модуль 2. Розв’язання тригонометричних рівнянь. Заняття 6. Тригонометричні рівняння.
- •Найпростіші тригонометричні рівняння.
- •Основні типи тригонометричних рівнянь.
- •Заняття 7. Тригонометричні рівняння II-IV типів.
- •Заняття 8. Тригонометричні рівняння V-VI типів.
- •Заняття 9. Рівняння виду .
- •1. Спосіб введення допоміжного кута.
- •3. Спосіб зведення до однорідного рівняння.
- •Заняття 10. Тригонометричні рівняння VII-VIII типів.
- •Найпростіші тригонометричні нерівності.
- •Розв’язування тригонометричних нерівностей.
- •Заняття 13. Розв’язання тригонометричних нерівностей методом інтервалів.
- •Розв’язком нерівності будуть інтервали
- •Заняття 14. Розв’язання тригонометричних нерівностей .
- •Модуль 4. Системи тригонометричних рівнянь. Заняття 15. Розв’язання систем тригонометричних рівнянь.
- •Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – сума або різниця тригонометричних функцій.
- •Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – добуток тригонометричних функцій.
- •Заняття 16. Розв’язання систем тригонометричних рівнянь. Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – відношення тригонометричних функцій.
- •Системи рівнянь, які утримують лише тригонометричні функції.
- •Заняття 17. Рівняння та нерівності, які містять обернені тригонометричні функції.
- •Нерівності, які містять обернені тригонометричні функції.
- •Заняття 18. Контрольна робота №2.
- •Література
Заняття 16. Розв’язання систем тригонометричних рівнянь. Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – відношення тригонометричних функцій.
Приклад 16.1. Розв’яжіть систему рівнянь:

Розв’язання. Виразимо через і підставимо в друге рівняння.
 ,
,
 ,
,
 .
.
Знайдемо
значення
 і
і
 .
.

 .
.
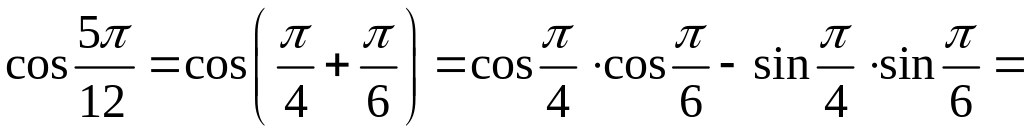
 .
.
Отримаємо: ,
,
 ,
,
 ,
,
Так
як
![]() ,то
,то
![]() ,
тоді
,
тоді
 і
і
 .
.
Загальний
розв’язок системи: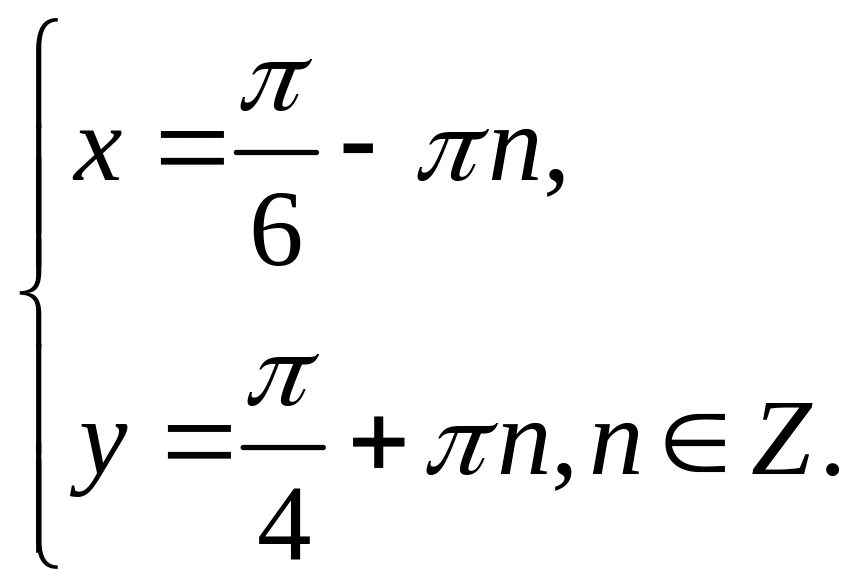
Приклад 16.2. Розв’яжіть систему рівнянь:

Розв’язання.
Виразимо
через
і підставимо в друге рівняння.
![]() ,
,
![]() ,
,
![]() ,
якщо
,
якщо
![]() ,
то отримаємо
,
то отримаємо
![]() .
.
Тоді
 і
і
 .
Загальним розв’язком системи буде:
.
Загальним розв’язком системи буде:

Приклад 16.3. Розв’яжіть систему рівнянь:

Розв’язання.
Перетворимо друге рівняння системи
 .
До даного рівняння застосуємо похідну
пропорції
.
До даного рівняння застосуємо похідну
пропорції
 ,
де
,
де
![]() ,
,
![]() ,
,
![]() ,
,![]() :
:
 ,
,
 ,
,
 ,
,
![]() ,
,


Приклад 16.4. Розв’яжіть систему рівнянь:

Розв’язання.
 ,
застосуємо до даного рівняння похідну
пропорції
,
отримаємо:
,
застосуємо до даного рівняння похідну
пропорції
,
отримаємо:
 ,
,
 ,
,
 ,
,
 ,
,
,
,
 ,
,


Системи рівнянь, які утримують лише тригонометричні функції.
Приклад 16.5. Розв’яжіть систему рівнянь:

Розв’язання. Скориставшись загальними формулами, прийдемо до системи:
 (*)
(*)
Звідки
знайдемо

Якщо
розв’язок першого рівняння системи
(*) записати у вигляді сукупності
 ;
;
 ,
а розв’язок другого рівняння у вигляді
сукупності
,
а розв’язок другого рівняння у вигляді
сукупності
 ;
; ,
то отримаємо сукупність чотирьох систем:
,
то отримаємо сукупність чотирьох систем:





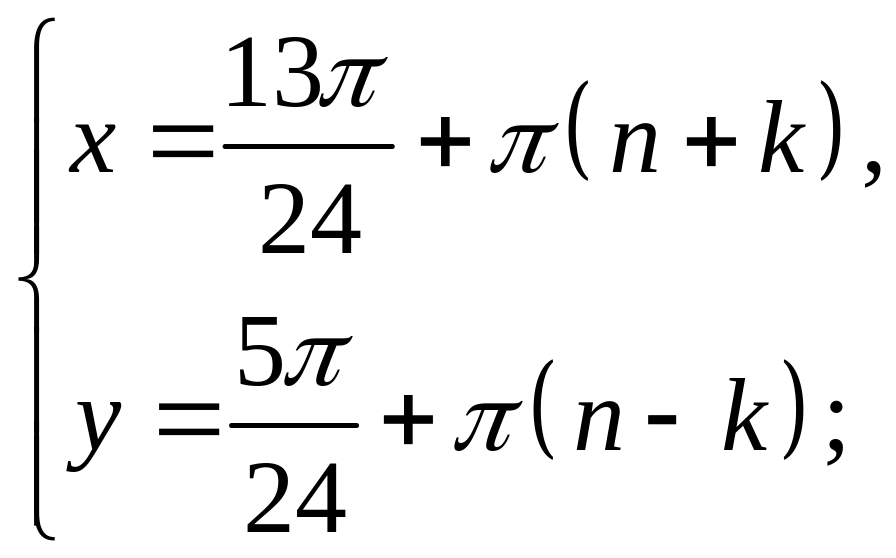


Дана сукупність є розв’язком вихідної системи. Такий запис розв’язку досить об’ємний ніж попередній, але більш наглядний, тому доречно надавати йому перевагу.
При розв’язанні першого рівняння системи використовується параметр , а другого – параметр .
Використання одного параметру приведе до втрати розв’язків системи.
Приклад 16.6. Розв’яжіть систему рівнянь:

Розв’язання.
Представимо друге рівняння системи у
вигляді
 ,
тоді
,
тоді
 і початкова система буде рівносильна
такій системі:
і початкова система буде рівносильна
такій системі:
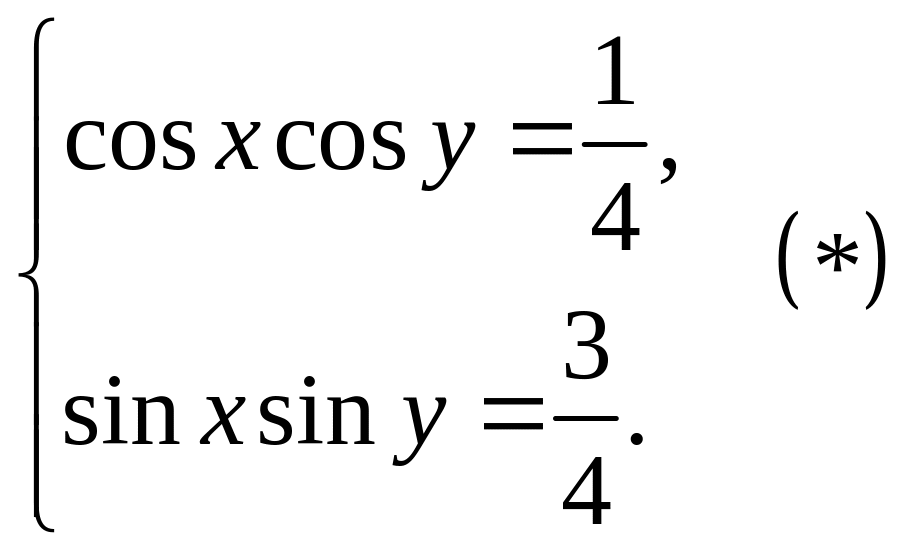
Замінимо перше рівняння системи сумою рівнянь цієї ж системи, а друге різницею першого і другого рівняння.


Розв’язуючи
систему знаходимо
 або
або
 і
і

Звідки одержимо остаточний розв’язок системи:
 і
і

Приклад 16.7. Розв’яжіть систему рівнянь:

Розв’язання.
Використавши рівність
 ,
друге рівняння системи запишемо у
вигляді
,
друге рівняння системи запишемо у
вигляді
 .
Тоді отримаємо систему рівнянь:
.
Тоді отримаємо систему рівнянь:

Розділимо перше рівняння утвореної системи на друге. Отримаємо:
 .
.
Отже
 ,
і
,
і
 ,
тоді
,
тоді
 .
.
Піднесемо
рівність
до квадрату
 і додавши з попередньою рівністю
отримаємо:
і додавши з попередньою рівністю
отримаємо:
 ,
, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Розглянемо два можливих варіанти розв’язання отриманого рівняння:
1)
![]() ,
,
![]() .
Розв’язуючи дане рівняння робимо
висновок, що дискримінант даного рівняння
менше нуля, отже дане рівняння дійсних
коренів немає.
.
Розв’язуючи дане рівняння робимо
висновок, що дискримінант даного рівняння
менше нуля, отже дане рівняння дійсних
коренів немає.
2)
![]() ,
,
![]() ,
,

Перше
рівняння даної сукупності немає
розв’язку. Розв’яжемо друге рівняння:
![]() ,
,
![]() .
Розглянемо два випадки:
.
Розглянемо два випадки:
а)
![]() ,
тоді з першого рівняння початкової
системи
,
тоді з першого рівняння початкової
системи
![]() отримаємо,
отримаємо,
![]() ,
,
![]() .
Враховуючі отримані рівняння знайдемо
загальний розв’язок системи
.
Враховуючі отримані рівняння знайдемо
загальний розв’язок системи

б)
![]() ,
аналогічно отримаємо
,
аналогічно отримаємо
![]() і знайдемо загальний розв’язок системи
і знайдемо загальний розв’язок системи

Приклад 16.8. Розв’яжіть систему рівнянь:

Розв’язання.
Якщо
,
то з першого рівняння системи отримаємо
 ,
а якщо
,
а якщо
![]() ,
то рівності рівняння не виконуються.
Підставимо рівність
в друге рівняння системи. Отримаємо:
,
то рівності рівняння не виконуються.
Підставимо рівність
в друге рівняння системи. Отримаємо:
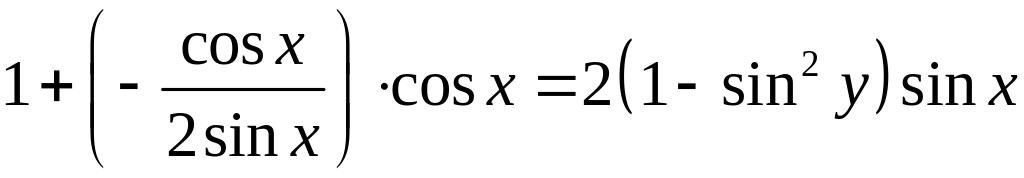 ,
,
 ,
,
 ,
,
 .
.
Запишемо
дві серії розв’язків:
 і
і
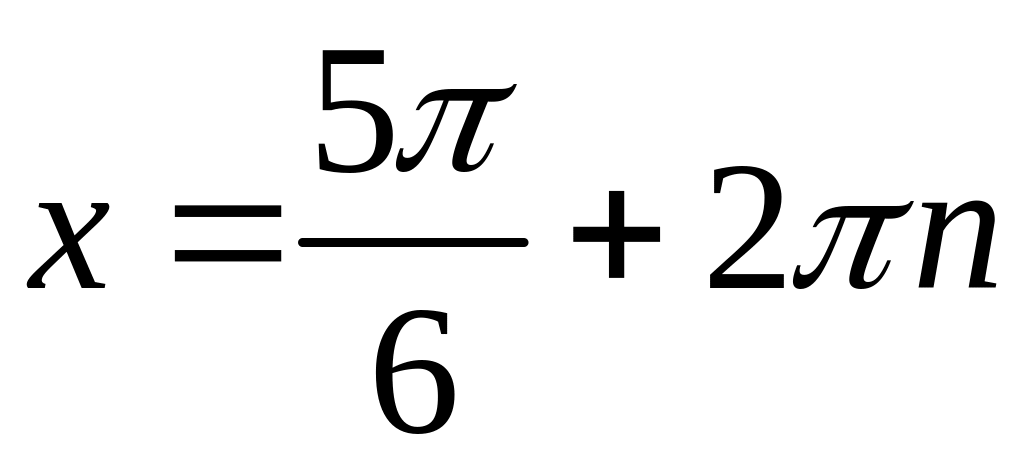 .
З рівності
,
знайдемо значення змінної
.
Розглянемо два випадки:
.
З рівності
,
знайдемо значення змінної
.
Розглянемо два випадки:
а)
 ,
,
 ,
,
 ,
,
 .
.
Тоді

б)
 ,
,
 ,
,
 ,
,
 .
.
Тоді

Завдання для самостійної роботи.
Розв’яжіть систему рівнянь.