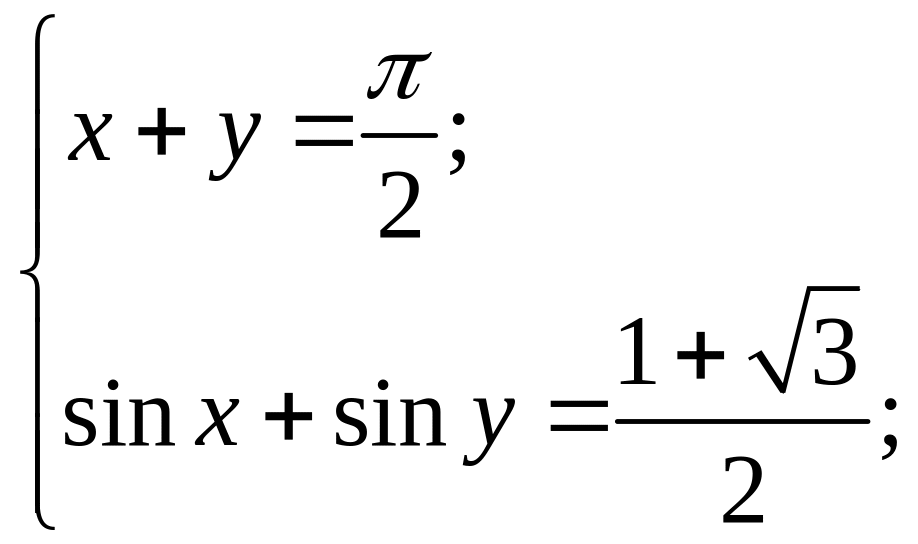- •Передмова
- •Модуль 1. Перетворення тригонометричних виразів. Заняття 1. Загальні відомості з тригонометрії.
- •Основні тригонометричні формули та співвідношення.
- •Заняття 2. Тотожні перетворення тригонометричних виразів.
- •Заняття 4. Перетворення тригонометричних виразів в добуток. Доведення умовних тотожностей.
- •Заняття 5. Тотожні перетворення виразів, що містять обернені тригонометричні функції.
- •Модуль 2. Розв’язання тригонометричних рівнянь. Заняття 6. Тригонометричні рівняння.
- •Найпростіші тригонометричні рівняння.
- •Основні типи тригонометричних рівнянь.
- •Заняття 7. Тригонометричні рівняння II-IV типів.
- •Заняття 8. Тригонометричні рівняння V-VI типів.
- •Заняття 9. Рівняння виду .
- •1. Спосіб введення допоміжного кута.
- •3. Спосіб зведення до однорідного рівняння.
- •Заняття 10. Тригонометричні рівняння VII-VIII типів.
- •Найпростіші тригонометричні нерівності.
- •Розв’язування тригонометричних нерівностей.
- •Заняття 13. Розв’язання тригонометричних нерівностей методом інтервалів.
- •Розв’язком нерівності будуть інтервали
- •Заняття 14. Розв’язання тригонометричних нерівностей .
- •Модуль 4. Системи тригонометричних рівнянь. Заняття 15. Розв’язання систем тригонометричних рівнянь.
- •Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – сума або різниця тригонометричних функцій.
- •Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – добуток тригонометричних функцій.
- •Заняття 16. Розв’язання систем тригонометричних рівнянь. Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – відношення тригонометричних функцій.
- •Системи рівнянь, які утримують лише тригонометричні функції.
- •Заняття 17. Рівняння та нерівності, які містять обернені тригонометричні функції.
- •Нерівності, які містять обернені тригонометричні функції.
- •Заняття 18. Контрольна робота №2.
- •Література
Модуль 4. Системи тригонометричних рівнянь. Заняття 15. Розв’язання систем тригонометричних рівнянь.
Системами тригонометричних рівнянь називають системи, які складаються тільки з тригонометричних рівнянь або з тригонометричних і алгебраїчних рівнянь.
Розглянемо деякі види систем тригонометричних рівнянь та методи їх розв’язання.
Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – сума або різниця тригонометричних функцій.
Приклад 15.1. Розв’яжіть систему рівнянь:

Розв’язання.
Перетворимо рівняння
![]() системи:
системи:
 .
.
Враховуючи
рівність
![]() отримаємо :
отримаємо :
 ,
,
 .
.
Розв’язавши
рівняння знайдемо
 ,
тоді
,
тоді
 .
.
Розв’яжемо
разом систему, яка складається з рівнянь
і
![]() :
:

Додавши
і віднявши ці рівняння, отримаємо

 .
Підставляючи значення
в перше рівняння системи знайдемо
.
Підставляючи значення
в перше рівняння системи знайдемо
![]() ,
,
 .
Отже остаточно отримаємо відповідь
.
Отже остаточно отримаємо відповідь

Дану відповідь можна подати у вигляді двох систем:


Приклад 15.2. Розв’яжіть систему рівнянь:

Розв’язання.
З рівняння
випливає:
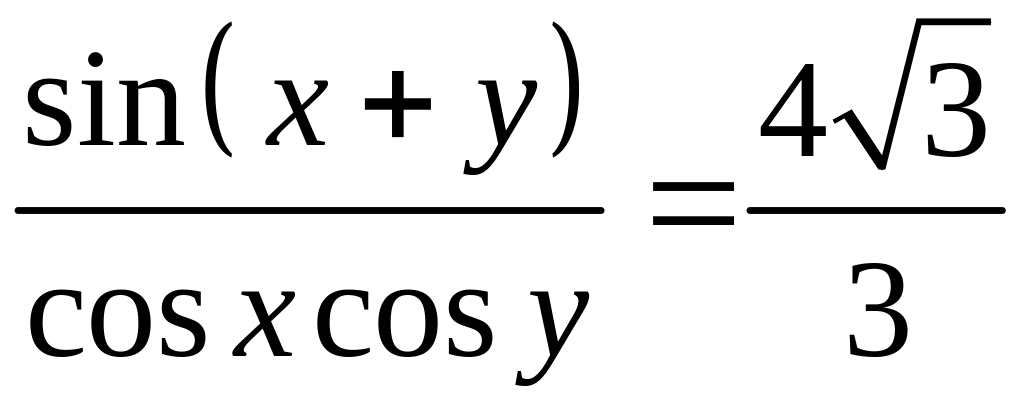 ,
підставивши значення рівності
отримаємо
,
підставивши значення рівності
отримаємо
 ,
звідки
,
звідки
 ,
,
 ,
,
 ,
,
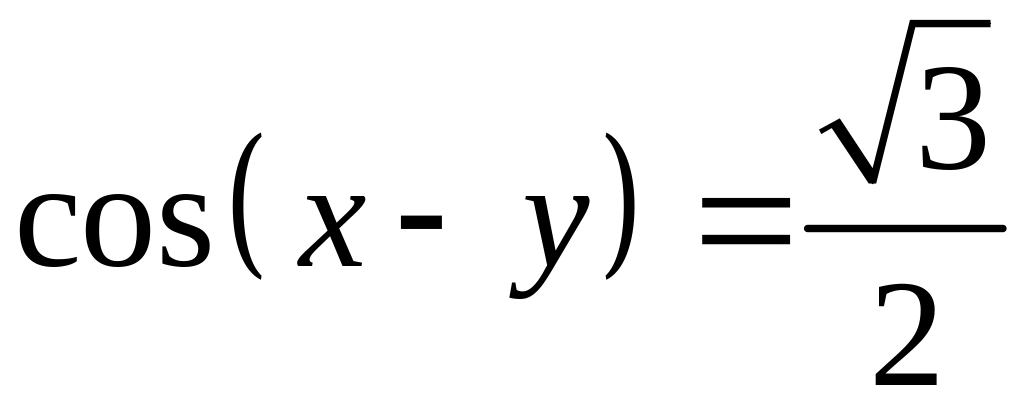 ,
,

Маємо
систему
 додавши і віднявши ці рівняння, отримаємо
загальний розв’язок системи рівнянь:
додавши і віднявши ці рівняння, отримаємо
загальний розв’язок системи рівнянь:

Приклад 15.3. Розв’яжіть систему рівнянь:

Розв’язання.
Ліву частину рівняння
перетворимо в добуток. Матимемо систему


![]()
Розглянемо
різні випадки, які залежать від значення
параметрів
і
![]() .
.
а)
Якщо
 ,
тобто
,
тобто
![]() і
і
 ,
то з першого рівняння системи
дістанемо
,
то з першого рівняння системи
дістанемо
 ,
звідки
,
звідки

Замінимо систему рівносильною системою двох лінійних рівнянь

![]()
Загальним розв’язком системи , а отже і початкової системи буде

б)
Якщо
![]() і
і
![]() або
або
 ,
то система
,
а отже і початкова система несумісні.
,
то система
,
а отже і початкова система несумісні.
в)
і
![]() ,
то система
,
а отже і початкова система невизначені,
тобто мають нескінчену множину розв’язків,
яку можна записати загальною формулою
,
то система
,
а отже і початкова система невизначені,
тобто мають нескінчену множину розв’язків,
яку можна записати загальною формулою
![]() ,
де
довільне число, а
,
де
довільне число, а
![]() .
.
Приклад 15.4. Розв’яжіть систему рівнянь:

Розв’язання. Перетворимо ліву частину рівняння . Отримаємо
![]() ,
,
![]() ,
,
![]() ,
,
 .
.
Врахувавши рівняння системи отримаємо рівняння:
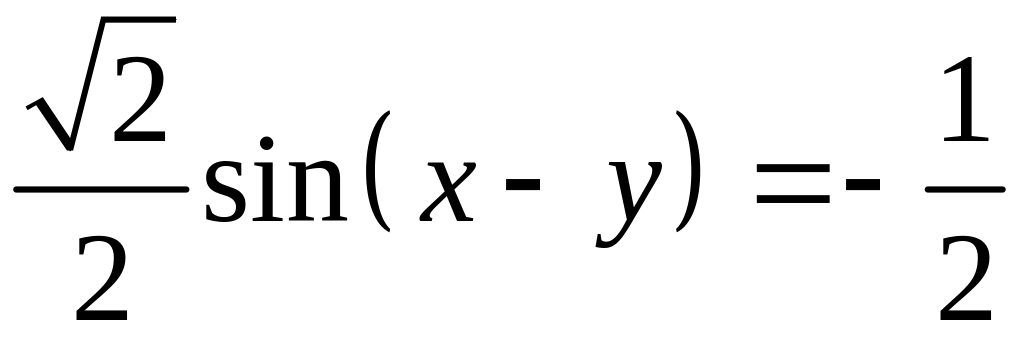 ,
,

 ,
,

Маємо
систему
 додавши
ці рівняння, отримаємо:
додавши
ці рівняння, отримаємо:
 ,
,
 .
.
З
рівняння
системи знайдемо
 .
.
Загальний розв’язок системи:

Системи рівнянь, в яких одне рівняння – алгебраїчне, а друге – добуток тригонометричних функцій.
Приклад 15.5. Розв’яжіть систему рівнянь:

Розв’язання. До першого рівняння системи застосуємо формулу перетворення добутку синусів в суму. Отримаємо:
 ,
,
 ,
,
 ,
,
![]() .
.
Звідси
дістанемо
 додавши і віднявши ці рівняння, отримаємо
загальний розв’язок системи рівнянь:
додавши і віднявши ці рівняння, отримаємо
загальний розв’язок системи рівнянь:

Приклад 15.6. Розв’яжіть систему рівнянь:

Розв’язання. Перетворимо перше рівняння системи. Отримаємо:
 ,
,
![]() ,
,
 ,
,
 ,
,
.
Звідки
 додавши і віднявши ці рівняння, отримаємо
загальний розв’язок системи рівнянь:
додавши і віднявши ці рівняння, отримаємо
загальний розв’язок системи рівнянь:

Приклад 15.7. Розв’яжіть систему рівнянь:

Розв’язання. З першого рівняння виразимо через і підставимо в друге рівняння, де застосуємо формулу додавання аргументів котангенса.
 ,
,
 ,
,
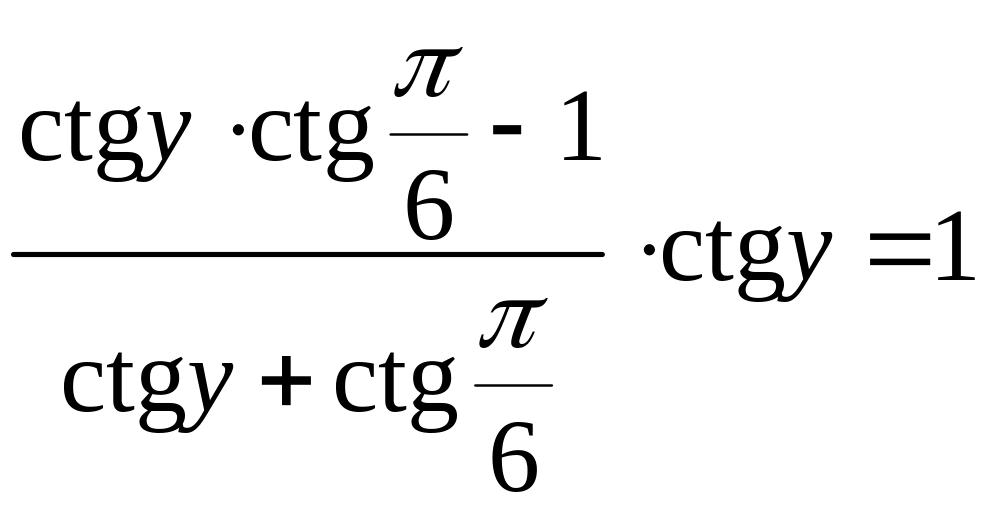 ,
,
 ,
,
![]() ,
,
![]() ,
,


Зауважимо,
що дані серії розв’язків системи можна
об’єднати в одну
 Знайдемо серію розв’язків для змінної
з рівності
,
отримаємо
Знайдемо серію розв’язків для змінної
з рівності
,
отримаємо
 Отже
розв’язком системи буде серія:
Отже
розв’язком системи буде серія:

Завдання для самостійної роботи.
Розв’яжіть систему рівнянь: