Міністерство освіти і науки України

Миколаївський державний університет імені В.О. Сухомлинського

В.Д. Будак, Л.Я. Васильєва, С.В. Ніколаєнко

Елементарна математика.

Тригонометрія.

Навчально-методичний посібник

Миколаїв

2006

УДК 514.116

ББК 22.151.05

Б 90

Книга рекомендована до друку рішенням вченої ради Миколаївського державного університету імені В.О. Сухомлинського.

Протокол №8 від 17.04.06 р.

Рецензенти: завідувач кафедри вищої математики НУК ім. ад-

мірала Макарова, кандидат фіз.-мат. наук, доцент Кузнецов А. М;

доцент кафедри математики МДУ ім. В.О. Сухомлинського Баран О.І.

ЗМІСТ

Передмова .............................................................................................................

Модуль 1. Перетворення тригонометричних виразів.............................

Заняття 1. Загальні відомості з тригонометрії.........................................

Заняття 2. Тотожні перетворення тригонометричних виразів...............

Заняття 3. Тотожні перетворення тригонометричних виразів. Доведення тригонометричних тотожностей.................................................................

Заняття 4. Перетворення тригонометричних виразів в добуток. Доведення умовних тотожностей.......................................................................................

Заняття 5. Тотожні перетворення виразів, що містять обернені тригонометричні функції.

Модуль 2. Розв’язання тригонометричних рівнянь……………………….

Заняття 6. Тригонометричні рівняння.............................................................

Заняття 7. Тригонометричні рівняння II-IV типів..........................................

Заняття 8. Тригонометричні рівняння V-VI типів….......................................

Заняття 9. Рівняння виду ...................................................

Заняття 10. Тригонометричні рівняння VII-VIII типів….................................

Заняття 11. Контрольна робота №1..................................................................

Модуль 3. Тригонометричні нерівності.............................................................

Заняття 12. Розв’язання найпростіших тригонометричних нерівностей.......

Заняття 13. Розв’язання тригонометричних нерівностей методом

інтервалів.................................................................................................................

Заняття 14. Розв’язання тригонометричних нерівностей ..............................

Модуль 4. Системи тригонометричних рівнянь..............................................

Заняття 15. Розв’язання систем тригонометричних рівнянь..........................

Заняття 16. Розв’язання систем тригонометричних рівнянь.........................

Заняття 17. Рівняння та нерівності, що містять обернені

тригонометричні функції.....................................................................................

Заняття 18. Контрольна робота №2................................................................

Література..............................................................................................................

Передмова

Навчально-методичний посібник створено на основі діючої програми з елементарної математики для студентів спеціальності 6.010100 „Педагогіка і методика середньої освіти. Математика”. Його мета – підвищити рівень підготовки студентів, сформувати й розвити математичне мислення, набути практичних навичок з тригонометрії.

Збірник розбито на чотири модуля. Кожен модуль поділено на практичні заняття у відповідності до кількості годин за програмою. Задачі кожної частини розподіляються за методами або типами завдань. Для кожного типу завдань наводиться певна кількість прикладів з детальним розв’язанням. В кінці кожної частини пропонуються приклади для самостійної роботи студентів.

Такий посібник дає можливість студентам ліквідувати прогалини у знаннях і вміннях, розширити та поглибити свої знання, підвищити рівень своєї підготовки. Створений посібник дає можливість викладачу запропонувати таку систему роботи, яка б враховувала диференційований підхід до кожного студента.

Структура посібника дозволяє ефективно використовувати його для роботи за кредитно-модульною системою.

Зміст посібника може бути цікавим при роботі з обдарованими учнями при підготовці до математичних олімпіад.

Модуль 1. Перетворення тригонометричних виразів. Заняття 1. Загальні відомості з тригонометрії.

Тригонометрія (від грецького trigonom- трикутник і metreo- вимірювати)  розділ математики, в якому вивчаються тригонометричні функції, їхні властивості, взаємозв’язки та застосування.

Згадаємо основні факти з тригонометрії.

Значення тригонометричних функцій деяких кутів.

α	0˚	30˚	45˚	60˚	90˚	180˚	270˚	360˚
sin α	0				1	0	-1	0
cos α	1				0	-1	0	1
tg α	0		1		не існує	0	не існує	0
ctg α	не існує		1		0	не існує	0	не існує
sec α	1			2	не існує	-1	не існує	1
cosec α	не існує	2			1	не існує	-1	не існує

Приклад 1.1. Обчисліть .

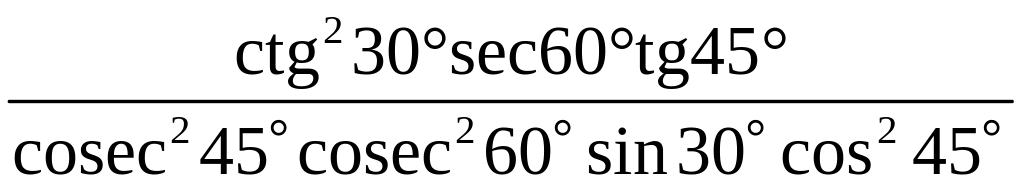Розв’язання.

= = .

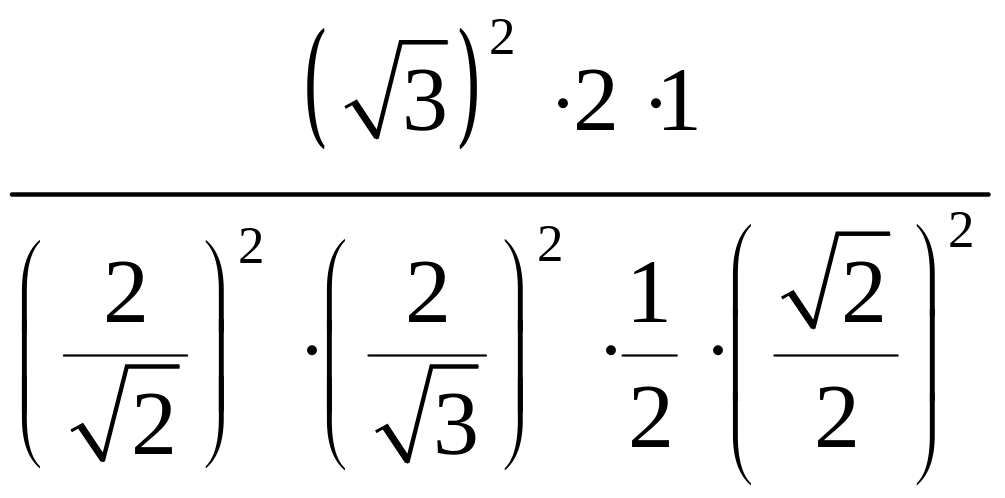Парність та непарність тригонометричних функцій.

Тригонометричні функції , , , і - непарні, а і - парні, тобто

; ;

; ;

; .

Ці формули виконуються для будь-яких значень , при яких функція існує, і дозволяють будь-яку функцію від’ємного аргументу звести до функції з додатнім аргументом.

Приклад 1.2. Обчисліть .

Розв’язання. Враховуючи парність та непарність тригонометричних виразів, отримаємо

= .

Періодичність тригонометричних функцій.

Функція називається періодичною, якщо виконується умова , де . Число - називається періодом функції . Найменший із додатних періодів періодичної функції , якщо він існує, називається її основним періодом.

Тригонометричні функції періодичні, причому , , , мають період , а основним періодом є . Функції і мають період , а основним періодом є .

Приклад 1.3. Звести функції до найменшого додатного аргументу та обчислити їх:

а) .

б) .

Проміжки знакосталості тригонометричних функцій.

П роміжком знакосталості функції називається множина значень аргументу, для яких функція зберігає свій знак, тобто тільки додатна, або тільки від’ємна.

y y y

y

x x x

Синус і косеканс Косинус і секанс Тангенс і котангенс

Формули зведення.

Існує мнемонічне правило, яке дає змогу записати будь-яку формулу зведення:

1) якщо для кута 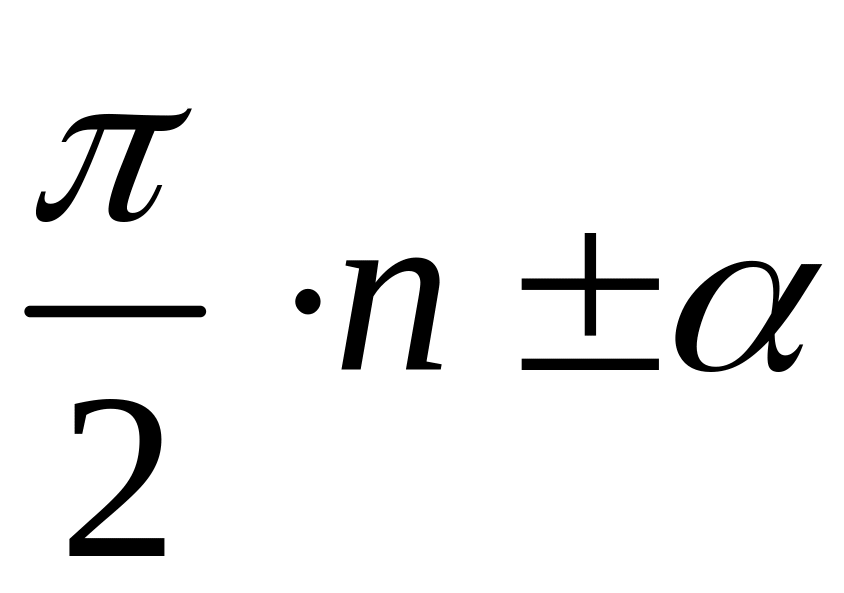(де n N) n непарне, то звідна функція змінює назву на кофункцію ( синус на косинус, тангенс на котангенс і т.д.); якщо n парне, то назва звідної функції зберігається;

2) знак перед зведеною функцією ставиться відповідно до знака звідної функції, при цьому кут α вважається гострим. Якщо звідна функція для кута у даній четверті від’ємна, то функцію гострого кута α множать на -1.

Приклад 1.4. Зведіть тригонометричні функції до аргументу, який належить відрізку :

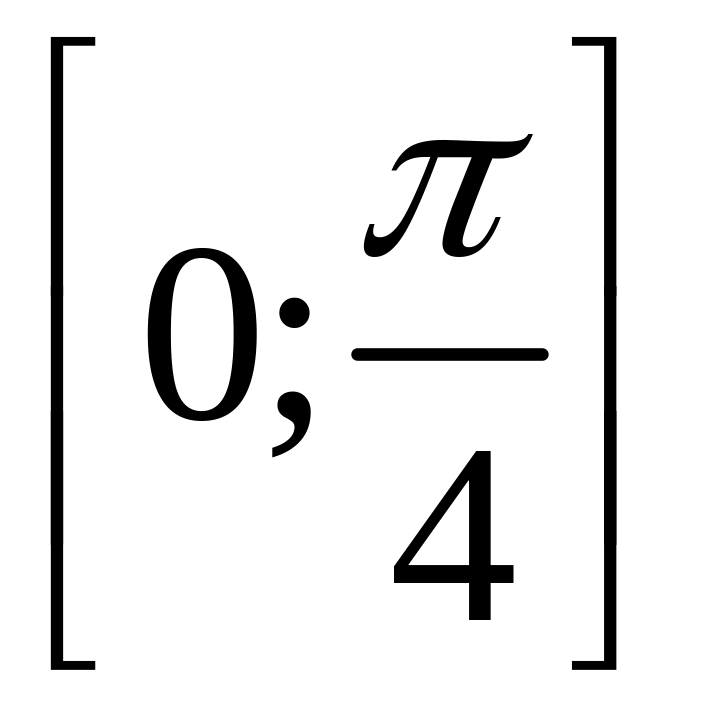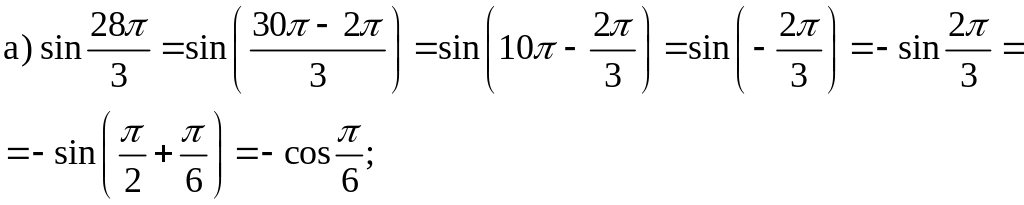
Приклад 1.5. Обчисліть .

Розв’язання.

.
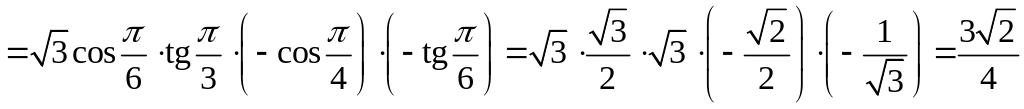