§ 2. Площина у просторі

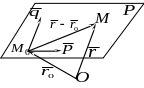
1. Рівняння площини. Нехай у просторі задано прямокутну декартову систему координат і задано точку та вектор . Очевидно, що через точку можна провести єдину площину , перпендикулярну до вектора . Вектор називається нормаллю площини . Знайдемо рівняння площини .

Позначимо через радіус-вектор точки , а через – радіус-вектор змінної точки , яка належить площині . Оскільки координати точки є одночасно координатами її радіуса-вектора, то , . Тоді вектор лежить у площині , тому і взаємно перпендикулярні. Звідси

. (20)

Рівняння (20) називається векторним рівнянням площини .

Враховуючи, що скалярний добуток двох векторів дорівнює сумі добутків однойменних координат цих векторів, то з (20) дістаємо рівняння

, (21)

яке називається рівнянням площини, що проходить через задану точку. Позначивши , з (21) дістаємо загальне рівняння площини

. (22)

Якщо в рівності (22) , то

,

або, після відповідних перепозначень,

. (23)

Це рівняння площини у відрізках. Тут – відрізки, які площина відтинає по осях координат: – по осі абсцис, – по осі ординат і – по осі аплікат.

Площину в просторі можна однозначно задати дещо іншим способом. Нехай площина проходить через точку , паралельно до пари неколінеарних векторів , . Тоді для кожної змінної точки площини вектор можна єдиним чином подати у вигляді лінійної комбінації векторів , :

. (24)

Величини , називаються параметрами, а рівняння (24) називається векторно-параметричним рівнянням площини.

Векторне рівняння (24) рівносильне трьом скалярним рівностям

(25)

які називаються параметричними рівняннями площини.

Оскільки вектори , , компланарні, то

. (26)

Якщо, зокрема, площина проходить через три точки , , , які не лежать на одній прямій, то за можна взяти точку , а за , можна взяти вектори , . Тоді векторна рівність (26) в координатній формі має вигляд

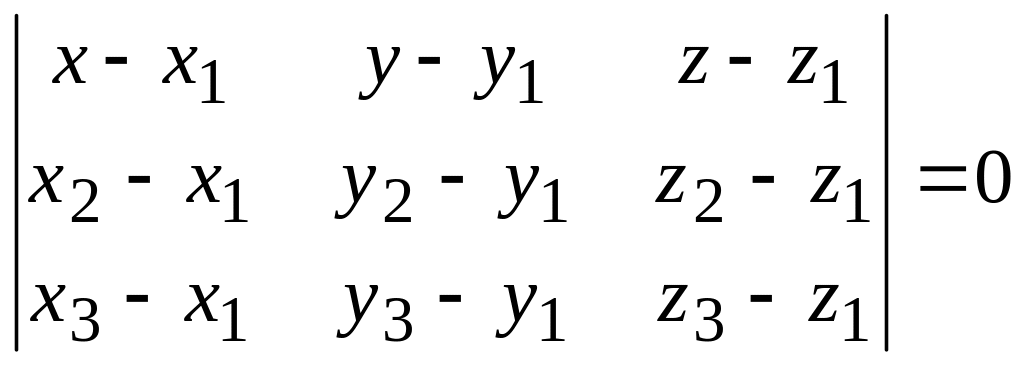. (27)

Це рівняння площини, що проходить через три точки.

2. Кут між двома площинами. Кутом між двома площинами називається кут між їх нормалями. Якщо площини задано загальними рівняннями

,

то нормалі , мають координати , відповідно, тому

.

3. Умова паралельності двох площин. Нагадаємо, що два ненульових вектори , колінеарні тоді і лише тоді, коли їх координати пропорційні. Справді, за теоремою 1 попереднього розділу, вектори та колінеарні тоді і лише тоді, коли існує таке ненульове число , що . Векторна рівність рівносильна трьом скалярним рівностям . Звідси,

. (28)

Нехай дві площини , задано загальними рівняннями

. (29)

Тоді вектори , є нормалями площин , відповідно.

Твердження. Дві площини , паралельні тоді і лише тоді, коли їх нормалі та колінеарні. Звідси, на підставі рівностей (28),

.

4. Умова перпендикулярності двох площин. Дві площини , , задані загальними рівняннями (29), перпендикулярні тоді і лише тоді, коли

. (30)

Справді, площини , перпендикулярні тоді і лише тоді, коли перпендикулярні їх нормалі та . Звідси, , тобто .

5. Нормальне рівняння площини. Векторне рівняння площини

(31)

називається нормальним (нормованим), якщо .

Нехай в рівнянні (31) . Тоді координатами нормалі є її напрямні косинуси, , а рівняння (31) в координатній формі має вигляд

.

Позначивши , отримуємо (скалярне) нормальне рівняння площини

. (32)

Як і у випадку прямої на площині для нормального рівняння площини з двох можливих напрямів нормалі завжди вибирається той, при якому .

Покажемо, що параметр чисельно дорівнює відстані від початку координат до п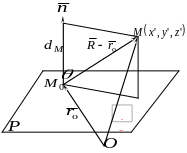 лощини, або, що те саме, довжині перпендикуляра, опущеного з початку координат на площину. Для цього позначимо через площину, задану нормальним векторним рівнянням (31) і розглянемо яку-небудь точку простору, яка не належить площині . Позначимо через радіус-вектор точки , а через позначимо кут між вектором і нормаллю . Підставимо замість в ліву частину рівняння (31) і отриману величину позначимо через :

.

Величина називається відхиленням точки .

За означенням скалярного добутку,

.

Будемо тепер переміщувати точку в просторі, не перетинаючи при цьому площини . Якщо точка лежить у півпросторі, в який спрямовано вектор , то , тому , а отже, і ; у супротивному випадку , отже, , а тому . Таким чином, всі точки, які лежать по один бік від площини, мають відхилення однакових знаків, а точки, які лежать по різні боки від площини, мають відхилення різних знаків.

З рисунка, відстань від точки до площини дорівнює

.

Враховуючи, що

,

остаточно дістаємо

,

тобто відстань від точки до площини дорівнює модулеві результату підстановки координат цієї точки у ліву частину нормального рівняння площини. Зокрема, для початку координат

,

тобто параметр чисельно дорівнює відстані від початку координат до площини.

5. Зведення загального рівняння площини до нормального вигляду. Щоб звести загальне рівняння площини

до нормального вигляду, помножимо обидві частини цього рівняння на ненульовий множник

,

і виберемо так, щоб нормаль мала одиничну довжину. Тоді з умови маємо

.

Звідси,

.

Щоб забезпечити умову , знак завжди вибирається протилежним до знака вільного члена . називається нормувальним множником.