Розділ 3. Прямі та площини

§ 1. Пряма на площині

1. Рівняння лінії на площині. Нехай на площині задано декартову систему координат і деяку лінію . Рівність

(1)

називається рівнянням лінії в заданій системі координат, якщо вона справджується для координат кожної точки лінії і не справджується для координат жодної точки, яка не належить .

Якщо лінію уявляти як траекторію руху точки, то в кожен момент часу відомо положення цієї точки, тобто відомо її координати. Іншими словами, координати точки лінії є функціями часу,

(2)

Рівняння (2) називаються параметричними рівняннями лінії , а змінна називається параметром. Зазначимо, що параметр не обов’язково трактувати як час. Якщо під розуміти координату точки осі , то лінію можна уявляти як образ осі в площині при відображенні (2).

2. Рівняння прямої на площині. Напрямним вектором прямої називається будь-який ненульовий вектор, колінеарний до цієї прямої. Нормальним вектором прямої називається будь-який ненульовий вектор, перпендикулярний до цієї прямої.

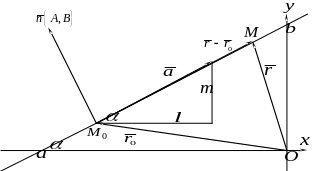
Нехай пряма проходить через точку в напрямі вектора і нехай - радіус-вектор точки , а - радіус-вектор змінної точки прямої. Тоді колінеарний до вектора і, за теоремою 1 попереднього розділу, існує таке число , що

. (3)

Рівняння (3) називається векторно-параметричним рівнянням прямої. Векторна рівність (3) рівносильна парі скалярних рівностей

(4)

З рівностей (4) очевидним чином дістаємо параметричні рівняння прямої

(5)

Поділимо обидві частини першого рівняння системи (4) на , а другого – на і прирівняємо ліві частини. Дістанемо канонічне рівняння прямої

. (6)

Помножимо обидві частини рівняння (6) на і позначимо через . Тоді рівняння (6) набуває вигляду

. (7)

З рисунка видно, що , де - кут, який утворює пряма з додатним напрямом осі абсцис. Величина називається кутовим коефіцієнтом прямої, а рівняння (7) – рівнянням прямої з кутовим коефіцієнтом, що проходить через задану точку.

Розкриємо дужки в рівнянні (7):

.

Позначивши через , отримуємо рівняння прямої з кутовим коефіцієнтом:

. (8)

Геометрично величина означає відрізок, який відтинається прямою (8) по осі ординат. Справді, при з (8) дістаємо .

Якщо пряма проходить через дві точки , , то за напрямний вектор прямої можна взяти вектор , а за точку - точку . Тоді канонічне рівняння (6) набуває вигляду

(9)

і називається рівнянням прямої, що проходить через дві точки.

Нехай - нормальний вектор прямої. Тоді , тому

. (10)

Рівняння (10) називається векторним рівнянням прямої.

Оскільки скалярний добуток двох векторів обчислюється як сума добутків однойменних координат, то рівнянню (10) можна надати такого вигляду

. (11)

Рівняння (11) називається рівнянням прямої, що проходить через задану точку.

Розкривши в рівнянні (11) дужки і позначивши величину – через , дістаємо загальне рівняння прямої

. (12)

Якщо , то з рівняння (12) маємо

.

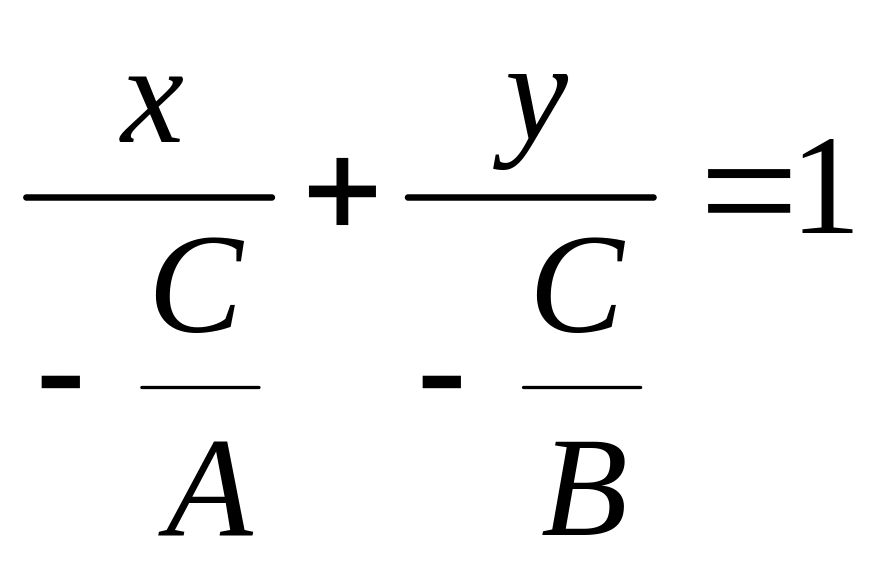Позначивши , , дістаємо рівняння прямої у відрізках

. (13)

Величини геометрично означають відрізки, які відтинаються прямою по осі абсцис та осі ординат відповідно. Справді, при з рівняння (13) маємо ; якщо ж , то .

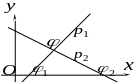3. Кут між двома прямими. Нехай прямі , утворюють з віссю абсцис кути , відповідно. Кутом між прямими , будемо називати будь-який з двох можливих кутів, які утворюють між собою ці прямі, наприклад, кут . Тоді

.

Якщо відомо кутові коефіцієнти , прямих , відповідно, то

. (14)

4. Умови паралельності двох прямих. Зауважимо спочатку, що теоремі 1 попереднього розділу можна надати дещо іншого, зручного для даного пункту, вигляду. Нагадаємо теорему. Два вектори та колінеарні тоді і лише тоді, коли існує таке ненульове число , що . Якщо , , то векторна рівність рівносильна системі скалярних рівностей

Звідси

і тепер теорему можна перефразувати так: два вектори колінеарні тоді і лише тоді, коли їх координати пропорційні.

Твердження 1. Дві прямі , , задані загальними рівняннями , відповідно, паралельні тоді і лише тоді, коли

.

Доведення. Нагадаємо, що коефіцієнти при змінних у загальному рівнянні прямої є координатами нормалі цієї прямої, тому , . Прямі , паралельні тоді і лише тоді, коли їх нормалі , колінеарні. Оскільки два вектори колінеарні тоді і лише тоді, коли їх відповідні координати пропорційні, то

.

Твердження 2. Якщо прямі , задано рівняннями з кутовим коефіцієнтом , відповідно, то прямі , паралельні тоді і лише тоді, коли .

Доведення. Прямі , паралельні тоді і лише тоді, коли кут між ними дорівнює 0, що можливо лише тоді, коли . Тоді з рівності (14) дістаємо, що .

5. Умови перпендикулярності двох прямих. Знайдемо тепер умови перпендикулярності двох прямих.

Твердження 3. Прямі , , задані загальними рівняннями, взаємно перпендикулярні тоді і лише тоді, коли .

Доведення. Прямі , взаємно перпендикулярні тоді і лише тоді, коли взаємно перпендикулярні їх нормалі та , що можливо лише при умові, що , або, що все-одно, .

Твердження 4. Дві прямі , , задані рівняннями з кутовим коефіцієнтом, взаємно перпендикулярні тоді і лише тоді, коли .

Доведення. Прямі , взаємно перпендикулярні тоді і лише тоді, коли кут між ними прямий, , тобто , що, на підставі рівності (14), можливо лише тоді, коли . Звідси, .

6. Жмуток прямих. Множина прямих, які лежать в одній площині і кожна з яких проходить через фіксовану точку , називається жмутком прямих, а точка називається центром жмутка.

Нехай пряма проходить через точку і має рівняння

. (15)

Якщо та вважати змінними параметрами, то (15) задає множину прямих, кожна з яких проходить через точку , тобто (15) задає жмуток з центром у точці . Рівняння (15) називається рівнянням жмутка.

Легко побачити, що жмуток можна визначити парою прямих. Справді, нехай прямі , , визначені загальними рівняннями , відповідно, належать жмуткові з центром у точці . Тоді

.

Звідси, будь-яка пряма з множини прямих, що визначається рівнянням

, (16)

де – довільні числа, проходить через центр жмутка і тому належить жмуткові. Рівняння (16) називається рівнянням жмутка.

Поділимо обидві частини рівняння (16) на і позначимо . Тоді (16) набуде вигляду

. (17)

Рівняння (17) також називається рівнянням жмутка прямих. Від рівняння (16) воно відрізняється тим, що визначає всі прямі жмутка, крім . Незважаючи на це, для розв’язування переважної більшості задач використовується саме рівняння (17).

7. Нормальне рівняння прямої. Векторне рівняння прямої

(18)

називається нормальним (нормованим), якщо .

Нагадаємо, що координатами одиничного вектора є його напрямні косинуси. Звідси, якщо , то , де , – напрямні косинуси нормалі прямої.

Вправа. Перевірити, що якщо , – напрямні косинуси якого-небудь вектора, то .

Враховуючи результат вправи, рівність (18) можна переписати у вигляді

.

Розкриємо дужки і величину позначимо через . Тоді остання рівність набуде вигляду

. (19)

Рівняння (19) називається (скалярним) нормальним рівнянням прямої.

Зазначимо, що з двох можливих напрямів нормалі для нормального рівняння завжди вибирається той напрям, для якого . Справді, якщо нормаль має координати , , то нормаль з протилежним напрямом збігається з вектором , , і має координати , . Якщо величина додатна, то за нормаль прямої береться вектор і тоді ; якщо ж величина від’ємна, то за нормаль прямої береться вектор і тоді .

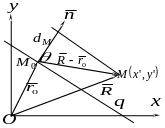З’ясуємо геометричний зміст параметра . Нехай пряму задано нормальним рівнянням. Для довільної точки площини, яка не належить прямій , підставимо її радіус-вектор у ліву частину рівняння (18), а отриману величину назвемо відхиленням точки і позначимо через , так що

.

За означенням скалярного добутку

.

Якщо точку переміщувати на площині, не перетинаючи прямої , то при цьому зберігає знак, оскільки не змінює знака. Звідси, всі точки площини, які лежать по один бік від прямої, мають відхилення однакових знаків, а точки площини, які лежать по різні боки від прямої, мають відхилення протилежних знаків.

З рисунка видно, що відстань від точки до прямої дорівнює

,

або, враховуючи властивість 3⁰ скалярного добутку,

.

З другого боку, враховуючи рівняння (19), маємо

,

так що

.

Зокрема, відстань від початку координат – точки – до прямої дорівнює

.

Таким чином, параметр чисельно дорівнює довжині перпендикуляра, опущеного з початку координат на пряму .

8. Зведення загального рівняння прямої до нормального вигляду. Якщо пряму задано загальним рівнянням

,

то для знаходження її нормального рівняння досить перейти від нормалі до одиничної нормалі . Для цього помножимо рівняння прямої на нормувальний множник такий, щоб дістати одиничну нормаль:

.

З умови маємо

,

звідки

.

Щоб забезпечити умову , знак нормувального множника слід брати протилежним до знака вільного члена .