
Методичка по лабораторной работе №1
.pdf21
Шаг 2.
Строится направляющая –линия проведенная из начала координат под углом 45° Шаг 3.
Линия, соответствующая критерию прямой движется вдоль направляющей от начала координат до касания последней точки, которая и будет решением. В данном случае точка с координатами (0,4; 4,2), т.е. E3
2.3.2 Критерий принятия решений Гермейера
Математическая интерпретация
ZG = max(min(eij q j )) |
|
i |
j |
q j - вероятность условия F1. Если о задаче ничего не известно, то принимаем
q1 = q2 = 0,5
2.3.2.1. Аналитический метод расчета
Дана матрица решений:
|
F1 |
F2 |
E1 |
1 |
1 |
E2 |
3 |
3 |
E3 |
7 |
1 |
E4 |
2 |
2 |
E5 |
3 |
1 |
E6 |
4 |
4 |
E7 |
5 |
1 |
E8 |
4 |
2 |
E9 |
5 |
3 |
E10 |
6 |
2 |
q1 = 0,4 и q2 = 0,6 |
|
|
|
|
|
|
|
Шаг 1. Умножаем каждое ei1 |
на соответствующий ему q j , т.е. |
||||||
|
|
|
|
|
|
|
|
|
|
|
F1 |
F2 |
q1ei1 |
q2ei2 |
|
|
E1 |
|
1 |
1 |
0,4 |
0,6 |
|
|
E2 |
|
3 |
3 |
1,2 |
1,8 |
|
|
E3 |
|
7 |
1 |
2,8 |
0,6 |
|
|
E4 |
|
2 |
2 |
0,8 |
1,2 |
|
|
E5 |
|
3 |
1 |
1,2 |
0,6 |
|
|
E6 |
|
4 |
4 |
1,6 |
2,4 |
|
|
E7 |
|
5 |
1 |
2 |
0,6 |
|
22
E8 |
4 |
2 |
1,6 |
1,2 |
E9 |
5 |
3 |
2 |
1,8 |
E10 |
6 |
2 |
2,4 |
1,2 |
Шаг 2. Выбираем минимум в каждой строке.
|
|
F1 |
F2 |
q1ei1 |
q2ei2 |
min(eij q j ) |
|
|
|
|
|
|
j |
|
E1 |
1 |
1 |
0,4 |
0,6 |
0,4 |
|
E2 |
3 |
3 |
1,2 |
1,8 |
1,2 |
|
E3 |
7 |
1 |
2,8 |
0,6 |
0,6 |
|
E4 |
2 |
2 |
0,8 |
1,2 |
0,8 |
|
E5 |
3 |
1 |
1,2 |
0,6 |
0,6 |
|
E6 |
4 |
4 |
1,6 |
2,4 |
1,6 |
|
E7 |
5 |
1 |
2 |
0,6 |
0,6 |
|
E8 |
4 |
2 |
1,6 |
1,2 |
1,2 |
|
E9 |
5 |
3 |
2 |
1,8 |
1,8 |
|
E10 |
6 |
2 |
2,4 |
1,2 |
1,2 |
|
|
|
|
|
|
1,8 |
Шаг 3. |
|
|
|
|
|
|
Находим максимум в последнем столбце. Оптимальное решение: Все решения
для которых min(eij q j ) максимально. В нашем случае это E9
j
2.3.2.2. Геометрический метод расчета
Геометрическое решение можно найти используя преобразованную плоскость решений.
ei2
4
3
2
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||||||||
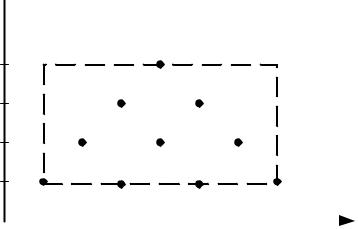
Рис.8 – Исходная плоскость множества решений
23
Решение на плоскости ищется следующим образом: Шаг 1.
Строится новая плоскость решений, где осями будут не ei1 и ei2 , а q1ei1 и q2ei2 . На этой плоскости строятся точки соответствующие решениями.
q2ei2 |
|
|
|
|
|
4 |
|
|
|
|
|
3 |
6 |
|
|
|
|
2 |
|
|
|
|
|
2 |
9 |
|
|
|
|
4 |
8 |
10 |
|
|
|
1 |
5 |
7 |
3 |
|
|
1 |
|
|
|||
|
1 |
2 |
3 |
4 |
q1ei1 |
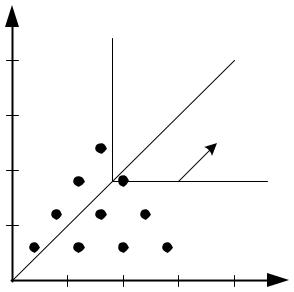
Рис.9 – Новая плоскость множества решений |
|||||
Шаг 2.
Строится направляющая –линия проведенная из начала координат под углом 45°
Шаг 3.
Линия, соответствующая критерию (прямой угол) движется вдоль направляющей от начала координат до касания последней точки, которая и будет решением. В данном случае точка с координатами (2; 1,2), т.е. E9
2.3.3 Критерий произведений
Математическая интерпретация
|
m |
|
Z P = max |
∏eij |
|
i |
j=1 |
|
24
2.3.3.1. Аналитический метод расчета
Дана матрица решений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
F2 |
||
|
|
|
E1 |
1 |
1 |
|
|
|
|
|
E2 |
3 |
3 |
|
|
|
|
|
E3 |
7 |
1 |
|
|
|
|
|
E4 |
2 |
2 |
|
|
|
|
|
E5 |
3 |
1 |
|
|
|
|
|
E6 |
4 |
4 |
|
|
|
|
|
E7 |
5 |
1 |
|
|
|
|
|
E8 |
4 |
2 |
|
|
|
|
|
E9 |
5 |
3 |
|
|
Шаг 1. Находим произведение ei1 |
|
E10 |
6 |
2 |
|
||
|
и ei2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
F1 |
F2 |
|
ei1 ei2 |
|
|
E1 |
|
1 |
1 |
|
1 |
|
|
E2 |
|
3 |
3 |
|
9 |
|
|
E3 |
|
7 |
1 |
|
7 |
|
|
E4 |
|
2 |
2 |
|
4 |
|
|
E5 |
|
3 |
1 |
|
3 |
|
|
E6 |
|
4 |
4 |
|
16 |
|
|
E7 |
|
5 |
1 |
|
5 |
|
|
E8 |
|
4 |
2 |
|
8 |
|
|
E9 |
|
5 |
3 |
|
15 |
|
|
E10 |
|
6 |
2 |
|
12 |
|
Шаг 2. Находим максимум в последнем столбце.
|
F1 |
F2 |
ei1 ei2 |
E1 |
1 |
1 |
1 |
E2 |
3 |
3 |
9 |
E3 |
7 |
1 |
7 |
E4 |
2 |
2 |
4 |
E5 |
3 |
1 |
3 |
E6 |
4 |
4 |
16 |
E7 |
5 |
1 |
5 |
E8 |
4 |
2 |
8 |
E9 |
5 |
3 |
15 |
E10 |
6 |
2 |
12 |
|
|
|
16 |
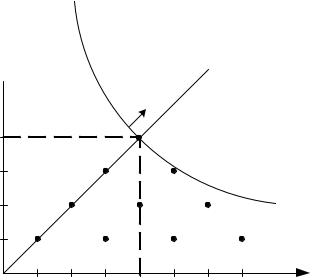
25
Оптимальное решение: Все решения для которых ei1 ei2 максимально. В на-
шем случае это E6
2.3.3.2. Геометрический метод расчета
Геометрическое решение можно найти используя преобразованную плоскость решений.
ei2
4
3
e1 e2 =16
2
1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
ei1 |
Рис.10. – Метод произведений Решение на плоскости ищется следующим образом:
Шаг 1.
Строится новая плоскость решений, где осями будут не ei1 и ei2 , а q1ei1 и q2ei2 . На этой плоскости строятся точки соответствующие решениями.
Шаг 2.
Строится направляющая –линия проведенная из начала координат под углом 45° Шаг 3.
Линия, соответствующая критерию (парабола) движется вдоль направляющей от начала координат до касания последней точки, которая и будет решением. В данном случае точка с координатами (4; 4), т.е. E6
26
3 Контрольные вопросы
1.Что такое критерий принятия решений?
2.В чем состоит особенность критериев Сэвиджа и Байеса-Лапласа?
3.Как осуществляется выбор по критерию геометрически?
4.В каких ситуациях предпочтительнее использовать производные крите-
рии?
5.В каких случаях выбор вариантов решений по критерию Байеса-Лапласа
иХоджа-Лемана совпадет?
4Порядок выполнения работы
4.1Получить задание у преподавателя согласно варианта.
4.2Выполнить задание в соответствии с предложенным вариантом.
а) написать программу, реализующую ввод данных и выбор по соответст-
вующему критерию; б) осуществить выбор по одному из классических критериев: минимакс-
ный, Сэвиджа, оптимистический, Гермейера, произведений, Байеса-Лапласа. Зарисовать полученные результаты;
в) осуществить выбор по одному из производных критериев: Гурвица, Ходжа-Лемана, составному BL(MM). Зарисовать полученные результаты;
г) добавить новые элементы так, чтобы решение по Сэвиджу совпадало с решением по минимаксному критерию;
д) преобразовать матрицу вариантов так, чтобы остались только точки, определяющие границы поля решений и наилучшие решения по минимаксному критерию;
е) определить как изменится решение, если в качестве значений взять значения матрицы с обратным знаком? Записать решения для классических критериев.
4.4 Подготовить и сдать отчет.
27
5 Содержание отчета
Отчет должен содержать:
-вариант задания;
-графические (если возможно) и аналитические результаты
-выводы по результатам проделанной работы.
6 Варианты задания
Вариант 1. Рассмотреть матрицу вариантов решений - Таблица 2. Вариант 2. Рассмотреть матрицу вариантов решений - Таблица 3. Вариант 3. Рассмотреть матрицу вариантов решений - Таблица 4. Вариант 4. Рассмотреть матрицу вариантов решений - Таблица 5. Вариант 5. Рассмотреть матрицу вариантов решений - Таблица 6. Вариант 6. Рассмотреть матрицу вариантов решений - Таблица 7.
Таблица 2
|
F1 |
F2 |
E1 |
3 |
5 |
E2 |
5 |
4 |
E3 |
3 |
4 |
E4 |
4 |
2 |
E5 |
5 |
1 |
|
|
|
E6 |
6 |
4 |
E7 |
7 |
1 |
E8 |
4 |
5 |
E9 |
7 |
4 |
|
|
|
E10 |
4 |
3 |
|
|
|
E11 |
4 |
3 |
|
|
|
E12 |
4 |
3 |
|
|
|
Таблица 3
|
F1 |
F2 |
E1 |
5 |
4 |
E2 |
4 |
3 |
E3 |
4 |
5 |
E4 |
3 |
4 |
E5 |
1 |
7 |
|
|
|
E6 |
4 |
6 |
E7 |
1 |
5 |
E8 |
5 |
3 |
E9 |
3 |
7 |
|
|
|
E10 |
2 |
4 |
|
|
|
E11 |
1 |
6 |
|
|
|
E12 |
4 |
7 |
|
|
|
Таблица 4
|
F1 |
F2 |
E1 |
1 |
3 |
|
|
|
E2 |
3 |
2 |
E3 |
2 |
3 |
E4 |
2 |
5 |
E5 |
4 |
6 |
E6 |
4 |
4 |
|
|
|
E7 |
5 |
3 |
E8 |
4 |
1 |
E9 |
5 |
1 |
E10 |
3 |
6 |
|
|
|
Таблица 6 |
|
|
|
|
|
|
F1 |
F2 |
E1 |
1 |
1 |
|
|
|
E2 |
3 |
3 |
E3 |
7 |
1 |
|
|
|
E4 |
2 |
2 |
E5 |
3 |
1 |
E6 |
4 |
4 |
E7 |
5 |
1 |
|
|
|
E8 |
4 |
2 |
|
|
|
E9 |
5 |
3 |
E10 |
6 |
2 |
|
|
|
Список литературы
28
Таблица 5
|
F1 |
F2 |
E1 |
12 |
3 |
|
|
|
E2 |
3 |
11 |
E3 |
6 |
7 |
E4 |
11 |
5 |
E5 |
4 |
11 |
E6 |
11 |
9 |
|
|
|
E7 |
5 |
8 |
E8 |
4 |
10 |
E9 |
8 |
11 |
E10 |
9 |
6 |
|
|
|
Таблица 7 |
|
|
|
|
|
|
F1 |
F2 |
E1 |
2 |
2 |
|
|
|
E2 |
3 |
4 |
E3 |
5 |
3 |
|
|
|
E4 |
4 |
4 |
E5 |
3 |
9 |
E6 |
8 |
1 |
E7 |
4 |
8 |
|
|
|
E8 |
6 |
3 |
|
|
|
E9 |
5 |
5 |
E10 |
7 |
2 |
|
|
|
1.Мушик Э., Мюллер П. Методы принятия технических решений. –М.:
Мир, 1990.-208с.
29
2.Теория выбора и принятия решений: Учебное пособие. –М.: Наука, Гл.ред. физ.-мат. литературы, 1982.-328 с.
3.Причинный анализ для принятия решений: Учебное пособие/ Л.М.Бакусов, Р.В.Насыров, Е.Г.Лебедев; Уфимск.гос.авиац. техн. ун-т.-Уфа, 1993, 96 с.
4.Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведе-
ние.–М.: Наука, 1970.-707 с.
30
Составитель: Насыров Рашит Вильевич
КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторной работе по курсу "Теория принятия решений"
для бакалавров направления Т28 "Информатика и ВТ" и инженеров специальности 2202
Редактор Г.Р.Орлова ЛБ N 01922 от 16.10.96
Подписано к печати __.__.__. Формат 60x84 1/16. Бумага обёрточная. Печать плоская.
Усл. печ. л. 1,1. Усл. кр.-отт. л. 1,0. Уч.-изд. л. 1,0
Тираж 100 экз. Заказ N ___. Бесплатно.
Уфимский государственный авиационный технический университет Уфимская типография N 2 министерства печати и массовой информации Республики Башкортостан
450000, Уфа-центр, ул.К.Маркса, 12.
