
- •Министерство образования и науки рф фгбоу впо «Вологодский государственный технический университет»
- •Расчетно-графическая работа №5 Расчет и построение электростатического поля двухпроводной линии
- •1.Построение картины поля
- •1.4. Построение картины поля
- •2. Анализ электростатического поля
- •3. Расчет и построение кривой распределения заряда
- •4. Расчет емкости между цилиндрами на единицу длины
Министерство образования и науки рф фгбоу впо «Вологодский государственный технический университет»
Кафедра электротехники
Расчетно-графическая работа №5 Расчет и построение электростатического поля двухпроводной линии
Вариант №1579
Выполнила: студентка.
группа ЭС-32
Проверил: Ганичев Г. Л.
Вологда
2011
Задание на расчет
Раcсчитать и построить электрическое поле двух бесконечно длинных цилиндров кругового сечения с параллельными осями, расположенными в воздухе (рис.1.).
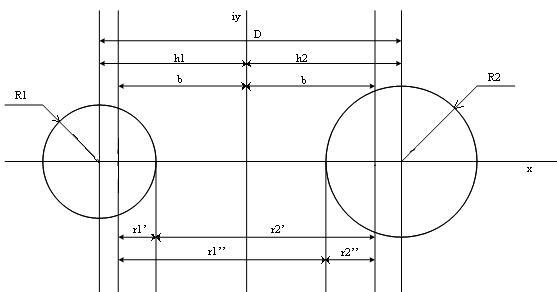
Рис.1
Исходные данные:
-
радиус первого цилиндра, (м);
-
радиус второго цилиндра, (м);
-
расстояние между осями цилиндров, (м);
-
разность потенциалов между цилиндрами,
(В);
-
разность потенциалов между соседними
эквипотенциальными
поверхностями,
(В).![]()
![]()
![]()
![]()
![]()
Задание на расчет
1. Построить картину поля в плоскости, перпендикулярной осям проводников, и нанести на ней линии равного потенциала через интервал приращения потенциала, равный 0,1U0. Построить линии напряженности так, чтобы пересечение линий напряженности с линиями равного потенциала образовывали ячейки близкие к квадрату.
2. Определить максимальное значение напряженности поля в двух случаях:
- расчетным путем;
- приближенно по картине поля.
3. Построить кривую распределения заряда на поверхности цилиндра меньшего радиуса в двух случаях:
- расчетным путем;
- приближенно по картине поля.
4. Произвести расчет емкости между цилиндрами на единицу длины в двух случаях:
- расчетным путем;
- приближенно по картине поля.
1.Построение картины поля
1.1.Расчет расстояний h1 и h2 и определение положения электрических осей
b
=
![]() ,
(1)
,
(1)
где b - расстояние от плоскости нулевого потенциала до электрических осей.
Тогда для цилиндров различного радиуса имеем (рис.1):
![]() =
=![]() =
=![]() (2)
(2)
или (h1+ h2)(h1- h2)=R12 - R22 .
В
рассматриваемом случае b1=b2=b,
т.к. по условию
![]() =
=![]() =
=![]() ,
где
- линейная плотность заряда электрической
оси. С учетом того, что h1
+ h2
= D, после совместного решения получим:
,
где
- линейная плотность заряда электрической
оси. С учетом того, что h1
+ h2
= D, после совместного решения получим:
![]()
(3)
![]()
(4)
Подставив численные значения в (2, 3, 4), получим:
h1=0,078 (м), h2=0,082 (м), b=0.072 (м).
Численные значения h1 и h2 определяют положение геометрических осей цилиндров относительно плоскости нулевого потенциала, совпадающей с осью мнимых чисел y на комплексной плоскости, а численное значение величины b - положение электрических осей (рис. 1).
1.2. Расчет линий равного потенциала
Как известно, уравнением линии равного потенциала является уравнение окружности с радиусом:
R=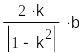
и координатами центра окружности:
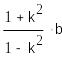
![]()
x0= , y0=0 , здесь k= .
где r2 - расстояние от электрической оси, расположенной справа от оси y до произвольной
точки на линии равного потенциала;
r1 – то же самое, но для электрической оси, расположенной слева от оси y.
Таким образом, если найдено значение k, то для каждой линии равного потенциала легко могут быть вычислены x0y и радиус R0y , где y-порядковый номер линии.
Пусть U0 - заданная разность потенциалов между цилиндрами, тогда:
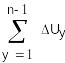
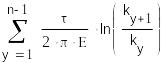
![]()
![]()
= = = ,
где n=11 – число эквипотенциальных линий,
![]()
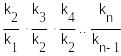 =
. Тогда B=
=
. Тогда B=![]()
![]()
П![]()
![]() ри
условии, что ΔU=const, имеем =
ри
условии, что ΔU=const, имеем =
В нашем случае (см. рис.1):
![]()
![]()
kn= , .
Как следует из рис.1:
![]()
![]() =
0.024 (м), = 0,12 (м), k1=4,987,
=
0.024 (м), = 0,12 (м), k1=4,987,
![]()
![]() =
0,03 (м), = 0,114 (м), k11=0,26.
=
0,03 (м), = 0,114 (м), k11=0,26.
С учетом вышесказанного определим B:
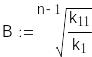
![]()
Определим радиусы и координаты центра эквивалентных окружностей:
Таблица 1
y |
ky |
Ry= , (м)
|
x0y= , (м) |
1 |
4.987 |
0.03 |
-0.078 |
2 |
3.711 |
0.042 |
-0.083 |
3 |
2.762 |
0.06 |
-0.093 |
4 |
2.055 |
0.092 |
-0.116 |
5 |
1.529 |
0.164 |
-0.179 |
6 |
1.138 |
0.553 |
-0.558 |
7 |
0.847 |
0.43 |
0.436 |
8 |
0.63 |
0.15 |
0.166 |
9 |
0.469 |
0.086 |
0.112 |
10 |
0.349 |
0.057 |
0.092 |
11 |
0.26 |
0.04 |
0.082 |
1.3.Расчет линий напряженности поля
Уравнение любой линии напряженности поля является уравнением дуги окружности, пересекающейся с электрическими осями, с координатами центра:
![]()
x0=0, yo=
Линии напряженности поля должны быть построены так, чтобы весь поток вектора напряженности E был поделен ими на равное целое число трубок. Для этого необходимо при переходе от любой линии напряженности поля к соседней изменить угол на постоянную величину.
Вычислим величину Δb:
з![]() а
начальную линию напряженности поля
примем линию, соединяющую электрические
оси. Угол b для нее равен град.
Вторую линию строим таким образом, чтобы
в результате пересечения обеих линий
с эквипотенциальными линиями получался
квадрат. Соединяя любую точку отрезка
второй линии, являющейся верхней стороной
квадрата, с электрическими осями, находим
угол и вычисляем Δb:
а
начальную линию напряженности поля
примем линию, соединяющую электрические
оси. Угол b для нее равен град.
Вторую линию строим таким образом, чтобы
в результате пересечения обеих линий
с эквипотенциальными линиями получался
квадрат. Соединяя любую точку отрезка
второй линии, являющейся верхней стороной
квадрата, с электрическими осями, находим
угол и вычисляем Δb:
![]()
![]()
![]()
Поскольку диапазон изменения угла равен 360, то число линий напряженности поля определяется из условия:
![]()
![]()
Полученный
результат округляем до ближайшего
целого четного числа
![]() .
После этого уточняется величина Δb:
.
После этого уточняется величина Δb:
![]()
![]()
![]()
Координаты центра окружности и радиус окружности вычисляются с помощью выражений:
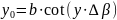 -
координата центра окружности,
-
координата центра окружности,
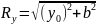 – радиус
окружности,
– радиус
окружности,
где y – порядковый номер окружности.
Результаты расчета представлены в таблице 2.
Таблица 2
y |
Βy |
Yo,y , м |
Ry ,м |
0 |
0,00 |
∞ |
∞ |
1 |
40685,00 |
0.173 |
0.188 |
2 |
45,00 |
0.072 |
0.102 |
3 |
67.5 |
0.03 |
0.078 |
4 |
90,00 |
0,00 |
0.072 |
5 |
112.5 |
-0.03 |
0.078 |
6 |
135,00 |
-0.072 |
0.102 |
7 |
157.5 |
-0.173 |
0.188 |
8 |
180,00 |
∞ |
∞ |
