Лекции по ОТН / Лекции

За ∆t объект в (1) останется в этом состоянии с вероятностью р11 или перейдет в (2) с вероятностью р12 или в (3) с вероятностью р13.

Вероятности р11… и т.д. могут быть подчинены любому закону.

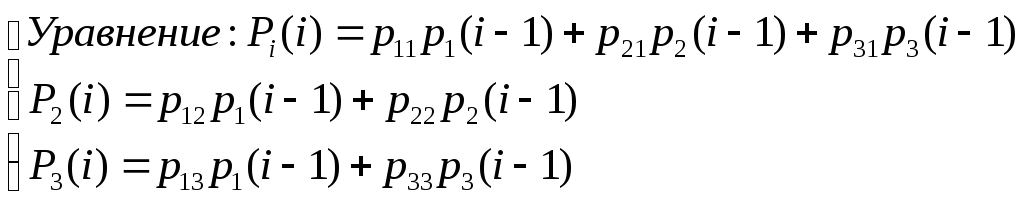
По этой системе уравнений можно найти вероятность нахождения системы в каждом из состояний.

,

M(0)-матрица – строка начального состояния

M(0)=| P₁(0) P₂(0) P₃(0) |

| 1 0 0 | - скорее всего

M=|квадратная матрица переходов в объекте| =

1_i 2_i 3_i

Д=|матрица столбец искомого состояния| =

Определим вероятность нах-я объекта после 2-х шагов во (2). Считаем, что p₁₃=0 (p₃₃=0)

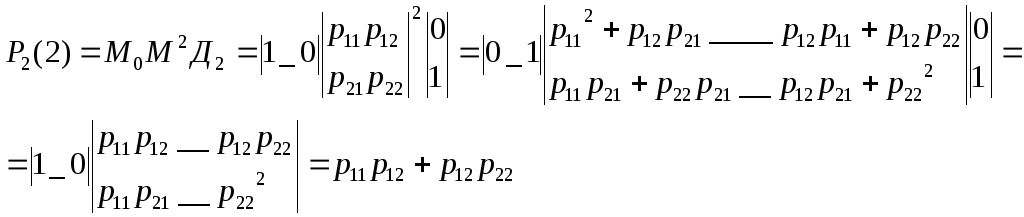
Вывод: метод пригоден для объектов с малым числом состояний и элементов, или с помощью ЭВМ. Метод исп-ся при статическом моделировании надежности. Используется при составлении диагностических тестов на основе дерева отказов.

Метод переходных интенсивностей.

Используется: 1) при экспоненциальном законе распределения времени безотказной работы и времени восстановления.

2) потоки отказов и потоки восстановлений стац-е и без последействия (простейшие)

3) время работы непрерывное.

Надежность таких объектов описывается системой дифференциальных уравнений 1-го порядка.

Пример: рассмотрим объект, который может находится в 2-х состояниях.

Отказ 0 P₀(t)=e^-λt λ-параметр потока отказов(интенсивность отказов)

Восст-е 1 P₁(t)=e^-μt μ-параметр потока восст-ий(интенсивность восст-я)

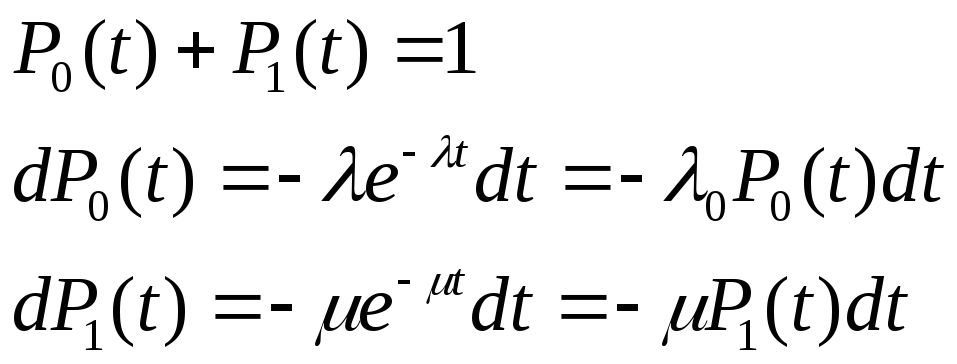
Число диф-х ур-ий равно числу состояний объекта. Найдем вероятность пребывания объекта в каждом (t+dt)

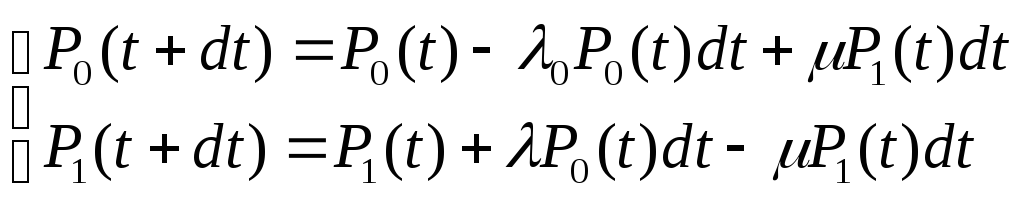
Преобразуем данное ур-е: 1. перенесем из правой части в левую

и

2. Разделим обе части на dt:

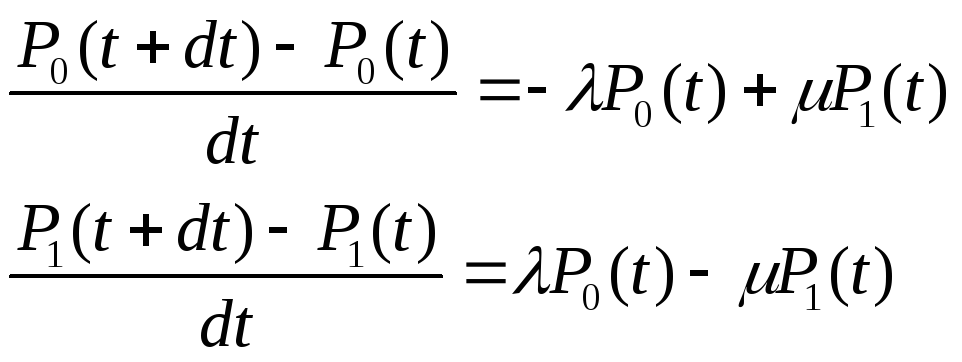
3. Перепишем левую часть:

Ур-я Колмогорова-Чемплена

Эти ур-я позволяют определить вероятность нах-я системы в любом из состояний. Для составления ур-ий нужно составить граф состояний объекта, вершины которого = сост-я, а ребра = направление переходов из состояния в состояние.

При составлении ур-ий все входящие ребра учитываются со знаком «+», а выходящие со знаком «-».

С исп-м системы диф-х ур-ий находят:

1. вероятность нахождения объекта в любом состоянии

2. ф-ии готовности и ф-ии простоя. Ф-ия готовности опр-ся суммой вероятностей работоспособных состояний:

n – число раб-х состояний

Ф-ия простоя равна сумме вероятностей нераб-х состояний:

z – число нераб-х состояний.

3. коэф-ты готовности и простоя.

Коэф-т готовности:

Коэф-т простоя: .

Для нахождения данных показ-й исп-ся следующие уравнения: 1. Решение системы диф-ых ур-ий.

2. Перейти из временной области в опер-ю система алгебраических уравнений.

3. Все процессы в объекте считаются установившимися. . Вер-ти состояний объекта наз-ся финальными или предельными и от t не зависят. Система диф-ых уравнений => в систему алг-их уравнений.

Найдем для объекта с 2 сост-ми K_Г и K_п:

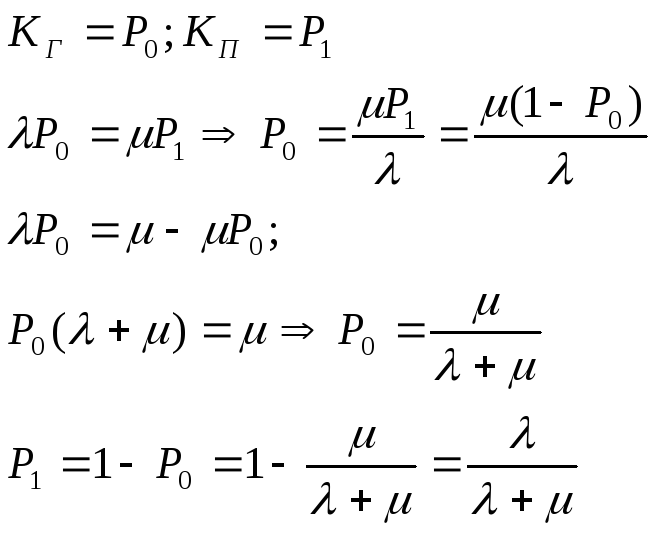
Лекция 9.

Применение метода переходных интенсивностей для расчета надежности.

Соединение такого вида имеет две модели поведения:

1. после отказа любого из элементов система отказывает и исправные элементы отключаются, а неисправные восстанавливаются. После восстановления неисправный элемент включае6тся в систему и поэтому система функционирует.

2. после отказа любого элемента систма отказывает, отказавший элемент ставиться на восстановление, все остальные продолжают функционировать и они могут отказать.

Число неисправных элементов может быть люьым до n. Возможно три модификации:

1. неограниченное восстановление. На восстановление может находиться любое число элементов, n – число элементов, m – число ремонтных мест.

2. частично ограниченное восстановление, когда m<n.

3. послностью ограниченное восстановление, m=1.

Расмторим следующию модель.

Число состояний n+1.

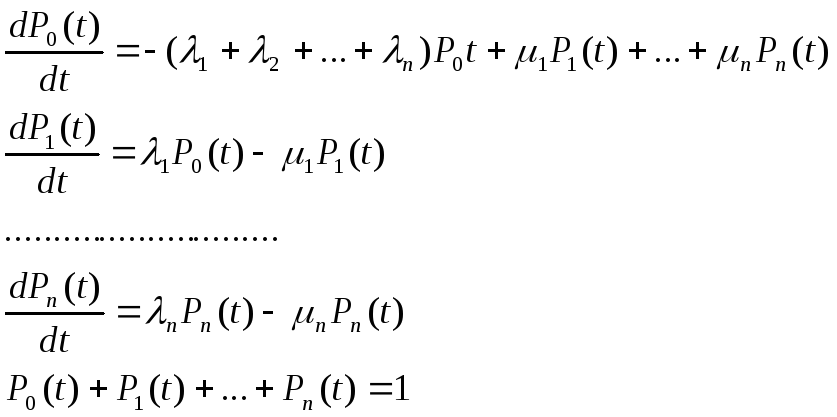
По уровнениям можно найти К_Г и К_П. Для нахождения К_Г перейдем к финальным вероятностям:

Используя метод подстановки получим выражение:

.

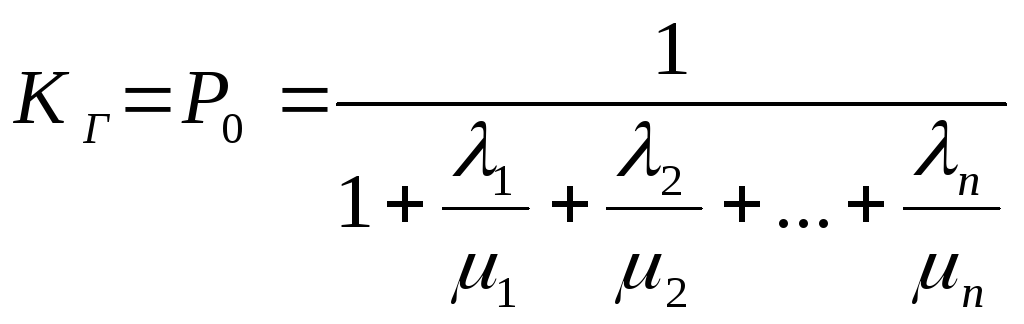Применеие метода переходных интенсивностей для резервного соеденения.

n=k+1;r=1.

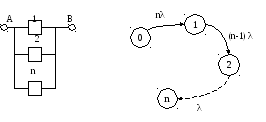
Граф такого вида (однонаправленный, неветвящийся) называется схемой «Гибели».

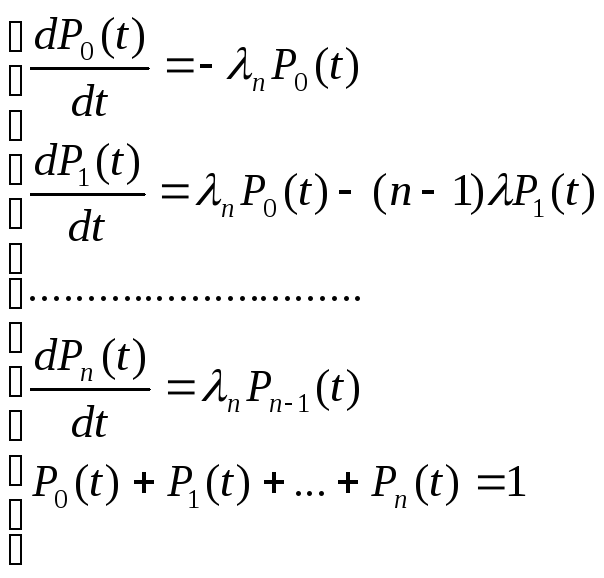
Система урвнений для нахождения К_Г и К_П решается в операторной области:

Рассмотрим резервное постоянное общее с дробной кратностью. . В графе нерабочее состояние наступит когда интенсивность перехода равна rλ.

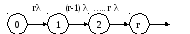
Применеие метода переходных интенсивностей к резервированию замещением.

Резервируемый элемент может работать в трех режимах:

1. Горячий режим. Рис 5. 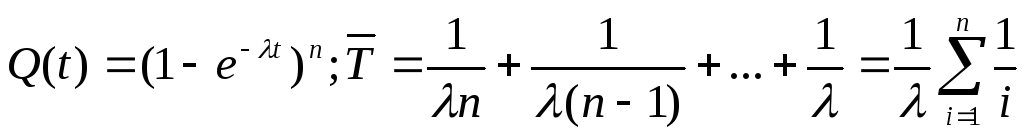. Вывод: горячие резервирование замещением полностью совпадает по описанию с постоянным общим резервированием.

2. Холодный режим. Если элементов n, то состояние все равно n+1. – граф схемы гибели.

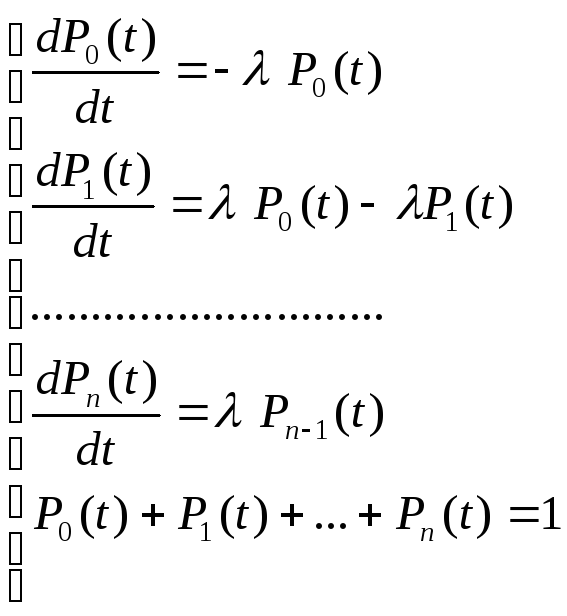
Результат:

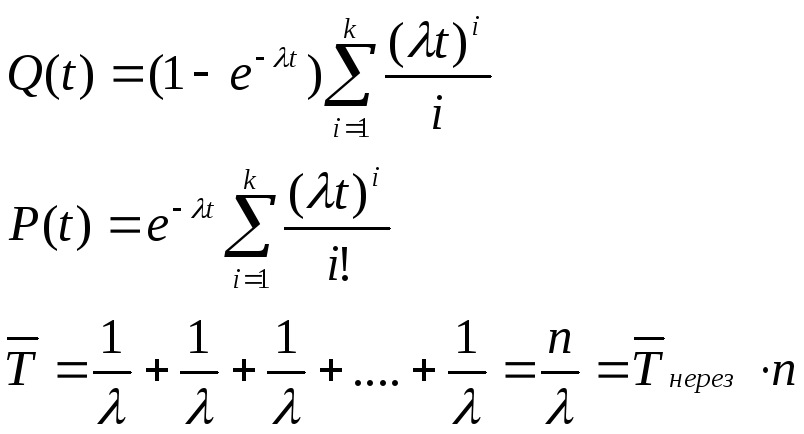
В случае резервирования без восстановления граф равен схеме «гибели».

Применение метода переходных интенсивностей для резервируемых систем с востанавлеемыми элементами.

k=1;n=2. Элементы в объекте однотипны; имеются интенсивность отказов λ и интенсивность восстановления μ.

В системе введен контроль состояний элементов. Контроль идеальный: отказавший элемент обноруживается после отказа и становиться на восстановление. Схема «гибили» и «размножения» -

Интенсивности М₁ и М₂ определяются стратегий восстановления:

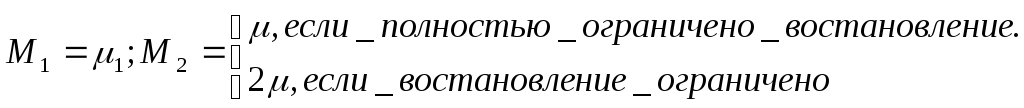
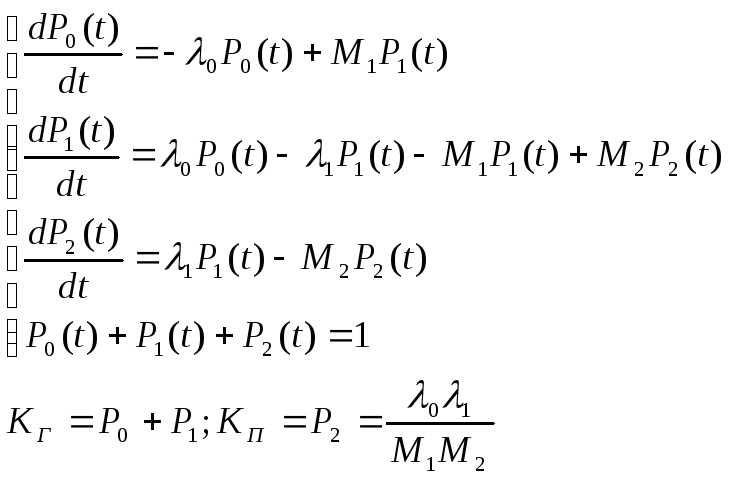
Поэлементное резервирование замещением и востанавлемыми элементами.

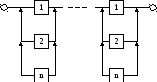
Расчет поэлементного резервирования ведется по формулам общего резервирования:

P_p(t)= P₁(t) P₂(t)… P_m(t).

Каждая из m вероятностей ищеться отдельно.

ЛИСТ №7

Вывод: Выигрыш средней наработки до отказа при пост. общем резервировании снижается по мере роста кратности резерва( показателя к). Введение 1-го резервного эл-та увеличивает нагрузку на 50%; 2-го на 22%.

Поэлементное резервирование с целой кратностью.

r=1 n=k+1

Показатели надежности при поэлементном резервировании рассчитывается по формулам пост. общего резервирования.

Все элементы в объекте равнонадежны, тогда , k – кратность резервирования.

Сравним общее поэлементное резервирование и найдем выигрыш по вероятности отказа.

, m – глубина резервирования.

Выигрыш от введения поэлементного резерва зависимости от m и k.

Надежность переключающихся устройств и ее влияние на качество резервирования.

При общем резервировании на выходе объекта (). Ост-е( резервирование) находится в рабочем состоянии и подключается поле того как сдох 1. Для переключения ставится спец-е переключающее устройство ( имеет конечную над-ть) -> влияет на состояние схемы. Отказы переключ-х усройств: ложное замыкание, размыкание при отсутствии отказа и т.д.

Две схемы:

А) - коэффициент ненад-ти.

λ λ_пу λ_пу<< λ₀

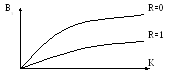
График зависимости В средней () от R и К.

В тем больше, чем надежнее переключ. устр-во(ПУ) и выше к.

При молонадежных ПУ увеличение к не приводит к увеличению надежности.

К=1 λ_пу<<λ₀

K=5 λ_пу==λ₀

Постоянное общее резервирование с дробной к.

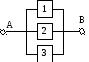
К=(n-r)/r; , i – число отказавших эл-ов

(n-r) – число резервных эл-ов.

С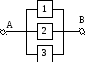редняя наработка:

Пример. При отказе любого эл-та из 3-х в объекте сохранится рабочее состояние. При отказе 2-х элементов – объект нерабочий.

Решение: r=2 n=3 k=(n-r)/r=(3-2)/2=0.5

B_Q=Q_н(t)/Q_p(t); Q_H=1-P_H(t)

Мажоритарное резервирование

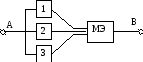- это вид пост. общего резервирования с дробной кратностью.

в структуру включено n – нечетных эл-ов. Сигналы подаются на вход МЭ( мажоритарного эл-та).